Треугольник – одна из самых основных и фундаментальных геометрических фигур, которая имеет огромное значение в математике и геометрии. Определение треугольника является хорошим стартом для изучения этих наук. Треугольник – это фигура, состоящая из трех сторон и трех углов.
Треугольник является важным объектом изучения в математике. Он играет ключевую роль в геометрии и алгебре. Свойства треугольника занимают важное место в теории чисел и тригонометрии. Треугольники присутствуют во многих математических моделях и применяются в различных областях науки.
Геометрическая форма треугольника имеет множество особенностей и свойств, которые изучаются математиками в течение многих лет. Она также служит основой для доказательства многих других теорем и утверждений. Треугольники могут быть равносторонними, равнобедренными или разносторонними, и каждый из этих типов треугольников имеет свои характеристики и свойства.
Роль треугольника в геометрии и математике
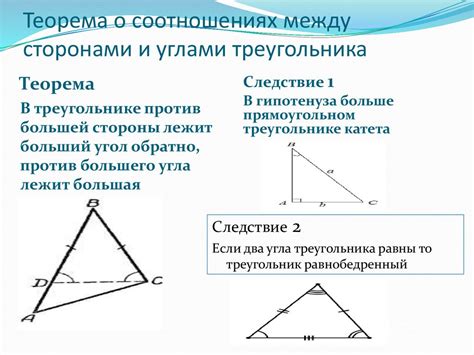
В геометрии треугольник является простейшей фигурой, состоящей из трех отрезков, называемых сторонами, и трех углов, образованных этими сторонами. Он обладает базовыми свойствами, такими как сумма углов треугольника, равенство двух сторон и углов, медианы, биссектрисы и высоты треугольника.
Треугольник также играет важнейшую роль в математике, особенно в геометрии. Он является основой для многих теорем, в том числе теоремы Пифагора, теоремы синусов и косинусов. Треугольник позволяет нам решать различные задачи, такие как нахождение площади, периметра, высоты, радиуса вписанной и описанной окружности.
Более того, треугольник используется в различных областях науки и техники. Он является основой для построения геометрических моделей, триангуляции, построения треугольников Делоне и Вороного. Треугольники также используются в компьютерной графике, алгоритмах расчета и других приложениях, связанных с геометрией и математикой.
Таким образом, треугольник играет ключевую роль в геометрии и математике. Он обладает множеством свойств и особенностей, которые помогают нам понять и описать окружающий нас мир. Без треугольника мы не смогли бы развивать геометрию и математику так, как это делается сегодня.
Значение треугольника в геометрии
Треугольники могут быть различными по форме и по размеру. Существуют острые, тупые, прямоугольные и разносторонние треугольники. Кроме того, у треугольников существуют различные свойства и теоремы, которые позволяют решать различные задачи.
Значение треугольника в геометрии заключается в том, что он является основным строительным блоком для многих других фигур. Например, многогранники состоят из треугольников, а также геометрические фигуры, такие как круги и эллипсы, могут быть приближены с помощью треугольников.
Треугольники также важны для решения геометрических задач. Благодаря своим свойствам, треугольники позволяют находить длины сторон, измерять углы, определять площадь и периметр фигур, а также решать различные треугольные теоремы.
Важно понимать, что треугольник был изучен древними математиками и философами, и его значение с тех пор не утратило своей актуальности. С помощью треугольников мы можем понять и объяснить множество закономерностей и явлений в геометрии и математике в целом.
Доказательство свойств треугольника
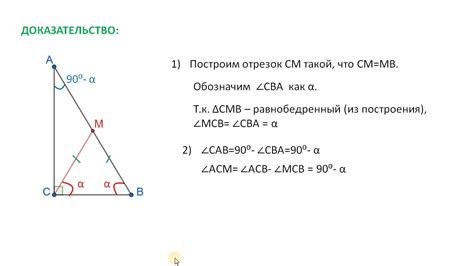
1. Сумма углов треугольника равна 180 градусам.
Для доказательства этого свойства можно воспользоваться следующей логикой:
Пусть у нас есть треугольник ABC.
Доказательство:
1) Построим прямую, проходящую через точку B и параллельную стороне AC треугольника.
2) Обозначим точку пересечения этой прямой с продолжением стороны AB через D.
3) Так как угол между прямыми, определяемыми сторонами AB и AC, равен углу между прямыми, определяемыми сторонами AB и BD, то угол A равен углу D.
4) Следовательно, сумма углов A и D равна 180 градусам.
5) Но угол A равен углу D, так как они являются вертикальными.
6) Следовательно, сумма углов треугольника ABC равна 180 градусам.
2. Неравенство треугольника.
Для доказательства неравенства треугольника можно воспользоваться следующей логикой:
Пусть у нас есть треугольник ABC.
Доказательство:
1) Рассмотрим отрезки AB, BC и AC.
2) Сумма двух из них всегда больше третьего, то есть AB + BC > AC, AC + BC > AB и AB + AC > BC.
3) Если данное неравенство не выполняется, то треугольник не может существовать.
4) Следовательно, неравенство треугольника верно.
3. Сходство треугольников.
Для доказательства сходства треугольников можно воспользоваться следующей логикой:
Пусть у нас есть два треугольника ABC и DEF.
Доказательство:
1) Построим такие две прямые, проходящие через вершины треугольников, чтобы они были параллельны.
2) Получим три пары подобных треугольников: ABF и ABE, BCF и BCE, ACF и ACE.
3) По свойству подобных треугольников, отношение соответствующих сторон их равно.
4) Поэтому, треугольники ABC и DEF подобны.
Таким образом, эти свойства треугольника являются основополагающими для геометрии и математики, и использование их позволяет доказывать различные утверждения и теоремы в этой области.
Треугольник как основной элемент геометрических фигур
Треугольник может быть различных видов в зависимости от свойств его сторон и углов. Одна из классификаций основана на длинах сторон: треугольник может быть равносторонним (все стороны равны), равнобедренным (две стороны равны) или разносторонним (все стороны разные).
Другая классификация основана на величине углов треугольника: треугольник может быть прямоугольным (один из углов равен 90 градусам), остроугольным (все углы меньше 90 градусов) или тупоугольным (один из углов больше 90 градусов).
Треугольники также играют важную роль в других областях математики и физики. Например, их свойства используются при решении проблем, связанных с расчетами площади, периметра, высоты, медиан и других величин, связанных с треугольниками. Кроме того, треугольники имеют важное значение в тригонометрии, где они используются для определения и измерения углов и сторон треугольников.
Использование треугольника в практике
Треугольники широко используются в практике и играют важную роль в различных областях, включая геометрию, физику, строительство и компьютерную графику.
В геометрии треугольники являются основными фигурами. Они используются для изучения пропорций, углов и длин сторон, а также для решения задач, связанных с площадью, периметром и теоремами треугольника. Треугольники также играют важную роль в трехмерной геометрии, где они используются для построения и анализа сложных многогранных фигур.
В физике треугольники используются для решения задач, связанных с различными аспектами движения и силы. Например, треугольники используются для расчета углов между силами, определения направления векторов и нахождения составляющих силы в различных направлениях. Треугольники также используются для расчета траекторий движения и определения сил трения.
В строительстве треугольники используются для измерения углов и прямых линий, а также для строительства фундаментов и каркасов зданий. Они используются для создания треугольных призм и пирамид, которые имеют прочную и стабильную структуру. Треугольники также используются для определения высоты зданий и расчета объема материалов.
В компьютерной графике треугольники широко используются для отображения и обработки графических изображений. Они играют важную роль в растровой и векторной графике, где они являются основными элементами для создания форм и фигур. Треугольники используются для заполнения, преобразования и трехмерного отображения графических объектов.
Теоремы о треугольнике и их применение
В геометрии и математике существует несколько важных теорем о треугольниках, которые имеют широкое применение при решении различных задач. Рассмотрим некоторые из них.
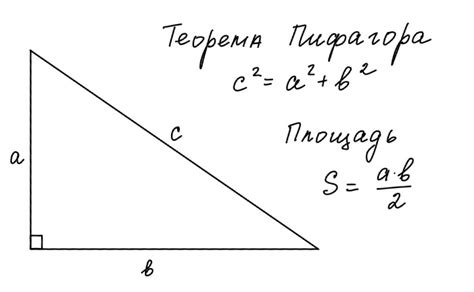
Теорема Пифагора
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула герона
Формула герона позволяет вычислить площадь треугольника по длинам его сторон. Она гласит, что площадь равна половине произведения длин всех его сторон и квадрату полупериметра.
Теорема синусов и косинусов
Теорема синусов устанавливает соотношение между длинами сторон треугольника и синусами соответствующих ему углов. Теорема косинусов позволяет выразить косинус угла треугольника через длины его сторон.
Эти теоремы находят применение при решении различных задач, например, при нахождении длин сторон и углов треугольника, определении его типа (равносторонний, равнобедренный, прямоугольный), а также при вычислении площади треугольника и его высот.
Решение задач с использованием треугольника
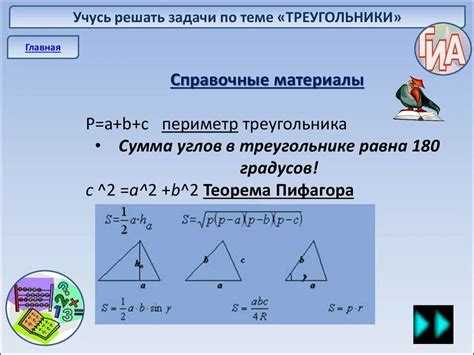
- Вычисление площади треугольника происходит по формуле: S = 0.5 * a * h, где a - основание треугольника, h - высота, проведенная к основанию. Это позволяет находить площадь треугольников разных форм и размеров.
- Теорема Пифагора (a^2 + b^2 = c^2) позволяет рассчитывать длину стороны треугольника, если известны длины двух других сторон. Таким образом, можно решать задачи на нахождение длины стороны треугольника или проверять, является ли треугольник прямоугольным.
- Треугольник может служить основой для решения задач на углы. Например, если известны две стороны треугольника и угол между ними, можно использовать закон синусов (a/sinA = b/sinB = c/sinC) или закон косинусов (c^2 = a^2 + b^2 - 2ab*cosC) для нахождения длин других сторон или углов треугольника.
Также треугольник может быть использован в решении задач на аналитическую геометрию, например, для нахождения координат вершин треугольника, если известны координаты одной или двух вершин и другие условия.
Благодаря разнообразию свойств и формул, связанных с треугольником, он играет важную роль в геометрии и математике, помогая решать различные задачи и строить новые математические модели.
Разнообразие видов треугольников
В геометрии существует большое разнообразие видов треугольников, которые отличаются по длинам сторон и углам. Некоторые из наиболее известных видов треугольников:
- Равносторонний треугольник. Все его стороны равны друг другу. Углы в равностороннем треугольнике равны 60 градусам.
- Равнобедренный треугольник. В нем две стороны равны друг другу. Углы при основании равны.
- Прямоугольный треугольник. В нем один из углов является прямым (равным 90 градусам).
- Остроугольный треугольник. Все его углы острые (меньше 90 градусов).
- Тупоугольный треугольник. Один из его углов тупой, то есть больше 90 градусов.
Это только некоторые из самых известных видов треугольников. В геометрии есть и другие разновидности треугольников, которые могут иметь различные комбинации длин сторон и углов. Каждый из этих видов треугольников имеет свои свойства и особенности, которые изучаются в математике.
Связь треугольника с другими фигурами

| Фигура | Описание связи |
|---|---|
| Прямоугольник | Треугольник может быть половиной прямоугольника, если его основание является одной из сторон прямоугольника. |
| Параллелограмм | Треугольник может быть половиной параллелограмма, если его основание является одной из сторон параллелограмма. |
| Трапеция | Треугольник может быть половиной трапеции, если его основание является одной из сторон трапеции. |
| Ромб | Треугольник может быть половиной ромба, если его высота является одной из сторон ромба. |
| Вписанная окружность | Внутренняя окружность, касающаяся всех трех сторон треугольника, называется вписанной окружностью треугольника. |
| Описанная окружность | Окружность, проходящая через все три вершины треугольника, называется описанной окружностью треугольника. |
Это лишь некоторые из связей, которые треугольник имеет с другими фигурами. Треугольник является фундаментальной формой геометрии и его связи с другими фигурами позволяют нам лучше понять и анализировать геометрическую природу различных фигур.
Формулы и теоремы о треугольниках
В геометрии и математике существует множество формул и теорем, связанных с треугольниками. Некоторые из них являются основными и широко используются при решении задач и вычислениях.
- Формулы для вычисления площади треугольника:
- Площадь треугольника можно вычислить, зная длины двух сторон и угла между ними, по формуле: S = (1/2) * a * b * sin(C), где a и b - длины сторон, С - угол между ними.
- Для вычисления площади треугольника, если известны длины всех трех сторон, можно использовать формулу Герона: S = √(p * (p - a) * (p - b) * (p - c)), где p - полупериметр треугольника, равный (a + b + c)/2.
- Основные теоремы о треугольниках:
- Теорема Пифагора: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов: c² = a² + b², где c - гипотенуза, a и b - катеты треугольника.
- Теорема синусов: В любом треугольнике отношение каждой стороны к синусу противолежащего ей угла равно величине радиуса описанной окружности: a / sin(A) = b / sin(B) = c / sin(C).
- Теорема косинусов: В любом треугольнике квадрат длины одной стороны равен сумме квадратов длин двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: a² = b² + c² - 2 * b * c * cos(A).
- Теорема о медиане: Медиана треугольника делит ее в отношении 2:1. То есть, сумма квадратов длин двух меньших по длине отрезков медианы равна удвоенному квадрату длины большей медианы: 2 * (a² + b²) = 4 * c², где c - длина большей медианы, a и b - длины двух меньших медианы.
Это лишь некоторые формулы и теоремы, связанные с треугольниками. Знание этих формул и теорем позволяет решать разнообразные задачи и проводить вычисления в геометрии и математике. Изучение свойств треугольников имеет большое значение при решении задач разной сложности в различных областях науки и техники.








