Характеристическое уравнение является одним из ключевых понятий в теории управления и математической физике. Это уравнение позволяет определить свойства линейной динамической системы, такие как ее устойчивость, колебательность и амплитудно-частотные характеристики.
Характеристическое уравнение является полиномом n-ой степени, где n - порядок системы, то есть количество ее уравнений. Корни этого уравнения, так называемые характеристические значения, определяются исходя из физических свойств системы и ее параметров.
Основная роль характеристического уравнения заключается в определении степени устойчивости системы. Если все корни характеристического уравнения имеют отрицательные вещественные части, то система считается асимптотически устойчивой, то есть ее выход с течением времени сходится к некоторому установившемуся значению.
Кроме того, характеристическое уравнение позволяет найти собственные режимы колебаний системы, которые определяют ее частотные свойства. Зная характеристические значения, можно определить естественные частоты колебаний системы и даже форму колебаний.
Таким образом, характеристическое уравнение играет важную роль в анализе и проектировании динамических систем, позволяя определить их устойчивость и колебательность. Знание свойств характеристического уравнения позволяет разрабатывать эффективные методы управления системами и повышать их эффективность и надежность.
Определение характеристического уравнения
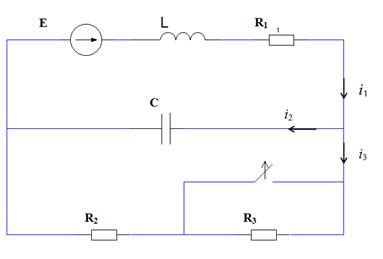
Для линейной системы с постоянными коэффициентами, представленной дифференциальным уравнением, характеристическое уравнение определяет ее устойчивость и специфические свойства.
Характеристическое уравнение формулируется как уравнение степени n, где n - порядок дифференциального уравнения, характеризующего систему.
Для линейной системы с постоянными коэффициентами в форме уравнения:
any(n)(t) + an-1y(n-1)(t) + ... + a1y'(t) + a0y(t) = 0
Характеристическое уравнение записывается как:
ansn + an-1sn-1 + ... + a1s + a0 = 0
Где s - переменная, представляющая собой комплексное число показателя экспоненты для системы в представлении Лапласа.
Решение характеристического уравнения позволяет определить корни уравнения, которые называются характеристическими значениями или собственными значениями системы. Эти значения влияют на стабильность и динамику системы.
Основные свойства системы, такие как устойчивость, неустойчивость, колебательность, амплитуда колебаний, зависят от значений собственных значений, определенных характеристическим уравнением.
Характеристическое уравнение позволяет провести анализ и изучить динамическое поведение системы без явного решения дифференциального уравнения.
Таким образом, характеристическое уравнение играет важную роль в анализе систем и определении их свойств, что позволяет инженерам и ученым разрабатывать и улучшать различные технические системы.
Значение характеристического уравнения в системах
Характеристическое уравнение получается путем приравнивания нулю определителя матрицы коэффициентов характеристического полинома. Это полином n-ой степени, где n - порядок системы. Решением этого уравнения являются корни полинома, называемые собственными значениями системы.
Знание собственных значений позволяет определить такие важные характеристики системы, как устойчивость, колебательность и амплитуда колебаний. Собственные значения отражают особенности динамики системы и могут быть как действительными, так и комплексными числами.
Если все собственные значения системы имеют отрицательные вещественные части, то система будет устойчивой. Если хотя бы одно собственное значение имеет положительную вещественную часть, то система будет неустойчивой.
Собственные значения, являющиеся чисто мнимыми или комплексными числами с нулевой вещественной частью, указывают на наличие колебательности в системе. Размеры и амплитуды колебаний определяются значениями мнимой части комплексных собственных значений.
Таким образом, характеристическое уравнение позволяет получить информацию о стабильности и поведении системы. Оно служит основой для анализа и оптимизации работы различных технических и физических систем, а также применяется в контролирующих алгоритмах, математическом моделировании и других областях науки и техники.
Связь характеристического уравнения с передаточной функцией

Одно из ключевых свойств системы, определяемых характеристическим уравнением, - ее устойчивость. Устойчивая система будет иметь ограниченный отклик на любое начальное возмущение, в то время как неустойчивая система будет расходиться. Характеристическое уравнение позволяет определить значения параметров системы, при которых она будет устойчивой.
Также характеристическое уравнение связано с передаточной функцией системы. Передаточная функция является отношением Лапласа выходного сигнала к входному сигналу и может быть выражена через характеристическое уравнение. Для линейных стационарных систем передаточная функция имеет вид:
$$H(s) = \\frac{N(s)}{D(s)}$$
где $$N(s)$$ и $$D(s)$$ - многочлены, соответствующие числителю и знаменателю характеристического уравнения, соответственно.
Передаточная функция позволяет анализировать отклик системы на входной сигнал и определять ее частотные и временные характеристики. Также она может использоваться для проектирования и синтеза системы, позволяя задавать желаемые свойства и требования.
Таким образом, характеристическое уравнение и передаточная функция являются основными инструментами в анализе и проектировании динамических систем. Понимание их связи позволяет более точно определить свойства и поведение системы.
Факторы, влияющие на свойства характеристического уравнения
Характеристическое уравнение имеет ключевое значение при анализе свойств системы. Его решение определяет, какие значения могут принимать собственные числа матрицы, связанной с системой, и тем самым определяет динамические свойства системы.
Существует несколько факторов, которые влияют на свойства характеристического уравнения:
- Размерность матрицы системы: Характеристическое уравнение зависит от размерности матрицы системы. Чем больше размерность матрицы, тем сложнее анализировать его свойства и решать уравнение.
- Вид матрицы системы: Форма и значения элементов матрицы также влияют на свойства характеристического уравнения. Например, если матрица является симметричной, уравнение будет иметь особые свойства.
- Условия задачи: Решение характеристического уравнения может быть чувствительно к определенным условиям задачи. Например, изменение граничных условий может привести к изменению собственных значений и, следовательно, к изменению динамических свойств системы.
- Значения собственных чисел: Собственные числа, полученные при решении характеристического уравнения, определяют динамические свойства системы. Например, положительные собственные числа указывают на неустойчивое поведение системы, а отрицательные - на устойчивое поведение.
Все эти факторы влияют на свойства характеристического уравнения и, соответственно, на свойства системы в целом. Понимание и анализ этих факторов позволяет предсказывать и управлять поведением системы и использовать характеристическое уравнение в различных областях, таких как управление, электротехника, механика и другие.
Анализ корней характеристического уравнения
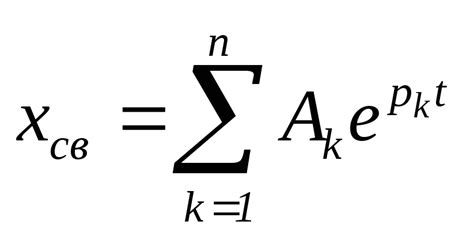
Пусть дано характеристическое уравнение вида:
p(s) = ansn + an-1sn-1 + ... + a1s + a0 = 0
где an, an-1, ..., a0 - коэффициенты уравнения, а s - неизвестная переменная.
Анализ корней уравнения проводится путем нахождения всех его корней. Корни могут быть комплексными или вещественными числами, и их количество равно степени уравнения. Найденные корни уравнения позволяют определить свойства системы.
Если все корни уравнения имеют отрицательные вещественные части, то система является асимптотически устойчивой. Это означает, что при отсутствии внешних воздействий система будет стремиться к состоянию равновесия.
Если хотя бы один из корней имеет положительную вещественную часть, то система является неустойчивой. Это означает, что при отсутствии внешних воздействий система будет стремиться к неограниченному росту или колебаниям.
Если некоторые корни имеют нулевую вещественную часть, то система может быть либо предельно устойчивой, либо границей устойчивости, что зависит от других свойств системы.
Процесс анализа корней характеристического уравнения позволяет инженерам и ученым определить правильность выбора параметров системы, предсказать ее поведение и внести корректировки для достижения требуемых результатов.
Влияние коэффициентов на форму характеристического уравнения
Коэффициенты характеристического уравнения - это числовые значения, которыми умножаются соответствующие степени оператора передаточной функции системы. Изменение этих коэффициентов может повлиять на форму уравнения и, следовательно, на свойства системы.
Один из самых важных параметров, влияющих на форму характеристического уравнения, - это коэффициенты знаменателя передаточной функции системы. Они определяют корни характеристического уравнения - значения, при которых уравнение обращается в ноль. Корни могут быть действительными или комплексными числами.
Действительные корни характеристического уравнения указывают на наличие нулей или полюсов в передаточной функции системы. Они могут свидетельствовать о наличии режимов колебаний или затухающего сигнала в системе. Комплексные корни определяют наличие колебательного режима в системе, который может проявляться в виде синусоидальных колебаний.
Коэффициенты числителя передаточной функции также влияют на форму характеристического уравнения. Они определяют числитель уравнения, который влияет на амплитуду передаточной функции и связанные с этим свойства системы.
Изменение коэффициентов передаточной функции может изменить форму характеристического уравнения и, следовательно, свойства системы. Например, изменение коэффициентов может повлиять на устойчивость системы, наличие колебаний или затухание сигнала. Поэтому анализ и определение значений коэффициентов является важной задачей при проектировании и анализе систем управления.
Примеры применения характеристического уравнения в реальных системах

Автоматическое регулирование процессов
Характеристическое уравнение играет важную роль в автоматическом регулировании процессов. Например, при настройке ПИД-регуляторов используется анализ и определение корней характеристического уравнения системы. Это позволяет оптимизировать регулирование, улучшить переходные процессы и подавить колебания.
Электроника и электрические цепи
Характеристическое уравнение применяется в анализе и проектировании электрических цепей. Например, для нахождения собственных частот колебательных контуров или определения устойчивости электрических систем. Знание корней характеристического уравнения позволяет предсказать поведение электрической системы в различных режимах работы.
Механические системы
Характеристическое уравнение используется для анализа и моделирования механических систем. Например, при изучении колебаний маятников или рассмотрении динамики движения тел. Корни характеристического уравнения позволяют определить собственные частоты и формы колебаний системы.
Системы управления
Характеристическое уравнение находит широкое применение в проектировании и анализе систем управления. Например, при исследовании устойчивости и определении свойств различных регуляторов. Анализ корней характеристического уравнения позволяет определить устойчивость системы управления и предсказать ее поведение при различных входных воздействиях.
Все эти примеры демонстрируют важность характеристического уравнения в анализе и проектировании различных систем. Нахождение корней уравнения позволяет определить основные свойства системы и предсказать ее поведение в различных условиях.
Выводы
Характеристическое уравнение имеет решения, называемые характеристическими корнями, которые представлены в виде комплексных чисел. Реальная и мнимая части характеристических корней могут определить тип колебаний системы: затухающие, колебательные или экспоненциально растущие.
Анализ характеристического уравнения позволяет также определить значение присоединенных функций, таких как переходная и импульсная функции, которые описывают поведение системы во времени и частотной области.
Таким образом, понимание и решение характеристического уравнения является важным инструментом для анализа и проектирования динамических систем, таких как электрические цепи, механические системы, системы управления и другие.








