В математике существует особое понятие - взаимная перпендикулярность сторон треугольника. Это значит, что две стороны треугольника ортогональны друг другу, то есть образуют прямой угол. Исследование взаимной перпендикулярности может иметь важное значение при решении геометрических задач и доказательстве теорем.
Для того чтобы две стороны треугольника были перпендикулярными друг другу, они должны встречаться в одной из вершин треугольника под прямым углом. Если стороны AB и BC треугольника ABC перпендикулярны друг другу, то это обозначается как AB⊥BC.
Взаимная перпендикулярность сторон треугольника может быть использована для доказательства различных свойств треугольника. Многие теоремы основываются на этом понятии. Например, теорема о высотах треугольника утверждает, что высоты, проведенные к сторонам треугольника, перпендикулярны этим сторонам.
Пример: Рассмотрим треугольник ABC. Предположим, что AC⊥BC. Тогда мы можем сделать вывод, что сторона AB является гипотенузой прямоугольного треугольника ACB.
Взаимная перпендикулярность сторон треугольника является важным понятием в геометрии и может помочь в изучении его свойств и особенностей. Это понятие используется в различных теоремах и задачах для решения геометрических проблем.
Взаимно перпендикулярные стороны треугольника: объяснение и примеры
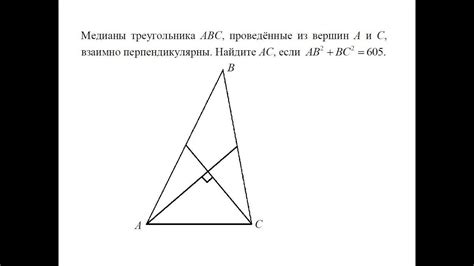
В треугольнике есть три стороны, и некоторые из них могут быть взаимно перпендикулярными. Чтобы понять, что означает взаимное перпендикулярность сторон треугольника, нужно разобраться в определении перпендикулярности.
Перпендикулярные линии или отрезки на плоскости пересекаются друг под прямым углом, то есть углы между ними равны 90 градусам. В треугольнике взаимно перпендикулярные стороны – это две стороны, которые пересекаются под прямым углом.
Примером треугольника с двумя взаимно перпендикулярными сторонами может служить прямоугольный треугольник. В таком треугольнике одна из его сторон является основанием, а другая – высотой. Они перпендикулярны друг другу, образуя прямой угол.
Взаимно перпендикулярные стороны треугольника могут быть полезными для вычисления его площади и для решения некоторых геометрических задач. Кроме того, такие стороны позволяют определить тип треугольника: если две стороны перпендикулярны и третья не перпендикулярна им, то треугольник является прямоугольным.
Взаимно перпендикулярные стороны треугольника играют важную роль при решении геометрических задач и могут помочь лучше понять геометрию треугольников в целом.
Значение перпендикулярных сторон треугольника
Перпендикулярные стороны треугольника могут иметь разную длину и определять отношения между сторонами и углами треугольника. Они также могут служить основой для построения и измерения других сторон и углов треугольника.
Примеры перпендикулярных сторон треугольника:
- Основание и высота: В прямоугольном треугольнике одна сторона является основанием, а другая сторона - высотой. Они перпендикулярны друг другу и образуют прямой угол.
- Биссектриса и медиана: В некоторых случаях биссектриса и медиана треугольника могут быть перпендикулярными друг к другу.
- Боковая сторона и основание прямоугольного треугольника: В прямоугольном треугольнике одна из сторон является боковой стороной, а другая сторона - основанием. Они перпендикулярны друг другу.
Знание и использование перпендикулярных сторон треугольника позволяет более просто и точнее решать различные задачи, связанные с изучением и анализом треугольников.
Объяснение взаимной перпендикулярности
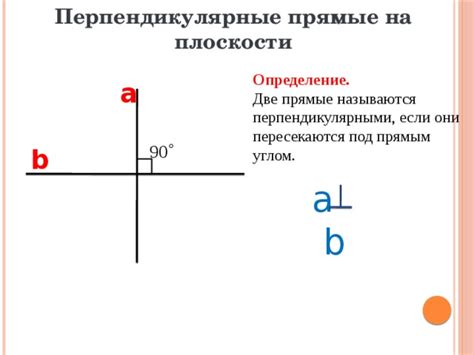
Взаимная перпендикулярность в треугольнике означает, что две стороны треугольника перпендикулярны друг другу. Это означает, что угол между этими сторонами равен 90 градусов.
Взаимная перпендикулярность играет важную роль в геометрии. Она позволяет определить множество свойств и отношений в треугольнике.
Примером такого треугольника может служить прямоугольный треугольник. В прямоугольном треугольнике две стороны, образующие прямой угол, являются взаимно перпендикулярными.
Стороны треугольника:
|
В данном примере, сторона A и сторона B являются взаимно перпендикулярными, так как угол между ними равен 90 градусов.
Взаимная перпендикулярность может быть использована для решения различных задач в геометрии, например, для нахождения длин сторон треугольника или для определения его типа.
Примеры перпендикулярных сторон
Взаимно перпендикулярные стороны треугольника образуют прямой угол в точке их пересечения. Рассмотрим несколько примеров треугольников с перпендикулярными сторонами:
| Пример | Описание |
|---|---|
 | В этом примере треугольник ABC имеет две перпендикулярные стороны: AB и BC. Они пересекаются в точке B, образуя прямой угол. |
 | В данном примере треугольник DEF также имеет две перпендикулярные стороны: DE и DF. Они пересекаются в точке D, образуя прямой угол. |
 | В этом примере треугольник XYZ имеет две перпендикулярные стороны: XY и YZ. Они пересекаются в точке Y, образуя прямой угол. |
Таким образом, в треугольнике взаимно перпендикулярные стороны могут быть расположены различными способами, но всегда образуют прямой угол в точке их пересечения.









