Гипербола - это одна из фигур, которая изучается в математике. Она выглядит как две ветви, которые расходятся, но приближаются к определенной прямой линии, называемой асимптотой. Уравнение асимптот гиперболы дает нам возможность определить положение и форму этих асимптот.
Уравнение асимптот гиперболы состоит из двух частей - первая часть определяет расстояние между асимптотами, а вторая - угол наклона асимптот относительно осей координат. Зная эти параметры, мы можем точно предсказать форму и положение гиперболы.
Уравнение асимптот гиперболы имеет важное практическое применение в различных областях, включая физику, инженерию и экономику. Например, в физике оно может использоваться для моделирования движения частиц в электрическом поле, в инженерии - для проектирования оптических систем, а в экономике - для анализа спроса и предложения.
Уравнение асимптот гиперболы: понятие и особенности
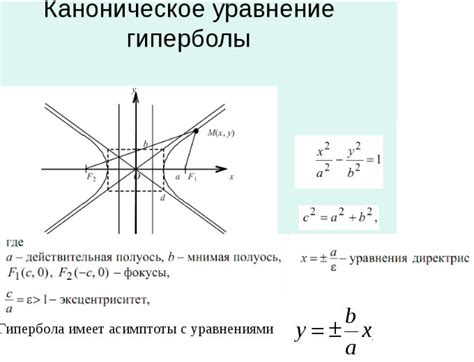
Уравнение асимптот гиперболы представляет собой систему двух уравнений, определяющую положение асимптот относительно гиперболы. Обычно данная система выглядит следующим образом:
- Уравнение первой асимптоты: y = kx + b1
- Уравнение второй асимптоты: y = kx + b2
Здесь k - наклон асимптоты, b1 и b2 - свободные коэффициенты.
Особенностью уравнения асимптот гиперболы является то, что значения наклона и свободных коэффициентов могут быть определены на основе параметров гиперболы. Например, в случае гиперболы с центром в начале координат (0,0), наклон асимптот будет равен отношению коэффициентов a и b в уравнении гиперболы: k = a/b.
Уравнение асимптот гиперболы играет важную роль в анализе свойств и поведении данной геометрической фигуры. С помощью уравнения асимптот можно определить направление и угол наклона асимптот, а также выяснить, будет ли гипербола ограничена и где она имеет вершины.
Данные особенности уравнения асимптот гиперболы позволяют упростить анализ гиперболических функций, находить точки пересечения гиперболы с асимптотами и решать задачи, связанные с построением и использованием гипербол в различных областях науки и техники.
Описание понятия гиперболы
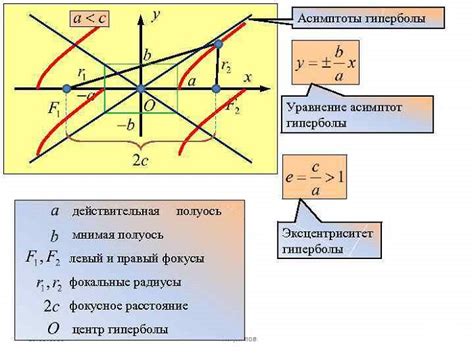
Гипербола обладает следующими характеристиками:
- У неё есть два фокуса и два податливых направления;
- Она не имеет центра симметрии;
- У неё есть асимптоты, которые являются прямыми, к которым стремятся ветви гиперболы;
- У неё есть оси симметрии, которые проходят через фокусы и пересекаются в центре (если он существует);
- У неё есть вершина, которая является точкой, где ветви гиперболы располагаются ближе всего друг к другу.
Гипербола имеет много различных применений в науке и технике. Например, она может использоваться для моделирования электрических и магнитных полей, оптических систем, антенн и телекоммуникационных систем. Также гипербола часто применяется в математических исследованиях и в анализе данных.
Принципы построения уравнения гиперболы

1. Выбор центра гиперболы: для построения уравнения гиперболы необходимо выбрать центр гиперболы. Центр гиперболы является точкой пересечения осей симметрии гиперболы.
2. Определение фокусов гиперболы: после выбора центра гиперболы, определяются фокусы гиперболы, которые являются точками на главной оси гиперболы.
3. Определение полуосей гиперболы: полуоси гиперболы – это расстояния от центра гиперболы до вершин гиперболы. Они определяются величиной параметра гиперболы.
4. Выбор направления гиперболы: в зависимости от возможных направлений гиперболы выбирается положительное или отрицательное значение параметра гиперболы.
5. Составление уравнения гиперболы: уравнение гиперболы может быть записано в общем виде, учитывая параметры гиперболы, полуоси и координаты центра гиперболы.
Принципы построения уравнения гиперболы дают возможность определить форму и расположение гиперболы на плоскости и использовать уравнение гиперболы для решения задач геометрии и аналитической геометрии.
Важность асимптот гиперболы
Асимптоты гиперболы можно использовать для определения основных свойств этой кривой. Например, зная угловой коэффициент одной из асимптот и расстояние от центра до асимптоты, можно найти уравнение гиперболы или расстояние между фокусами.
Также асимптоты гиперболы позволяют понять различные важные характеристики этой кривой, такие как её симметричность, ориентация и направление. Знание этих свойств помогает решать задачи, связанные с определением положения точек на графике гиперболы или определением границ области, ограниченной этой кривой.
Таким образом, понимание и использование асимптот гиперболы является необходимым при изучении и анализе данной кривой, а также при решении задач, связанных с ней. Они помогают нам более глубоко понять устройство и свойства гиперболы, а также применить их в практических задачах.
Правила использования уравнения асимптот гиперболы
- Для нахождения уравнения асимптот необходимо знать уравнение гиперболы. Уравнение асимптот может быть найдено путем устранения члена с наибольшей степенью из уравнения гиперболы.
- Уравнение асимптот имеет вид y = mx + c, где m - наклон асимптоты, а c - значение смещения.
- Наклон асимптоты определяется коэффициентами при x и y в уравнении гиперболы. Если уравнение гиперболы имеет вид Ax^2 - By^2 = C, то наклон асимптоты будет равен ±B/A.
- Значение смещения можно найти, зная координаты центра гиперболы. Если центр гиперболы имеет координаты (h, k), то значение смещения будет равно k - mh.
- Уравнение асимптот является приближением для гиперболы в бесконечности. Гипербола будет приближаться к асимптотам по мере ее удаления от центра.
Правила использования уравнения асимптот гиперболы помогут найти параметры асимптот и лучше понять геометрию гиперболы. Это важные инструменты при решении задач из различных областей математики и физики.








