Неравенства – одно из основных понятий математики, которое является инструментом для сравнения чисел и выражений. Они состоят из знака сравнения и двух выражений, объединенных этим знаком.
Целочисленные решения неравенств — это значения переменных, которые удовлетворяют неравенству, и являются целыми числами. Нахождение их количества и значений может быть полезным при решении математических задач, определении области допустимых значений или нахождении интервала, в котором может находиться искомое значение.
Существует несколько методов и подходов к определению количества целочисленных решений неравенства и их значения. Один из таких методов – графический способ, который позволяет наглядно представить неравенства на координатной плоскости и определить область, в которой можно найти решение. Но этот метод не всегда удобен и эффективен, особенно когда мы имеем дело с большим количеством переменных или сложными выражениями.
Для решения неравенств с целыми числами обычно используют алгебраический метод. Он заключается в поиске решений путем анализа и преобразования выражений, применяя различные алгебраические операции.
В этой статье мы рассмотрим несколько примеров и методов определения количества целочисленных решений неравенств и их значения. Вы узнаете о ключевых понятиях, таких как интервалы, области допустимых значений, алгебраические преобразования и другие аспекты, которые помогут вам эффективно находить решения для различных видов неравенств.
Методы подсчета количества целочисленных решений неравенства

Для подсчета количества целочисленных решений неравенства существует несколько методов:
Метод перебора
Данный метод заключается в последовательном переборе всех возможных значений переменной и проверке каждого значения на удовлетворение неравенству. Если значение удовлетворяет неравенству, оно считается целочисленным решением. Этот метод прост в применении, но может быть очень трудоемким при большом диапазоне значений переменной, поэтому часто применяется для поиска малых значений.
Метод замены переменных
Данный метод заключается в замене переменной в неравенстве таким образом, чтобы оно стало удобным для подсчета количества целочисленных решений. Например, если уравнение содержит дроби или корни, переменные могут быть заменены на новые переменные, не содержащие таких сложностей. После этого можно использовать метод перебора или другие методы для подсчета количества решений.
Метод математического анализа
Этот метод основан на применении математического анализа для определения количества целочисленных решений. Для этого используются математические функции, такие как полиномы, экспоненциальные функции и логарифмы. Применение этого метода требует хорошего знания математического анализа и может быть достаточно сложным.
Выбор метода зависит от конкретной задачи и ее условий. В разных ситуациях может потребоваться использование комбинации нескольких методов или различных приближенных подходов для получения точного или приближенного количества целочисленных решений неравенства.
Подсчет через перебор
Для начала, необходимо определить границы для каждой переменной в неравенстве. Затем, можно приступить к перебору значений переменных начиная с минимального значения и увеличивая их до максимального значения. При каждой итерации проверяется, является ли текущее значение переменных решением неравенства.
Если текущее значение переменных удовлетворяет условию неравенства, то считается одно допустимое решение. Это решение также может иметь свои уникальные значения переменных, которые можно сохранить для дальнейшего анализа или использования.
Однако, следует учесть, что при большом количестве переменных и широком диапазоне их значений, перебор может быть затратным и непрактичным. В таких случаях, необходимо применять более эффективные методы подсчета и анализа целочисленных решений неравенств.
Использование математических неравенств
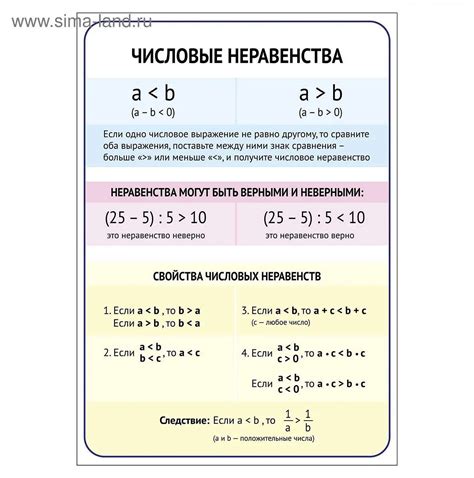
Для нахождения количества целочисленных решений неравенства необходимо выполнить ряд шагов:
- Будем искать все целые числа, которые могут быть решениями неравенства.
- Подставим найденные значения в неравенство и проверим их.
- Занесем все найденные целочисленные решения в список.
После выполнения этих шагов, мы получим список всех целочисленных решений неравенства и сможем установить их значения.
Например, рассмотрим неравенство 2x + 3 < 9. Чтобы найти количество целочисленных решений и их значение, выполним следующие шаги:
- Переберем все возможные значения для переменной x: -4, -3, -2, -1, 0, 1, 2, 3, 4 и т.д.
- Подставим каждое значение x в неравенство и проверим его. Например, при x = -4 получаем 2(-4) + 3 < 9. Решим это уравнение: -8 + 3 < 9. Получаем -5 < 9, что является истиной.
- Занесем каждое найденное значение x в список целочисленных решений: -4.
Повторив эти шаги для всех возможных значений переменной x, мы сможем найти все целочисленные решения неравенства и определить их значения.
Таким образом, использование математических неравенств позволяет нам находить количество целочисленных решений неравенства и устанавливать их значения.
Применение графического метода
Графический метод активно применяется для решения неравенств и нахождения их количества целочисленных решений. Основная идея метода заключается в построении графика функции, соответствующей неравенству, и анализе ее поведения на интервалах.
Для построения графика неравенства необходимо:
- Выразить неравенство в виде функции, содержащей переменные.
- Построить график данной функции.
- Проанализировать поведение графика на интервалах и определить значения переменных, при которых неравенство выполняется.
После построения графика неравенства можно определить количество целочисленных решений неравенства и их значение. Для этого необходимо проанализировать пересечения графика с осью абсцисс и точки, в которых график пересекает целочисленные значения.
| Неравенство | График | Количество решений | Значение решений |
|---|---|---|---|
| x > 0 |  | Бесконечно много | x > 0 |
| x ≤ 5 |  | 6 | x = 0, x = 1, x = 2, x = 3, x = 4, x = 5 |
Таким образом, применение графического метода позволяет наглядно представить неравенство и его решения, а также удобно проводить анализ и находить количество и значение целочисленных решений.








