В геометрии каждому углу соответствует определенное число, и эти числа являются пропорциональными углам. Это означает, что при изменении размера угла его числовое значение также изменяется. Пропорциональность углов позволяет нам легче работать с ними и решать различные задачи в геометрии.
Пропорциональность углов проявляется в том, что при увеличении или уменьшении угла в определенное количество раз, его числовое значение также увеличивается или уменьшается в том же самом количестве раз. Например, если мы увеличиваем угол в два раза, его числовое значение также удваивается.
Знание пропорциональности углов помогает решать задачи связанные с подобными фигурами. Например, если мы знаем, что два треугольника подобны, то пропорции углов этих треугольников будут равны. Это позволяет нам вычислять недостающие углы в подобных фигурах и решать различные задачи в геометрии.
Пропорциональность углов играет важную роль в решении задач геометрии и помогает нам лучше понять принципы построения и измерения различных фигур. Знание этого понятия позволяет нам более эффективно решать задачи и применять геометрию в реальной жизни.
Углы и числа: безграничные возможности геометрии

Пропорциональность углов и чисел означает, что в соответствующих фигурах два угла могут быть пропорциональны двум числам. Это означает, что если один угол в фигуре увеличивается или уменьшается в несколько раз, второй угол тоже увеличивается или уменьшается в такое же количество раз. Это свойство углов позволяет нам использовать математическую алгебру для решения геометрических задач.
Когда мы говорим о пропорциональности углов и чисел, мы можем использовать такие понятия, как сходство треугольников и параллельные линии. Например, если два треугольника подобны, то все их углы пропорциональны. Это значит, что если один угол в первом треугольнике увеличивается в 2 раза, то соответствующий угол во втором треугольнике тоже увеличивается в 2 раза.
Также, когда имеются параллельные линии, их пересекают две прямые линии, называемые трансверсалями. Трансверсальные линии создают соответствующие углы (лежат по разные стороны трансверсали и пересекаются с параллельными линиями). Если две параллельные линии пересекаются трансверсалью, то соответствующие углы пропорциональны. Это свойство позволяет нам вычислять углы, используя информацию о параллельных и перпендикулярных линиях.
Пропорциональность углов и чисел имеет широкое применение в анализе и решении различных геометрических задач. Например, она позволяет нам вычислять неизвестные углы, определять сходство фигур, проводить геометрические преобразования и многое другое. Понимание этой концепции позволяет нам расширить наши знания о геометрии и использовать ее для решения сложных задач.
Таким образом, пропорциональность углов и чисел открывает для нас безграничные возможности в области геометрии. Это позволяет нам анализировать и решать сложные задачи, используя математические методы и инструменты. Геометрия является фундаментальной областью науки, и понимание пропорциональности углов и чисел позволяет нам расширить наши возможности в этой области.
Углы: отражение мира в величинах
В геометрии угол представляет собой область пространства между двумя лучами, исходящими из одной точки. Угол измеряется отношением его величины к величине прямого угла, который равен 90 градусам. Углы могут быть измерены в градусах, радианах или градах.
Пропорциональность угла относительно числа означает, что можно связать величину угла с числом. Например, если угол равен 45 градусов, его можно записать как отношение к прямому углу в виде 45/90 или 1/2. Таким образом, пропорциональные углы могут быть выражены в виде дробей или десятичных чисел.
Применение пропорциональности углов в геометрии позволяет нам решать различные задачи. Например, зная значение одного угла, мы можем найти значение другого угла в треугольнике или находить соответствующие углы при построении фигур и пространственных объектов.
Более того, понимание свойств пропорциональности углов позволяет нам делать выводы о формах и пропорциях предметов в реальном мире. Угол наклона крыши дома, угол наклона линий в перспективных рисунках или угол наклона страницы книги - все эти примеры демонстрируют пропорциональность углов и их значение в создании и анализе геометрических объектов.
Числа и их взаимосвязь с углами
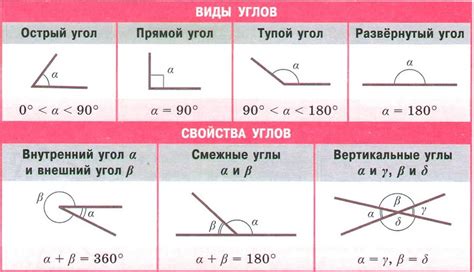
В геометрии углы могут быть пропорциональны числам. Это значит, что значения углов могут быть выражены исходя из определенных числовых соотношений.
Одним из основных примеров пропорциональности чисел и углов является соотношение между градусами и полным оборотом. Полный оборот в геометрии равен 360 градусов. Таким образом, можно сказать, что 360 градусов пропорциональны полному обороту.
Кроме того, в тригонометрии также применяется пропорциональность чисел и углов. Например, в прямоугольном треугольнике длины сторон могут быть выражены с помощью тригонометрических функций: синуса, косинуса и тангенса. Эти функции определены для любого угла и имеют пропорциональные значения.
Пропорциональность чисел и углов играет важную роль в геометрии и тригонометрии, позволяя определять и вычислять значения углов с использованием математических соотношений. Это позволяет более точно анализировать и изучать геометрические фигуры и применять их в различных областях науки и техники.
Пропорциональность: ключевая концепция геометрии
Пропорциональность углов и чисел означает, что величина углов соотносится с числами таким образом, что их отношение остается неизменным. Например, если мы имеем два острых угла, то их меры также будут пропорциональны.
Применение пропорциональности в геометрии позволяет нам решать различные задачи, связанные с нахождением меры углов. Например, если нам известна мера одного угла и мы хотим найти меру другого угла, мы можем использовать пропорциональность для определения этого значения.
Пропорциональность углов и чисел также играет важную роль в доказательствах геометрических теорем. Она позволяет нам установить связь между различными углами и доказать их равенство или соотношение.
В заключение, пропорциональность углов и чисел является важным понятием в геометрии, которое позволяет нам определить меру углов и решать задачи, связанные с их поиском. Эта концепция также помогает нам в доказательствах теорем и установлении соотношений между углами.
Углы пропорциональны: что это значит?

Для того чтобы понять, как применить эту концепцию в геометрии, необходимо знать, что углы могут быть измерены в градусах или радианах. Градусы представляют собой наиболее распространенную систему измерения углов, которая делит один оборот восемьюдесятью равными частями. Радианы, с другой стороны, представляют собой альтернативную систему измерения углов, в которой один оборот соответствует $2\pi$ радиан.
Применяя концепцию пропорциональности к углам, можно сравнить два или несколько углов и сказать, что они имеют одинаковое отношение, даже если их величины разные. Например, два угла могут иметь соотношение 1:2, что означает, что второй угол в два раза больше первого. Такое отношение можно записать в виде уравнения $\frac{\alpha}{\beta} = \frac{1}{2}$, где $\alpha$ и $\beta$ - это два угла. Это отношение может быть выражено как отношение двух длинных сторон, двух радиусов или двух дуг, которые соответствуют этим углам.
Знание понятия пропорциональности углов позволяет решать различные геометрические задачи, такие как нахождение неизвестных углов, вычисление отношений между углами и определение свойств треугольников и многоугольников. Оно также используется в изучении тригонометрии и других математических дисциплин, связанных с геометрией.








