Треугольник, круг и квадрат являются основными геометрическими фигурами, которые мы встречаем повсюду – от природных образований до архитектурных сооружений. Каждая из этих фигур имеет свою уникальность и символическое значение, которое отражает особенности и значимость для нашей культуры и понимания окружающего мира. В данной статье мы рассмотрим все три фигуры и проанализируем их значения и ассоциации, которые они вызывают у нас.
Треугольник – одна из простейших геометрических фигур, обладающая тремя сторонами и тремя углами. Он символизирует стабильность, активность и движение вперед. Часто треугольник ассоциируется с пирамидами и горами, что дает ему крепкость и силу. Эта фигура используется в различных культурных и религиозных символах, таких как Древо Жизни или Треугольник Пожертвования. В магии треугольник считается символом трансформации и прозрения, ведь он содержит в себе три направления – прошлое, настоящее и будущее.
Круг – самая простая и совершенная фигура в геометрии. Без начала и конца, он олицетворяет бесконечность, гармонию и совершенство. Круг также связывается с символами солнца, луны, земли и вселенной. Он представляет целостность и полноту, а его гладкие кривые формы приносят чувство спокойствия и единства. В различных культурах круг употреблялся как символ божественности, духовности и бессмертия.
Квадрат – прямоугольник с одинаковыми сторонами, олицетворяет равновесие, порядок и стабильность. Эта фигура проста и прямолинейна, что выражает чувство надежности и непреложности. Квадрат часто ассоциируется с элементами земли, такими как полы, стены и фундаменты. Он используется в архитектуре и градостроительстве как средство создания симметричных и устойчивых конструкций. В символике квадрат может выражать различные понятия, такие как гармония, справедливость, равенство или ограничение.
Треугольник: геометрическая фигура с тремя сторонами
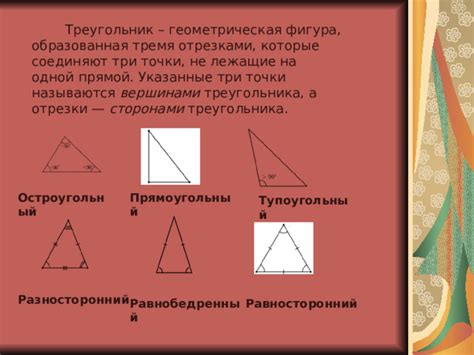
Основные характеристики треугольника - это его стороны и углы. Сумма углов треугольника всегда равна 180 градусам. Треугольники могут быть разных типов в зависимости от своих сторон и углов.
По сторонам треугольники могут быть равносторонними, равнобедренными или разносторонними. Равносторонний треугольник имеет три равные стороны и три равных угла. Равнобедренный треугольник имеет две равные стороны и два равных угла. Разносторонний треугольник имеет все три стороны разной длины и все три угла разных величин.
По углам треугольники могут быть остроугольными, прямоугольными или тупоугольными. Остроугольный треугольник имеет три угла меньше 90 градусов. Прямоугольный треугольник имеет один прямой угол, равный 90 градусам. Тупоугольный треугольник имеет один тупой угол, больше 90 градусов.
Треугольники имеют разнообразные свойства и используются в различных областях науки и техники. Изучение треугольников является одной из основ геометрии и дает основу для решения множества задач и проблем в различных областях знания.
Основные характеристики треугольника
Основные характеристики треугольника:
1. Стороны: Треугольник имеет три стороны, которые могут быть различной длины. Стороны могут быть равными или разными.
2. Углы: Треугольник имеет три угла, каждый из которых обозначается как A, B и C. Сумма углов треугольника всегда равна 180 градусам.
Пример: Угол A + Угол B + Угол C = 180 градусов.
3. Типы треугольников: В зависимости от длины и углов треугольник может быть классифицирован как равносторонний, равнобедренный, разносторонний или остроугольный, тупоугольный или прямоугольный треугольник.
4. Площадь: Площадь треугольника можно найти, зная длины его сторон или высоту и основание треугольника. Формула для расчета площади может быть разной в зависимости от известных данных.
5. Периметр: Периметр треугольника - это сумма длин его сторон. Формула для расчета периметра треугольника проста: Периметр = Длина стороны A + Длина стороны B + Длина стороны C.
Разновидности треугольников: равносторонний, равнобедренный и разносторонний
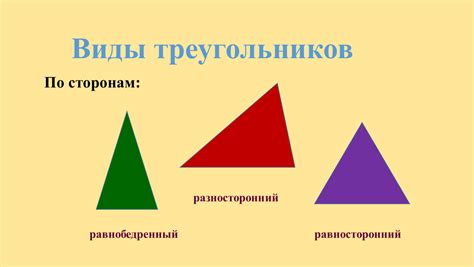
- Равносторонний треугольник – это треугольник, у которого все три стороны равны друг другу. Углы в равностороннем треугольнике также равны и составляют по 60 градусов. Пример равностороннего треугольника: треугольник со сторонами 5 см, 5 см, 5 см.
- Равнобедренный треугольник – это треугольник, у которого две стороны равны друг другу. Углы в равнобедренном треугольнике могут быть разными, но два угла при основании всегда равны между собой. Пример равнобедренного треугольника: треугольник со сторонами 4 см, 4 см, 6 см.
- Разносторонний треугольник – это треугольник, у которого все три стороны разные. Углы в разностороннем треугольнике могут быть разными и не зависят от длин сторон. Пример разностороннего треугольника: треугольник со сторонами 3 см, 4 см, 5 см.
Треугольники являются одними из основных геометрических фигур и находят широкое применение в различных областях знаний, включая математику, физику, архитектуру и искусство. Знание разновидностей треугольников и их свойств помогает в решении геометрических задач и анализе фигур.
Круг: геометрическая фигура с равными удалениями от центра
Основной характеристикой круга является радиус, который определяется как расстояние от центра круга до любой его точки. Радиус является постоянным величиной и одновременно является расстоянием от центра круга до его границ.
Круг обладает множеством свойств и характеристик, которые делают его уникальной геометрической фигурой:
- Круг обладает бесконечным количеством оси симметрии. То есть, любая прямая, проходящая через центр круга, является осью симметрии, разделяющей его на две равные части.
- Периметр круга называется окружностью. Длина окружности вычисляется по формуле: Длина окружности = 2πr, где r - радиус круга, а π - математическая постоянная, примерно равная 3.14159.
- Площадь круга вычисляется по формуле: Площадь круга = πr2, где r - радиус круга, а π - математическая постоянная, примерно равная 3.14159.
- Формула для нахождения площади сегмента круга (части круга между хордой и дугой) имеет вид: Площадь сегмента = (θ/360°)πr2 - (1/2)r2sinθ, где r - радиус круга, а θ - центральный угол (в градусах).
Круг является универсальной геометрической фигурой и широко используется в науке, инженерии, архитектуре и других областях. С его помощью можно создавать круглые формы, моделировать круглые объекты, расчитывать площади и объемы, а также решать множество задач и задачек в геометрии и математике.
Основные характеристики круга
Круг имеет следующие основные характеристики:
• Радиус - это расстояние от центра круга до любой точки на его границе. Обозначается символом "r".
• Диаметр - это отрезок, соединяющий две точки на границе круга и проходящий через его центр. Диаметр равен удвоенному значению радиуса и обозначается символом "d".
• Окружность - это граница круга, состоящая из всех точек, находящихся на одинаковом расстоянии от его центра. Окружность имеет длину, называемую периметром или длиной окружности. Периметр окружности можно рассчитать с помощью формулы: P = 2πr, где "P" - периметр, "π" - число пи (приблизительно равно 3,14159) и "r" - радиус.
• Площадь - это мера поверхности круга, ограниченной его границей. Площадь круга можно рассчитать с помощью формулы: S = πr², где "S" - площадь и "r" - радиус.
Круг является одной из основных геометрических фигур и широко используется в различных областях, таких как математика, физика, инженерия и геодезия.
Формула площади круга и его окружности
Окружность является замкнутой кривой и имеет ряд характеристик, таких как радиус, диаметр, длина окружности и площадь.
Площадь круга определяется формулой:
S = π * r2
где S - площадь круга, π - число пи (приближенное значение 3.14159), r - радиус круга.
Таким образом, чтобы найти площадь круга, необходимо умножить квадрат радиуса круга на значение числа пи.
Квадрат: геометрическая фигура с четырьмя равными сторонами

Квадрат является одним из фундаментальных элементов в геометрии и наиболее распространенной фигурой в повседневной жизни. Он широко используется в архитектуре, дизайне интерьера, на картах, в математике и в других областях.
Отличительной особенностью квадрата является его регулярная форма: все стороны и углы квадрата равны между собой. В результате, квадрат обладает свойствами, которые делают его удобным для различных вычислений и конструкций.
Площадь квадрата вычисляется как произведение длины одной из его сторон на эту же длину: S = a * a, где S - площадь квадрата, а - длина стороны.
Периметр квадрата определяется как сумма всех его сторон: P = 4a, где P - периметр квадрата, а - длина стороны.
Квадрат также является идеальной формой для равномерного распределения площадей. Например, простые участки земли или городские кварталы часто имеют форму квадрата для оптимального использования пространства.








