Равноудаленная точка от вершин треугольника является такой точкой, которая расположена на одинаковом расстоянии от каждой из вершин. Это интересное и важное свойство, которое находит применение в различных областях математики, физики и дизайна.
Одно из основных свойств равноудаленной точки заключается в том, что она всегда находится внутри треугольника. Если рассмотреть треугольник как геометрическую фигуру, то равноудаленная точка будет являться ее центром масс. Это означает, что она делит каждую сторону треугольника пополам, а также является точкой пересечения медиан, выходящих из вершин треугольника.
Равноудаленная точка имеет также ряд интересных свойств, связанных с углами треугольника. Например, если провести линии, соединяющие равноудаленную точку с вершинами треугольника, то эти линии будут образовывать равные углы с каждой из вершин. Более того, сумма углов, образованных равноудаленной точкой и вершинами треугольника, всегда будет составлять 180 градусов.
Изучение свойств равноудаленной точки от вершин треугольника помогает лучше понять его геометрическую структуру и особенности. Также это знание может быть полезно в практических приложениях, например, при решении задач по конструированию и дизайну.
Свойства равноудаленной точки
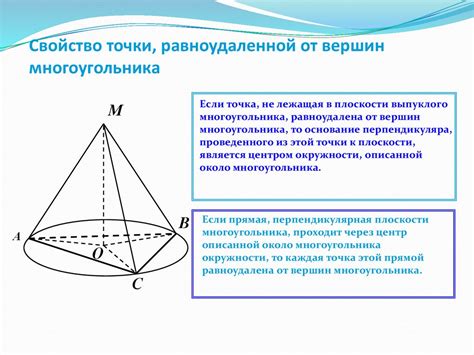
Основные свойства равноудаленной точки:
- Равноудаленная точка лежит на биссектрисе угла треугольника.
- Во всех треугольниках равноудаленная точка совпадает с центром окружности, описанной около треугольника.
- Точка пересечения медиан треугольника является равноудаленной точкой.
- Если провести от равноудаленной точки перпендикуляры к сторонам треугольника, то они будут равны.
Свойства равноудаленной точки широко применяются в геометрии и могут быть использованы для решения различных задач, например, при определении центра масс треугольника или при построении окружности, описанной около треугольника.
Определение равноудаленной точки
Другими словами, равноудаленная точка от вершин треугольника равноудалена от всех трех вершин.
Равноудаленная точка от вершин треугольника также называется центром описанной окружности треугольника, поскольку данная точка является центром окружности, которая проходит через все вершины треугольника.
Для нахождения равноудаленной точки можно использовать различные методы, включая геометрические и алгебраические подходы.
Знание равноудаленной точки от вершин треугольника имеет большое значение в геометрии и находит применение при решении различных задач, связанных с треугольниками и окружностями.
Свойства равноудаленной точки

Свойства равноудаленной точки:
- Равноудаленная точка всегда находится внутри треугольника.
- Равноудаленная точка от вершин треугольника является центром окружности, описанной вокруг треугольника.
- Величина расстояния от равноудаленной точки до каждой из вершин треугольника одинакова.
- Центр окружности, описанной вокруг треугольника, является равноудаленной точкой от его вершин.
Свойства равноудаленной точки от вершин треугольника важны в геометрии и находят применение при решении различных задач и построений.
Применение равноудаленной точки
Одним из применений равноудаленной точки является определение центра окружности, описанной вокруг треугольника. Эта точка является равноудаленной точкой от трех вершин треугольника и называется центром описанной окружности. Она используется в геометрических вычислениях и конструировании объектов.
Еще одним применением равноудаленной точки является определение центра тяжести треугольника. Центр тяжести – это точка, в которой сумма масс трех вершин треугольника равна их общей массе, а момент импульса равен нулю. Центр тяжести является равноудаленной точкой от трех вершин и является важным понятием в физике и механике.
Также равноудаленная точка находит применение в алгоритмах и программировании. Она может быть использована для определения точки, которая находится на равном расстоянии от нескольких объектов или векторов. Это позволяет решать задачи симметрии, поиска местонахождения и другие задачи в компьютерной графике и вычислительной геометрии.
| Применение | Область |
|---|---|
| Определение центра описанной окружности треугольника | Геометрия |
| Определение центра тяжести треугольника | Физика, механика |
| Определение точки на равном расстоянии от нескольких объектов | Алгоритмы, программирование |








