Когда мы говорим о принадлежности точки углу, мы имеем в виду, что данная точка лежит на одной из сторон или в вершине угла. Это понятие весьма важно в геометрии и математике, так как позволяет определить, как точка связана с фигурой или объектом.
Определение принадлежности точки углу может быть полезным при решении задач на планиметрии, строительстве, геодезии и других областях, связанных с измерением и построением объектов. Зная координаты точки и угла, мы можем определить ее положение относительно угла.
Существует несколько способов определить, принадлежит ли точка углу. Можно использовать геометрический подход, основанный на сравнении углов и длин сторон, или алгебраический подход, основанный на координатах точки и угла. В обоих случаях нужно учитывать особенности конкретной задачи и иметь навыки работы с геометрическими и алгебраическими методами решения.
Важно понимать, что принадлежность точки углу может быть относительной и зависит от выбранной системы координат или параметров угла. Поэтому при работе с такими задачами необходимо быть внимательным и внимательно анализировать условия задачи.
Точка и ее принадлежность углу

Для определения принадлежности точки углу используются различные методы. Один из них - это сравнение координат точки с координатами вершин угла. Если координаты точки находятся между координатами вершин угла, то она принадлежит углу.
Также, с помощью угловой меры можно определить, принадлежит ли точка углу. Если угол образованный точкой и вершинами угла равен или меньше 180 градусов, то точка принадлежит углу. Если же угол больше 180 градусов, то точка не принадлежит углу.
Знание того, принадлежит ли точка углу, помогает в решении геометрических задач и построении фигур. Оно также может быть полезным при работе с координатами в пространстве.
Определение угла и точки
Точка - это элементарная геометрическая фигура, не имеющая ни длины, ни ширины, ни высоты. Она является одним из основных понятий в геометрии и математике в целом. Точка обозначается символом и может быть определена по координатам на плоскости или в пространстве.
Определить, принадлежит ли точка углу, можно с помощью геометрических построений и аналитических методов. Для этого необходимо знать координаты вершины угла и координаты точки. Если точка находится на продолжении одного из лучей угла или внутри его, то говорят, что она принадлежит углу. Если же точка находится вне угла или на продолжении другого луча, то она не принадлежит углу.
Понятие принадлежности
Чтобы определить принадлежит ли точка углу, мы должны знать его границы и координаты данной точки. Для простых углов, таких как прямой, острый или тупой, определение принадлежности может быть достаточно простым. Например, если точка находится внутри угла, то мы можем сказать, что она ему принадлежит.
Однако, существуют также сложные углы, у которых более сложные границы и форма. Для определения принадлежности точки такому углу может потребоваться более тщательный анализ и использование геометрических методов.
Например, для определения принадлежности точки треугольнику можно использовать такой метод:
- Найдите все стороны треугольника и определите их уравнения.
- Составьте систему уравнений, которая будет описывать все стороны треугольника.
- Решите эту систему уравнений и найдите точку пересечения сторон треугольника.
- Если найденная точка пересечения совпадает с исследуемой точкой, то можно сказать, что точка принадлежит треугольнику.
Важно понимать, что принадлежность точки фигуре может меняться в зависимости от ее положения относительно границ фигуры. Кроме того, принадлежность точки может быть определена не только для углов, но и для других фигур, таких как окружности, параллелограммы и т.д.
Таким образом, понятие принадлежности является важным при решении геометрических задач и играет важную роль в анализе фигур и их свойств.
Важность определения
Определение принадлежности точки углу имеет важное значение в геометрии и математике. Это позволяет нам понять не только, принадлежит ли точка конкретному углу, но и использовать эту информацию для решения различных задач.
Знание, что точка принадлежит углу, может быть полезно при нахождении смежных углов, проведении линий, построении геометрических фигур и решении задач на координатной плоскости. Кроме того, это может помочь нам определить, находится ли точка внутри или снаружи угла, что может быть полезно для изучения свойств углов и их взаимного расположения.
Для точного определения принадлежности точки углу, мы используем различные методы и правила геометрии. Часто углы определяются своими вершинами и сторонами. Если точка лежит на одной из сторон угла или совпадает с его вершиной, она считается принадлежащей углу.
Правильное определение принадлежности точки углу позволяет нам проводить точные вычисления и рассчитывать координаты точек на плоскости. Это необходимое предпосылка для решения различных задач и исследования геометрических объектов.
Доказательство принадлежности точки углу
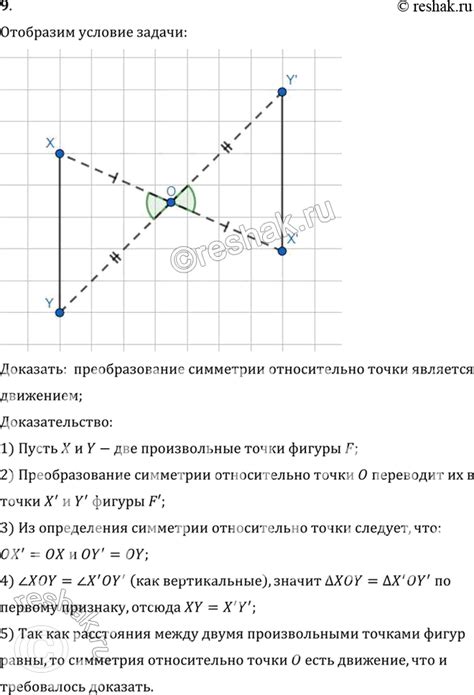
Для доказательства принадлежности точки углу необходимо проверить, лежит ли она на одной из сторон или на вершине данного угла.
Если точка лежит на одной из сторон, то координаты этой точки должны удовлетворять уравнению этой стороны. Например, для угла АВС и точки М, лежащей на стороне АВ, координаты точки М должны удовлетворять уравнению линии АВ.
Если точка лежит на вершине угла, то координаты этой точки должны совпадать с координатами вершины угла. Например, для угла АВС и точки В, координаты точки В должны совпадать с координатами вершины В.
Таким образом, чтобы доказать принадлежность точки углу, необходимо провести проверку на лежание точки на стороне или на вершине угла, исходя из координат точки и угла.
Положение точки внутри угла
Когда мы говорим о положении точки внутри угла, мы имеем в виду то, находится ли точка внутри самого угла или же на его границе. Если точка лежит внутри угла, то она находится внутри его углового конуса, в противном случае, точка находится на одной из сторон граничного ребра угла.
Для определения положения точки внутри угла, можно использовать различные методы. Один из таких методов - это определение расстояния от точки до каждой из двух сторон угла. Если расстояние до каждой стороны меньше или равно нулю, то точка лежит внутри угла. Если же хотя бы одно из расстояний положительно, то точка находится на одной из сторон угла или вне его.
Еще один способ определить положение точки внутри угла - это проверить, лежит ли точка внутри углового конуса угла. Для этого можно провести лучи, начинающиеся в вершине угла и проходящие через каждую из сторон. Если точка лежит по одну сторону от всех лучей, то она находится внутри углового конуса и, следовательно, внутри угла. Если точка лежит по разные стороны от одного или нескольких лучей, то она находится на границе угла или вне его.
Положение точки на сторонах угла
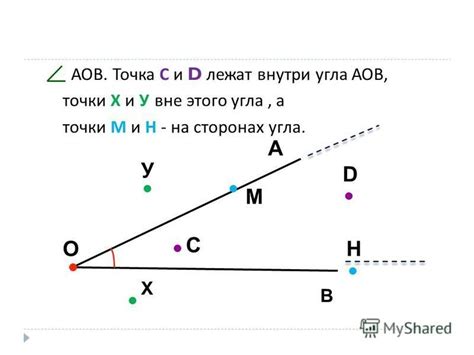
Угол образуется двумя лучами, называемыми сторонами угла, и одной общей точкой, называемой вершиной угла. Иногда возникает необходимость определить, находится ли какая-либо точка на одной из сторон угла. Для этого можно использовать следующий метод:
1. Рассмотрим стороны угла, на которых находится точка. Обозначим их значимыми буквами.
| Сторона угла | Обозначение |
| Луч 1 | AB |
| Луч 2 | AC |
2. Зададим точку, которую необходимо проверить, обозначением D.
3. Проверим, лежит ли точка D на стороне угла AB или AC.
Для этого проведем две прямые, соединяющие точки D и A с вершиной угла C:
- Если точка D находится по одну сторону от прямой AD и по другую сторону от прямой AC, то точка D лежит на стороне угла AB.
- Если точка D находится по одну сторону от прямой AD и по другую сторону от прямой AB, то точка D лежит на стороне угла AC.
- Если точка D не удовлетворяет ни одному из этих условий, то она не лежит на сторонах угла.
Таким образом, определение положения точки на сторонах угла позволяет удобно ориентироваться при решении геометрических задач и проведении различных построений.
Геометрические соотношения
Точка, принадлежащая углу, обладает определенными геометрическими свойствами:
- Точка лежит и на одной из сторон угла, и на его вершине;
- Расстояние от точки до вершины угла равно расстоянию от этой точки до каждой из сторон угла;
- Сумма углов, образуемых линиями, проходящими через точку и каждую из сторон угла, равна 180 градусам (если угол прямой) или 360 градусам (если угол полный).
Определить, принадлежит ли точка заданному углу, можно анализируя координаты точки и координаты вершин угла. Если координаты точки соответствуют условиям вышеупомянутых свойств, то можно сказать, что точка принадлежит углу.
Практическое применение

Понимание того, что точка принадлежит углу, имеет важное практическое значение в различных областях, включая математику, физику, геометрию и программирование. Ниже приведены некоторые примеры применения этого концепта.
- Геодезия: точка принадлежит углу важна при измерении углов между различными точками на земной поверхности. Например, при определении направления движения по компасу.
- Архитектура: точка принадлежит углу используется для расчета углов, необходимых для построения зданий и других строений. Это помогает создавать прочные и устойчивые конструкции.
- Компьютерная графика: определение того, принадлежит ли точка углу, позволяет программистам создавать реалистичные трехмерные модели и 3D-анимацию.
- Механика: различные приложения в механике, такие как расчет сил и векторов, требуют определения, принадлежит ли точка углу.
Это лишь некоторые примеры использования концепции принадлежности точки углу. В реальности они широко применяются во многих областях науки и технологий, где точное определение позиции точки в отношении угла является важной задачей.
Интересные факты
- Определение принадлежности точки углу является важным концептом в геометрии.
- Для определения, принадлежит ли точка углу, необходимо знать координаты вершин угла и координаты точки.
- Если точка лежит на одной из сторон угла, она также считается принадлежащей углу.
- Если точка находится внутри угла, то она принадлежит этому углу.
- Если точка лежит вне угла, то она не принадлежит углу.
- Использование формулы длины вектора или теоремы косинусов помогает определить принадлежность точки углу.
- Если все вершины угла и точка лежат на одной прямой, то угол называется прямым углом.
- На плоскости существуют углы, у которых сумма мер углов равна 180 градусов.
- Греческая буква "альфа" часто используется для обозначения угла.








