Сумма натуральных чисел - это результат сложения всех натуральных чисел от 1 до заданного числа. Эта математическая операция является простой, но важной, и широко используется в различных областях науки и повседневной жизни. Понимание суммы натуральных чисел позволяет не только решать различные задачи, но и развивать абстрактное мышление.
Как определить сумму натуральных чисел?
Для определения суммы натуральных чисел от 1 до n можно использовать формулу: S = (n * (n + 1)) / 2, где S - сумма, а n - число, до которого нужно сложить натуральные числа. Эта формула была впервые доказана математиком Карлом Фридрихом Гауссом и является одним из классических результатов в арифметике.
Например, чтобы найти сумму всех натуральных чисел от 1 до 10, можно воспользоваться формулой: S = (10 * (10 + 1)) / 2 = 55. Таким образом, сумма всех натуральных чисел от 1 до 10 равна 55.
Знание суммы натуральных чисел может быть полезно при решении различных задач, таких как вычисление средних значений, нахождение суммы элементов последовательностей и рядов, а также при решении задач комбинаторики и вероятности. Более того, понимание принципов сложения натуральных чисел помогает в развитии логического мышления и способствует пониманию более сложных математических концепций и операций.
Определение суммы натуральных чисел

Формула для вычисления суммы натуральных чисел:
- Sn = 1 + 2 + 3 + ... + n
Натуральные числа - это положительные целые числа, начиная с 1 и не имеющие дробной или отрицательной части.
Примеры вычисления суммы натуральных чисел:
- Для n = 4:
- S4 = 1 + 2 + 3 + 4 = 10
- S6 = 1 + 2 + 3 + 4 + 5 + 6 = 21
- S10 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55
Сумма натуральных чисел является важным понятием в математике и имеет широкий спектр применений, включая решение задач комбинаторики, алгебры и анализа. Понимание определения суммы натуральных чисел позволяет лучше разбираться в этих областях и упрощает решение математических задач.
Что такое сумма натуральных чисел?
Сумму натуральных чисел можно представить в виде арифметической прогрессии, где каждое следующее число получается путём добавления к предыдущему числу единицы. Например, сумма всех натуральных чисел до 5 будет равна 1 + 2 + 3 + 4 + 5 = 15.
Для нахождения суммы натуральных чисел существуют формулы, позволяющие упростить вычисления. Наиболее часто используемая формула - это сумма арифметической прогрессии:
| Формула | Пример |
|---|---|
| S = (n * (n + 1)) / 2 | Сумма чисел от 1 до 10: (10 * (10 + 1)) / 2 = 55 |
Также сумму натуральных чисел можно вычислить с помощью цикла или рекурсии. Но использование формулы - более эффективный и быстрый способ.
Сумма натуральных чисел широко применяется в математике и науке. Она помогает решать задачи связанные с подсчётом и вычислениями. Например, сумма натуральных чисел может использоваться для определения среднего значения или для нахождения общей суммы элементов в последовательности чисел.
Как вычислить сумму натуральных чисел?
Сумма натуральных чисел может быть вычислена с помощью формулы суммы арифметической прогрессии. Для этого необходимо знать первый и последний члены прогрессии, а также количество членов.
Формула для вычисления суммы арифметической прогрессии имеет вид:
S = (a + b) * n / 2
Где:
- S - сумма
- a - первый член прогрессии
- b - последний член прогрессии
- n - количество членов прогрессии
Например, чтобы вычислить сумму натуральных чисел от 1 до 10, необходимо подставить значения в формулу:
S = (1 + 10) * 10 / 2 = 55
Таким образом, сумма натуральных чисел от 1 до 10 равна 55.
Примеры вычисления суммы натуральных чисел
Пример 1:
Вычислить сумму всех натуральных чисел от 1 до 10.
Для решения этой задачи можно воспользоваться формулой арифметической прогрессии:
S = (a + b) * n / 2
Где:
S – сумма
a – первое число
b – последнее число
n – количество чисел в последовательности
Подставляя значения в формулу, получим:
S = (1 + 10) * 10 / 2 = 55
Ответ: сумма всех натуральных чисел от 1 до 10 равна 55.
Пример 2:
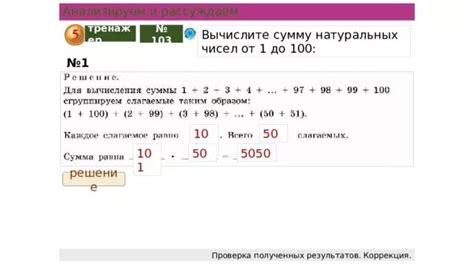
Вычислить сумму всех натуральных чисел от 1 до 100.
Аналогично предыдущему примеру, используем формулу арифметической прогрессии:
S = (a + b) * n / 2
S = (1 + 100) * 100 / 2 = 5050
Ответ: сумма всех натуральных чисел от 1 до 100 равна 5050.
Пример 3:
Вычислить сумму всех чётных натуральных чисел от 2 до 20.
Для решения данной задачи нужно выделить из последовательности только чётные числа и просуммировать их. Для этого можно воспользоваться формулой арифметической прогрессии, но с учётом шага:
S = (a + b) * n / 2
Где:
S – сумма
a – первое чётное число
b – последнее чётное число
n – количество чётных чисел в последовательности
Подставляя значения в формулу, получим:
S = (2 + 20) * 10 / 2 = 110
Ответ: сумма всех чётных натуральных чисел от 2 до 20 равна 110.
Особенности суммы натуральных чисел

Значение суммы натуральных чисел может быть найти по формуле: S = (n * (n + 1)) / 2, где S - сумма, n - количество чисел.
Одна из особенностей суммы натуральных чисел заключается в том, что результат сложения зависит от значения числа n. Чем больше значение n, тем больше будет сумма натуральных чисел. Например, сумма натуральных чисел от 1 до 10 равна 55, а сумма натуральных чисел от 1 до 100 уже равна 5050.
Еще одна особенность суммы натуральных чисел состоит в том, что при сложении чисел от одного до n, каждое число встречается два раза. Например, при сложении чисел от 1 до 5, число 1 встречается в начале и в конце суммы, число 2 встречается вторым и предпоследним, и так далее. Поэтому можно заметить, что сумма натуральных чисел равна половине произведения количества чисел на их среднее арифметическое.








