Что означает система несовместна метода Гаусса

Метод Гаусса – это один из основных методов решения систем линейных уравнений. Он был разработан немецким математиком Карлом Фридрихом Гауссом в конце XVIII века и до сих пор широко применяется в математике, физике, экономике и других областях.

Система линейных уравнений является несовместной в том случае, если не существует ни одного решения, то есть значения переменных, которые удовлетворяют всем уравнениям системы. Это означает, что уравнения противоречивы или некоторые из них являются неверными.

При использовании метода Гаусса для решения системы линейных уравнений сначала приводят систему к треугольному виду, т.е. упорядочивают уравнения таким образом, чтобы в начале стояли уравнения, в которых присутствуют все переменные, затем уравнения с меньшим количеством переменных и, наконец, уравнения, в которых присутствуют только свободные члены.

Если при приведении системы к треугольному виду в одном из этапов получается невозможная система, то это означает, что исходная система несовместна.

Несовместность системы линейных уравнений может иметь практический смысл во множестве различных задач. Например, в экономике это может означать отсутствие равновесия в рыночной модели или невозможность удовлетворения всех ограничений. В физике это может означать несогласованность между измеряемыми величинами и теоретическими моделями.

Система уравнений и метод Гаусса

Одним из методов решения систем уравнений является метод Гаусса. Он основан на элементарных преобразованиях строк матрицы системы и позволяет свести исходную систему к эквивалентной системе, которая уже имеет простой и наглядный вид.

Метод Гаусса заключается в следующих шагах:

Составление расширенной матрицы системы, где каждое уравнение представляется в виде строки, а коэффициенты и свободные члены записываются в столбцы.
Приведение матрицы к треугольному виду с помощью элементарных преобразований строк, таких как умножение строки на число, прибавление строки к другой строке и перестановка строк местами.
Обратный ход метода Гаусса, в результате которого получаем матрицу диагонального вида, где все элементы над главной диагональю равны нулю.
Нахождение решений системы путем обратного хода метода Гаусса: подстановка полученных значений переменных в исходное уравнение и проверка его выполнимости.

Если после применения метода Гаусса система имеет хотя бы одно уравнение с противоречивыми условиями или одно из уравнений является линейной комбинацией других уравнений, то говорят, что система несовместна. В этом случае не существует решений системы уравнений.

Метод Гаусса является одним из основных инструментов линейной алгебры и применяется для решения систем уравнений в различных областях науки и техники.

Определение системы несовместна

Система линейных алгебраических уравнений называется несовместной, если ее решение не существует, то есть не существует таких значений переменных, которые удовлетворяли бы все уравнения системы. В таком случае система несовместна и решение не может быть найдено.

Это может произойти по нескольким причинам:

Система содержит противоречивые уравнения, которые невозможно выполнить одновременно. Например, одно уравнение говорит о том, что переменная должна быть равна 2, а другое уравнение говорит о том, что переменная должна быть равна 3.
Система содержит недостаточное количество уравнений, чтобы определить значения всех переменных. В этом случае, есть несколько возможных вариантов значений переменных, и только дополнительная информация может помочь определить их точные значения.

Определение системы несовместна важно, так как позволяет определить, что система уравнений не имеет решения и требуется использование других методов или подходов для решения задачи.

Рассмотрение метода Гаусса

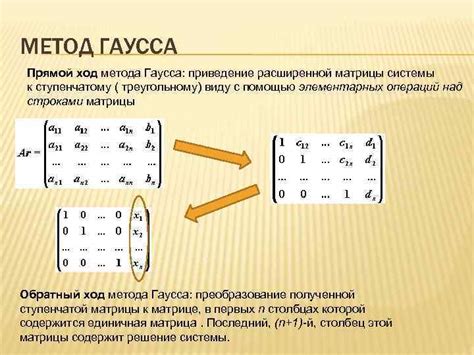
Основная идея метода Гаусса заключается в построении треугольной матрицы путем применения элементарных преобразований к исходной матрице уравнений. Элементарные преобразования включают в себя умножение строк на число, сложение строк, перестановку строк.

После приведения матрицы к треугольному виду, можно легко найти решение системы уравнений. Для этого производятся обратные элементарные преобразования, в результате которых получается одно решение или бесконечное количество решений.

Однако, иногда после применения метода Гаусса к системе уравнений получается противоречие, и система не имеет решений. Это означает, что исходная система уравнений несовместна. Несовместность системы выражается в том, что появляется строка матрицы, в которой все элементы равны нулю, и соответствующий элемент столбца свободных членов не равен нулю.

Таким образом, система несовместна метода Гаусса, если после применения элементарных преобразований к матрице уравнений образуется противоречие, то есть, появляется строка, в которой все элементы равны нулю, и соответствующий элемент столбца свободных членов не равен нулю.

Признаки несовместности системы уравнений

Система линейных уравнений называется несовместной, если не существует такого набора значений переменных, при котором все уравнения системы выполняются одновременно. То есть, такая система не имеет решений.

Существует несколько признаков, по которым можно определить несовместность системы уравнений:

Если в системе есть хотя бы одно противоречивое уравнение, то система является несовместной. Противоречивые уравнения противоречат друг другу и невозможно найти значения переменных, при которых оба уравнения выполняются.
Если в системе есть хотя бы одно неверное уравнение, то система также является несовместной. Неверные уравнения не могут быть выполнены ни при каких значениях переменных.
Если в системе есть уравнение, которое приводит к противоречию с другим уравнением при любых значениях переменных, то система также является несовместной. Примером может служить система уравнений, в которой одно из уравнений содержит выражение "x + y = 5", а другое уравнение содержит выражение "x + y = 7".
Если в системе есть бесконечно много решений, то она также считается несовместной. Несмотря на то, что у такой системы есть решения, их бесконечность делает систему несовместной.

Знание этих признаков позволяет быстро определить, является ли данная система уравнений совместной или несовместной. Это важно для решения задачи и применения соответствующих математических методов.

Примеры систем уравнений и метода Гаусса

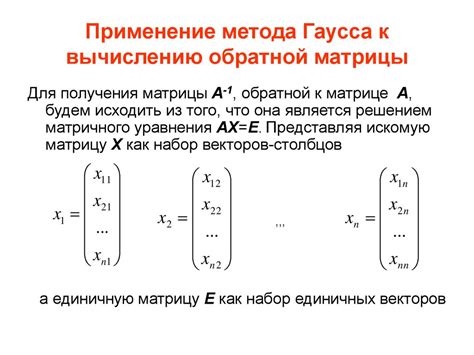
Рассмотрим несколько примеров систем уравнений и применение метода Гаусса для их решения.

Пример 1:

Рассмотрим систему линейных уравнений:

2x + 3y - z = 1
4x + 2y + 2z = 6
3x - y + z = 3

В этом примере система уравнений является совместной, так как имеет решение.

Применим метод Гаусса для её решения:

Приводим систему к треугольному виду:

2x + 3y - z = 1
0x - 4y + 4z = 4
0x + 0y + 2z = 2

Находим решение системы:

x = 1
y = 1
z = 1

Пример 2: