Производная функции является одной из основных концепций математического анализа и науки о данных. Этот показатель позволяет определить, как изменяется значение функции при изменении аргумента. Производная играет важную роль во множестве областей, включая физику, экономику, биологию и машинное обучение.
Основными понятиями, связанными с производной, являются скорость изменения и наклон касательной. Производная в точке представляет собой предел отношения изменения значения функции к изменению аргумента при стремлении изменения аргумента к нулю. Этот предел показывает, насколько быстро изменяется функция в каждой конкретной точке.
Производная функции определяет наклон касательной линии к графику функции в данной точке. Касательная линия является наилучшим линейным приближением функции в окрестности этой точки. Наклон касательной линии равен производной функции в этой точке. Это позволяет определить, как функция ведет себя вблизи каждой точки и выяснить ее поведение в целом на всем протяжении.
Зачем нужна производная в математике?

Производная позволяет нам определить скорость изменения или наклон кривой функции в каждой ее точке. С помощью производной можно выявить точки экстремума, а также дать ответы на вопросы о максимальных и минимальных значениях функций.
Производная позволяет решать оптимизационные задачи, находить оптимальные значения переменных и эффективно решать задачи в экономике, физике, инженерии, биологии и других науках. Она также является неотъемлемой частью в математическом моделировании и численных методах.
Кроме того, производная позволяет определить гладкость функций, т.е. она позволяет нам понять, насколько функция "плавная" и как часто меняется ее наклон.
В итоге, знание и понимание производной позволяет нам обнаруживать и анализировать особенности функций, а также находить решения сложных задач, которые требуют определения изменения величин и функций в зависимости от различных факторов.
Какие понятия лежат в основе производной?
- Тангенс угла наклона: производная функции в точке определяет тангенс угла наклона касательной к графику функции в этой точке.
- Предел: производная является пределом отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю.
- Касательная: производная функции в точке также определяет уравнение касательной, проходящей через эту точку.
- Информация о скорости и ускорении: производная функции по времени часто интерпретируется как скорость изменения функции или ускорение объекта, описываемого этой функцией.
Понимание этих понятий позволяет лучше оценивать изменения функций и их поведение и становится основой для более сложных концепций и расширенных приложений производной.
Основные принципы вычисления производных
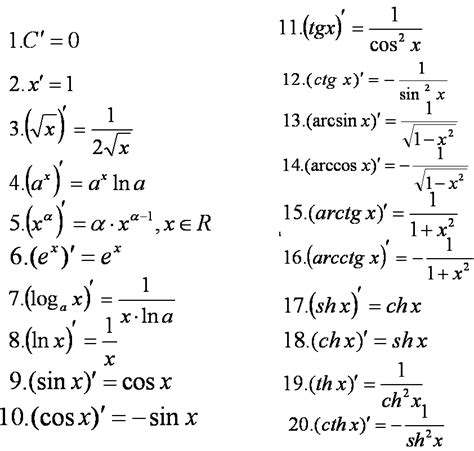
1. Принцип малых приращений. Производная функции в точке равна пределу отношения приращения функции к приращению ее аргумента при стремлении последнего к нулю.
2. Принцип линейности. Производная суммы (или разности) функций равна сумме (или разности) их производных. Производная произведения функции на константу равна произведению этой константы на производную функции. Производная произведения (или частного) функций равна определенному выражению, называемому правилом дифференцирования сложной функции.
3. Принцип дифференцирования сложной функции. Если переменная зависит от другой переменной, которая, в свою очередь, зависит от третьей переменной, то производную от первой переменной можно найти, применив правило дифференцирования сложной функции.
4. Принцип дифференцирования обратной функции. Если функция F(x) строго возрастает (убывает) на некотором интервале и имеет обратную функцию G(y), то если производная G'(y) не обращается в ноль, то производная F'(x) равна обратной производной G'(y).
5. Принцип дифференцирования неявной функции. Если уравнение связывает переменные x и y, причем y можно выразить явно через x, то производную y по переменной x можно найти, используя правило дифференцирования неявной функции.
6. Принцип дифференцирования параметрически заданной функции. Производную y по переменной x можно найти, используя правило дифференцирования параметрически заданной функции.
7. Принцип дифференцирования логарифма и экспоненты. Производная логарифма функции равна производной функции, деленной на значение самой функции. Производная экспоненты функции равна произведению производной функции на значение самой функции.
Эти основные принципы вычисления производных широко применяются в математике, физике, экономике, и других науках для анализа и оптимизации функций и процессов.
Какие свойства имеет производная?
- Линейность: производная линейной комбинации двух функций равна линейной комбинации их производных. То есть, если две функции имеют производные, то их комбинация также имеет производную.
- Правило суммы: производная суммы двух функций равна сумме их производных. То есть, если две функции имеют производные, то производная их суммы равна сумме их производных.
- Правило произведения: производная произведения двух функций равна произведению производной первой функции и второй функции плюс произведение первой функции и производной второй функции. То есть, если две функции имеют производные, то производная их произведения равна этому выражению.
- Правило частного: производная частного двух функций равна разности произведения производной первой функции и второй функции и произведения первой функции и производной второй функции, деленной на квадрат второй функции. То есть, если две функции имеют производные, то производная их частного равна этому выражению.
- Правило цепной дроби: производная сложной функции равна произведению производной внешней функции и производной внутренней функции. То есть, если функция представлена в виде композиции двух функций, то производная этой функции равна произведению производных этих функций.
Знание и применение этих свойств позволяет упростить вычисления производных и решать сложные задачи, связанные с изучением изменения функций.
Примеры применения производной в реальной жизни

1. Физика: Производная позволяет моделировать и анализировать изменение скорости и ускорения тела. Например, при решении задач о движении автомобиля на основе данных о его скорости, производная помогает найти изменение скорости и ускорения в зависимости от времени. Он также используется в физических законах Ньютона для описания динамики движения.
2. Экономика: Производная применяется для анализа спроса и предложения на товары и услуги. Она позволяет определить точку, где спрос и предложение встречаются и достигается равновесие на рынке. Кроме того, производная используется для моделирования и анализа функций издержек и доходов компании с целью максимизации прибыли.
3. Информатика: Производная применяется в алгоритмах машинного обучения и оптимизации. Например, в алгоритмах градиентного спуска производная используется для нахождения оптимальной комбинации параметров модели, которая минимизирует ошибку. Она также используется для анализа и оптимизации производительности программ и алгоритмов.
4. Медицина: Производная применяется для анализа и моделирования процессов в организме, таких как рост опухолей, регулирование инсулина в организме диабетиков и контроль давления крови. Она помогает в определении оптимального времени и дозировки для лечения и предотвращения болезней.
Приведенные примеры лишь небольшая часть сфер, в которых производная играет важную роль. Она является мощным математическим инструментом, который помогает понимать и анализировать изменения и зависимости в различных областях науки и жизни.








