Предел функции – это одно из фундаментальных понятий математического анализа, которое используется для изучения поведения функции вблизи определенной точки. Когда говорят о пределе функции, то подразумевают, что значение функции приближается к определенному числу, к которому она стремится в пределе. В данной статье мы рассмотрим случай, когда предел функции равен 0.
Предел функции равен 0 означает, что значение функции становится все ближе к нулю, когда аргумент приближается к определенной точке. Это означает, что независимо от того, насколько малым мы будем принимать значение функции, мы всегда сможем найти такое значение аргумента, при котором функция будет иметь значение, близкое к нулю.
Значение предела функции, равного 0, может иметь различные интерпретации в разных областях математики и наук: в теории вероятностей и статистике, физике и экономике. Например, в теории вероятности и статистике предел функции равный 0 означает, что вероятность события стремится к нулю в пределе, что свидетельствует о малой возможности этого события.
Таким образом, понятие предела функции равного 0 играет важную роль в различных областях математики и наук, а его значение может иметь различные интерпретации. Знание этого понятия и его значений позволяет более глубоко и точно анализировать поведение функций и решать различные задачи в различных областях знаний.
Предел функции: основы

Предел функции обозначается символом lim и записывается в виде:
lim(x→a)f(x) = L
где x – независимая переменная, a – точка приближения, f(x) – функция, L – предельное значение, к которому функция стремится при приближении к точке a.
Если для любого предельного значения L существует такое число δ, что для всех x, отличных от a, и удовлетворяющих условию 0<|x-a|<δ, выполняется неравенство |f(x)-L|<ε, где ε – произвольное положительное число, то говорят, что функция f(x) имеет предел L при x, стремящемся к a, и пишут:
lim(x→a)f(x) = L
Если предел функции существует и равен L, то говорят, что функция имеет конечный предел при a, и этот предел равен L. Если предел функции не существует или равен бесконечности, говорят, что предел функции бесконечный.
Определение предела функции позволяет решать различные математические задачи, включая вычисление производных, интегралов и нахождение асимптот функций.
Предел функции: определение и свойства
Определение предела функции можно сформулировать следующим образом: пусть задана функция f(x), определенная на некоторой окрестности точки c, за исключением, возможно, самой точки c. Если для любого положительного числа ε существует положительное число δ, такое что для всех x, удовлетворяющих условию 0
Некоторые свойства предела функции:
- Предел функции, если он существует, единственный.
- Если предел функции равен числу L, то предел обратной функции равен 1/L.
- Если предел функции при x, стремящемся к c, равен L, то пределы односторонних функций при x, стремящемся к c, также равны L.
- Если предел одностороннего предела функции при x, стремящемся к c, равен L, то предел функции при x, стремящемся к c, также равен L.
Анализ пределов функций играет важную роль в решении различных математических задач. Он позволяет определить, сходится ли функция к определенному значению в заданной точке, а также описать особенности ее поведения на границах области определения.
Геометрический смысл предела функции
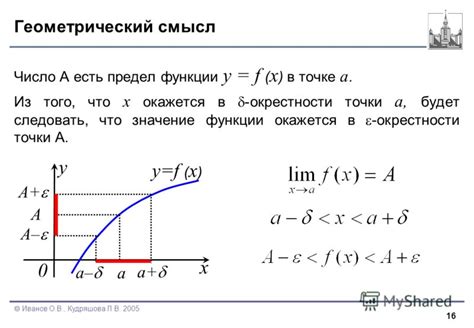
Геометрический смысл предела функции заключается в понятии приближения точки на графике функции к определенной предельной точке. Предел функции можно интерпретировать как значение, к которому стремится функция при движении ее аргумента ближе и ближе к определенной точке. Графически говоря, предел функции равен 0 означает, что график функции приближается к оси OY (ось ординат) или имеет горизонтальную асимптоту на уровне 0.
Определение предела функции на бесконечности
Определение предела функции на бесконечности основывается на понятии бесконечности. Если функция f(x) стремится к некоторому конечному пределу L при x, стремящемся к бесконечности, то говорят, что предел функции f(x) при x, стремящемся к бесконечности, равен L.
Формально, для любого положительного числа ε (эпсилон) существует положительное число M, такое что для всех значений x, больших M, выполняется |f(x) - L|
Это означает, что существует такая окрестность вокруг L, в которой все значения функции f(x), где x больше M, находятся. То есть, при достаточно больших значениях x, функция f(x) будет очень близка к L.
Определение предела функции на бесконечности играет важную роль в математическом анализе и может использоваться для изучения поведения функции на «бесконечности». Оно позволяет определять, каким будет значением функции, когда ее аргумент стремится к бесконечности, и как функция себя ведет в таких условиях.
Например, функция f(x) = 1/x имеет предел 0 при x, стремящемся к плюс или минус бесконечности. Это можно сформулировать следующим образом: предел функции f(x) при x, стремящемся к плюс или минус бесконечности, равен 0.
Определение предела функции на бесконечности позволяет проводить анализ функций и изучать их поведение на «краю» области определения. Это важный инструмент математического анализа и широко применяется в различных областях науки и техники.
Предел функции равен 0: понятие и примеры

Приведем несколько примеров функций, у которых предел равен 0:
| Пример | Функция | Предел |
|---|---|---|
| 1 | f(x) = 1/x | предел при x → ∞ равен 0 |
| 2 | f(x) = sin(x)/x | предел при x → 0 равен 0 |
| 3 | f(x) = 1/x2 | предел при x → ±∞ равен 0 |
В первом примере функция f(x) = 1/x стремится к нулю, когда аргумент x стремится к бесконечности. Во втором примере функция f(x) = sin(x)/x приближается к нулю, когда x стремится к нулю. В третьем примере функция f(x) = 1/x2 стремится к нулю, как при x → +∞, так и при x → -∞.
Знание и понимание пределов функций равных нулю позволяет анализировать поведение функции в окрестности различных точек и применять это знание в решении множества математических задач.
Предел функции на расширенной числовой оси
Предел функции на расширенной числовой оси представляет собой особый случай понятия предела функции, когда функция стремится к бесконечности или отрицательной бесконечности.
Для определения предела функции на расширенной числовой оси используется символ бесконечности (∞). Если функция f(x) стремится к бесконечности при приближении аргумента x к некоторому значению a, записывается предел "f(x) → ∞ при x → a". Аналогично, если функция f(x) стремится к отрицательной бесконечности при приближении аргумента x к a, записывается предел "f(x) → -∞ при x → a".
Предел функции на расширенной числовой оси определяется аналогично пределу функции на числовой прямой. Функция f(x) стремится к бесконечности при приближении x к a if для любого положительного числа M существует такое число δ, что для всех x, удовлетворяющих условию 0 M.
Аналогично, функция f(x) стремится к отрицательной бесконечности при приближении x к a if для любого отрицательного числа M существует такое число δ, что для всех x, удовлетворяющих условию 0
Предел функции на расширенной числовой оси играет важную роль в математическом анализе и используется для исследования поведения функций в окрестности особых точек.
Применение понятия предела функции в математике и физике

В математике предел функции используется, чтобы понять поведение функции в окрестности определенной точки. Он позволяет определить, как значение функции изменяется, когда ее аргумент приближается к определенному значению. Математическая концепция предела предоставляет общий метод анализа и понимания функций и их свойств в различных ситуациях.
В физике понятие предела функции также находит применение. Физические законы и явления описываются с помощью математических моделей, которые включают функции, выражающие зависимость физических величин друг от друга. Для анализа и прогнозирования этих зависимостей необходимо знать поведение функций в различных точках. Например, для определения скорости изменения величины с течением времени необходимо найти предел функции, описывающей эту зависимость.
Применение понятия предела функции в физике позволяет решать конкретные задачи, такие как определение максимального или минимального значения физической величины, нахождение точки перегиба графика функции, анализ стабильности системы и т. д. Кроме того, понятие предела имеет большое значение в понимании принципов и законов физики и способствует развитию научного мышления.
Выводя связь между математикой и физикой с помощью понятия предела функции, становится ясно, что эта математическая концепция является мощным инструментом для анализа, моделирования и понимания различных явлений и процессов в науке.








