Матрицы играют важную роль в математике и других областях науки. Их построение и анализ являются основными инструментами для решения различных задач. Матрицы представляют собой прямоугольные таблицы, состоящие из элементов, которые могут быть числами, переменными или функциями.
Основное понятие в матричном анализе - размерность матрицы. Она характеризует количество строк и столбцов матрицы. Размерность матрицы обозначается числами в формате MxN, где M - количество строк, а N - количество столбцов. Например, матрица размерности 3x2 имеет 3 строки и 2 столбца.
Существуют различные методы построения матриц. Один из них - использование элементарных операций над матрицами, таких как сложение, вычитание и умножение. Эти операции позволяют объединять матрицы и выполнять различные преобразования. Также можно применять матричные операции для решения систем линейных алгебраических уравнений и других задач.
Матрицы являются основой для различных математических концепций и моделей. Они используются в линейной алгебре, теории графов, теории вероятностей и других областях. Построение и анализ матриц позволяет упростить сложные вычисления и найти решения задач, которые были бы трудны в других формах представления данных.
Что такое матрица и ее основные характеристики

Основные характеристики матрицы включают:
- Размерность: определяет количество строк и столбцов матрицы.
- Элементы: числа, расположенные в матрице.
- Строки: горизонтальные элементы матрицы.
- Столбцы: вертикальные элементы матрицы.
- Главная диагональ: элементы матрицы, расположенные от левого верхнего угла до правого нижнего угла.
- Ведущий элемент: элемент матрицы, который расположен в левом верхнем углу.
- Транспонированная матрица: матрица, полученная путем замены строк на столбцы и столбцов на строки.
- Единичная матрица: квадратная матрица, у которой на главной диагонали стоят единицы, а остальные элементы равны нулю.
- Нулевая матрица: матрица, все элементы которой равны нулю.
Матрицы могут быть использованы для представления различных данных, например, для описания систем уравнений, задач оптимизации или для графического программирования. Изучение и использование матриц позволяет применять методы линейной алгебры для решения сложных задач.
Применение матриц в различных областях
Одной из основных областей, где матрицы активно используются, является линейная алгебра. Они позволяют оперировать с векторами и решать системы линейных уравнений. Также матрицы применяются в линейном программировании для поиска оптимальных решений задачи с ограничениями.
Матрицы находят применение в компьютерной графике и анимации. Они используются для представления трехмерных моделей и преобразования их координат. Матрицы позволяют осуществлять трансляцию, масштабирование и поворот объектов.
В статистике матрицы применяются для анализа данных, вычисления корреляции и регрессии. Они позволяют сжать информацию и находить зависимости между переменными.
Матрицы находят применение в теории графов, где описывают связи между вершинами и ребрами. Они позволяют решать задачи нахождения кратчайшего пути, поиска циклов и определения структуры графа.
Матрицы используются в физике для описания физических процессов и состояний системы. Они позволяют моделировать движение частиц, электрические и магнитные поля, а также волновые процессы.
Кроме указанных областей, матрицы применяются в экономике, биологии, искусственном интеллекте, криптографии и других областях. Их гибкость и универсальность делают матрицы незаменимым инструментом в решении разнообразных задач.
Таким образом, применение матриц распространено во многих научных и прикладных областях. Они позволяют удобно организовывать данные и выполнять операции над ними, а также находить зависимости и решать задачи в различных областях знаний.
Размерность матрицы и ее связь с количеством переменных

В матричной форме, система линейных уравнений может быть выражена как умножение матрицы коэффициентов на вектор переменных. Размерность этой матрицы определяется количеством переменных в системе уравнений.
Например, если система уравнений содержит 3 переменных, то матрица коэффициентов будет иметь 3 столбца, каждый из которых соответствует одной переменной. Каждая строка матрицы представляет собой одно уравнение системы.
Таким образом, размерность матрицы связана с количеством переменных в системе уравнений. Чтобы обеспечить согласованность размерностей, матрица коэффициентов должна иметь столько же столбцов, сколько и переменных, а количество строк будет равно количеству уравнений в системе.
Правильное определение размерности матрицы является важным шагом при построении и решении системы уравнений. Оно позволяет устанавливать соответствие между переменными и уравнениями, что обеспечивает корректную обработку данных при проведении матричных операций.
Операции над матрицами: сложение, вычитание, умножение
В математике операции над матрицами выполняются с использованием различных методов и правил. Основные операции над матрицами включают сложение, вычитание и умножение.
Сложение матриц выполняется путем покомпонентного сложения соответствующих элементов матриц. Для сложения двух матриц необходимо, чтобы они были одинакового размера. Результатом сложения будет новая матрица того же размера, у которой каждый элемент равен сумме соответствующих элементов исходных матриц.
Вычитание матриц также выполняется путем покомпонентного вычитания соответствующих элементов матриц. Аналогично сложению, для вычитания двух матриц они должны быть одинакового размера. Результатом вычитания будет новая матрица того же размера, у которой каждый элемент равен разности соответствующих элементов исходных матриц.
Умножение матриц является более сложной операцией. Здесь каждый элемент новой матрицы получается путем умножения элементов соответствующей строки первой матрицы на элементы соответствующего столбца второй матрицы, а затем сложения полученных произведений. Умножение матриц возможно только при выполнении условия: количество столбцов первой матрицы должно быть равно количеству строк второй матрицы.
Операции над матрицами широко применяются в различных областях науки и техники. Например, в линейной алгебре, численных методах, теории вероятностей и в других математических дисциплинах. Знание основных операций над матрицами позволяет эффективно работать с множеством данных и решать широкий спектр задач.
| Сложение матриц | Вычитание матриц | Умножение матриц | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
Транспонирование матрицы и его значение

Транспонирование матрицы имеет несколько важных применений:
- Передача данных: транспонирование матрицы используется для перекодировки информации при передаче данных между системами.
- Математические операции: транспонирование матрицы активно применяется при выполнении операций с матрицами, таких как сложение, вычитание и умножение.
- Линейные преобразования: транспонирование матрицы используется для нахождения обратной матрицы и решения систем линейных уравнений.
Процесс транспонирования матрицы можно представить следующим образом:
- Создать новую матрицу с размерами, обратными исходной матрице.
- Заполнить новую матрицу значениями, поменяв местами строки и столбцы исходной матрицы.
Транспонирование матрицы не меняет ее ранг, определитель и собственные значения, но меняет собственные векторы. Кроме того, для квадратных матриц транспонированная матрица является симметричной.
Способы построения матрицы по заданным данным
Существует несколько способов построения матрицы по заданным данным. Один из простейших способов – это задать все элементы матрицы явно.
Например, можно задать матрицу размером 3x3 с элементами:
1 2 3
4 5 6
7 8 9
Также матрицу можно построить с помощью алгоритма или формулы:
Для примера, рассмотрим построение матрицы размером 2x2 с использованием формулы:
Элемент матрицы находится как результат применения определенной формулы к его координатам в матрице.
Например, заданная формула для элемента матрицы с координатами (i, j):
элемент(i,j) = i + j
Используя эту формулу, можно построить матрицу:
0 1
1 2
Также, матрицу можно построить заполнив ее элементы шаблоном или комбинируя разные способы исходя из заданных условий.
Важно учитывать, что строительные способы матрицы могут варьироваться в зависимости от задачи и требуемого результата. Поэтому для каждой конкретной задачи следует выбирать оптимальный способ построения матрицы, учитывая доступные данные и требуемые условия.
Специальные виды матриц: единичная, нулевая, диагональная
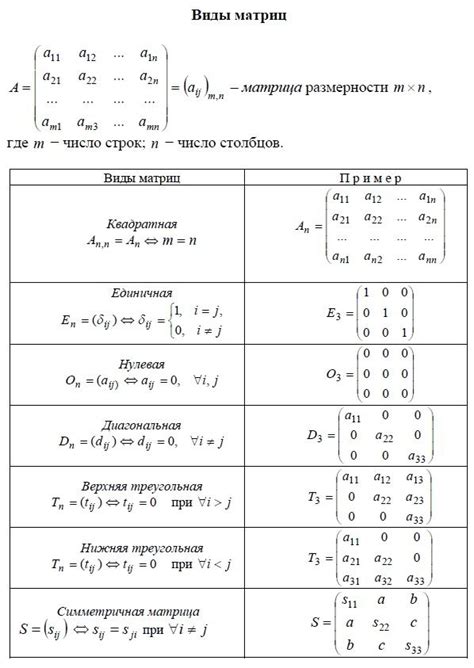
Специальные виды матриц часто применяются в различных областях математики и программирования. Они имеют определенные свойства, которые делают их полезными при решении конкретных задач.
Единичная матрица является квадратной матрицей, у которой на главной диагонали стоят единицы, а остальные элементы равны нулю. Обозначается символом E или I. Например, единичная матрица размером 3x3 будет выглядеть следующим образом:
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Нулевая матрица состоит из элементов, равных нулю. Это матрица, у которой все элементы равны нулю. Обозначается символом O или 0. Например, нулевая матрица размером 2x2 будет выглядеть следующим образом:
| 0 | 0 |
| 0 | 0 |
Диагональная матрица имеет ненулевые элементы только на главной диагонали, а все остальные элементы равны нулю. Обозначается символом D. Например, диагональная матрица размером 3x3 будет выглядеть следующим образом:
| 2 | 0 | 0 |
| 0 | 4 | 0 |
| 0 | 0 | 7 |
Специальные виды матриц играют важную роль при решении систем линейных уравнений, нахождении собственных значений и векторов, а также в других математических операциях и алгоритмах.
Матрицы и линейные преобразования
Линейные преобразования обладают важным свойством: они сохраняют сумму векторов и умножение вектора на скаляр. Если A и B - матрицы, а k - скаляр, то для линейного преобразования T выполняется:
| T(A + B) = T(A) + T(B) |
| T(kA) = kT(A) |
Запись линейного преобразования в виде матрицы осуществляется следующим образом. Пусть дано линейное преобразование T: Rn → Rm и A = [aij] - матрица размерности m × n, где каждый элемент aij является коэффициентом преобразования. Тогда T(x) = Ax, где x - вектор-столбец размерности n × 1.
Вычисление суммы и произведения матриц выполняется по следующим правилам:
| A + B = [aij + bij] |
| kA = [kaij] |
| AB = [cij], где cij = ∑nk=1aikbkj |
Матрицы также могут использоваться для решения систем линейных уравнений и нахождения собственных значений и собственных векторов. Кроме того, с их помощью можно описывать геометрические преобразования, такие как сдвиг, масштабирование, вращение и проекция.








