Параметрическое уравнение - это способ задания геометрических объектов в пространстве, основанный на использовании параметров. Параметр представляет собой числовое значение, которое изменяется в определенном диапазоне, и при каждом его изменении значения координат точки геометрического объекта также меняются. Таким образом, параметрическое уравнение позволяет описать сложные кривые и поверхности с использованием простых уравнений.
Основные понятия, связанные с параметрическим уравнением, - это параметрически заданная кривая и параметрически заданная поверхность. Параметрически заданная кривая - это кривая в пространстве, координаты точек которой выражаются через параметры. Например, уравнение параметрически заданной кривой может иметь вид x(t) = f(t), y(t) = g(t), где x и y - координаты точек кривой, а f(t) и g(t) - функции, определяющие координаты точек кривой через параметр t.
Пример параметрически заданной кривой - окружность. Уравнение окружности в параметрической форме имеет вид x(t) = r*cos(t), y(t) = r*sin(t), где r - радиус окружности, а t - параметр, изменяющийся от 0 до 2π.
Параметрически заданная поверхность - это поверхность в пространстве, координаты точек которой определяются через параметры. Например, уравнение параметрически заданной поверхности может иметь вид x(u, v) = f(u, v), y(u, v) = g(u, v), z(u, v) = h(u, v), где x, y и z - координаты точек поверхности, a f(u, v), g(u, v) и h(u, v) - функции, определяющие координаты точек поверхности через параметры u и v.
Пример параметрически заданной поверхности - сфера. Уравнение сферы в параметрической форме имеет вид x(u, v) = r*cos(u)*sin(v), y(u, v) = r*sin(u)*sin(v), z(u, v) = r*cos(v), где r - радиус сферы, а u и v - параметры, изменяющиеся от 0 до 2π и от -π/2 до π/2 соответственно.
Параметрическое уравнение широко используется в математике, физике, компьютерной графике и других областях науки. Оно позволяет описывать геометрические объекты более гибко и точно, чем традиционные уравнения. Кроме того, параметрическое уравнение обладает рядом других полезных свойств, таких как возможность легкого вычисления длины кривой, площади поверхности, векторного дифференцирования и интегрирования, а также решения сложных геометрических задач.
Определение параметрического уравнения

Параметры – это величины, которые могут принимать любые значения, задаваемые внешними условиями. Переменные, с другой стороны, зависят от параметров и могут принимать различные значения в зависимости от значений параметров.
Параметрическое уравнение часто используется для описания кривых и поверхностей в пространстве. Например, когда мы хотим описать траекторию движения объекта, мы можем использовать параметры времени и задать параметрическое уравнение для координат объекта в зависимости от времени.
Одним из преимуществ параметрического уравнения является его гибкость и возможность описывать сложные формы. Параметры позволяют нам легко варьировать форму и положение кривой или поверхности без необходимости изменять само уравнение.
Например, для описания окружности можно использовать параметрическое уравнение:
x = r * cos(t)
y = r * sin(t)
Где r – радиус окружности, а t – параметр, принимающий значения от 0 до 2π, которые описывают угол поворота точки на окружности.
Основные понятия параметрического уравнения
Основными понятиями параметрического уравнения являются:
- Параметр - переменная величина, которая определяет положение или форму фигуры. Параметры представляются с помощью обозначений, например, t, s, u.
- Параметрические уравнения - уравнения, в которых значения координат точки представлены в виде выражений с использованием параметров. Например, x = f(t), y = g(t), где x и y - координаты точки, а f(t) и g(t) - функции, зависящие от параметра t.
- Параметрическая кривая - график параметрического уравнения, представляющий собой множество точек, значения координат которых определяются значениями параметра. Параметрическая кривая может иметь различные формы, такие как прямые линии, окружности, эллипсы.
- Диапазон параметров - интервал или множество значений, которые может принимать параметр. Определение диапазона параметров позволяет ограничить область изменения координат точек фигуры.
Параметрическое уравнение широко используется в математике, физике, компьютерной графике и других областях. Оно позволяет более гибко задавать и анализировать геометрические объекты, а также моделировать их движение и изменение формы.
Параметрические уравнения в математике
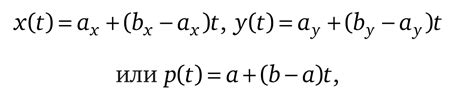
Параметрические уравнения удобны в тех случаях, когда кривая или поверхность не могут быть выражены в виде явных функций или когда требуется описать кривую с помощью параметров, например, для анимации или моделирования.
Параметрические уравнения широко применяются в математике, физике, компьютерной графике и многих других областях. Они позволяют описывать и анализировать сложные геометрические объекты, такие как эллипсы, параболы, гиперболы, спирали, поверхности в пространстве и даже трехмерные модели.
Примеры параметрических уравнений:
- Для окружности с центром в точке (a, b) и радиусом r:
- x = a + r * cos(t)
- y = b + r * sin(t)
- Для параболы:
- x = t
- y = t^2
- Для эллипса с полуосями a и b:
- x = a * cos(t)
- y = b * sin(t)
В параметрических уравнениях параметр t может принимать значения в определенном диапазоне, что позволяет описывать кривые с различными свойствами. Изменение значения параметра t влияет на положение точки на кривой или поверхности, что делает параметрические уравнения мощным инструментом для исследования геометрических объектов.
Преимущества параметрического уравнения
- Гибкость: Параметрическое уравнение позволяет менять значения параметров и тем самым изменять форму и положение кривой или поверхности. Это позволяет получать различные варианты из одного и того же уравнения.
- Описание сложных форм: Параметрическое уравнение позволяет описать сложные геометрические формы, такие как эллипсы, гиперболы и спирали, которые не могут быть описаны при помощи классических алгебраических уравнений.
- Удобство работы с параметрами: Параметрическое уравнение позволяет выразить координаты точек на кривой или поверхности через простые функции параметров. Это значительно облегчает проведение вычислений и анализ кривых и поверхностей.
- Интуитивность: Параметрическое уравнение легко представить графически, что позволяет наглядно увидеть форму или движение кривой или поверхности при изменении параметров.
Использование параметрических уравнений является важным инструментом во многих областях науки и техники, включая физику, математику, компьютерную графику, механику и другие. Они позволяют моделировать и анализировать сложные объекты и явления, а также предсказывать их поведение.
Примеры использования параметрического уравнения
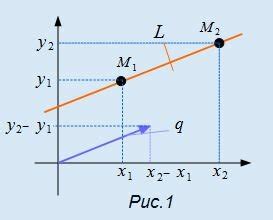
1. Геометрия: Параметрические уравнения широко используются для описания различных геометрических фигур. Например, параметрическое уравнение окружности может быть записано как:
x = r * cos(θ)
y = r * sin(θ)
где r - радиус окружности, а θ - угол.
2. Физика: Параметрические уравнения могут быть использованы для моделирования движения тел в пространстве. Например, параметрическое уравнение броска мяча в вертикальной плоскости может быть записано как:
x = v₀ * t
y = h₀ + v₀ * t + (1/2) * g * t²
где v₀ - начальная вертикальная скорость, h₀ - начальная высота, g - ускорение свободного падения, t - время.
3. Инженерия: В инженерных расчетах параметрические уравнения используются для определения различных параметров. Например, параметрическое уравнение может быть использовано для определения величины сопротивления цепи в зависимости от различных входных параметров, таких как сопротивления, емкостей, индуктивностей и частоты.
Это только некоторые примеры использования параметрического уравнения. Этот подход очень гибок и может быть применен в различных областях для решения различных задач.
Кривые, заданные параметрическим уравнением
Кривая, заданная параметрическим уравнением, представлена в виде векторной функции r(t) = (x(t), y(t)) или r(t) = (x(t), y(t), z(t)), где t - параметр, изменяющийся в некотором интервале.
Параметры x(t), y(t) и z(t) определяются как функции от t и определяют координаты точки на кривой. Кривая может быть задана явным образом, когда каждая координата выражена через t, или неявным образом, когда выражения для координат содержатся внутри других функций или уравнений.
Параметрическое уравнение позволяет описать различные кривые, такие как окружность, эллипс, парабола, гипербола и другие. Например, параметрическое уравнение окружности задается как x(t) = r cos(t), y(t) = r sin(t), где r - радиус окружности, а t изменяется от 0 до 2π.
Координаты точек на параметрической кривой

Для параметрического уравнения, принимающего вид x = f(t) и y = g(t), координаты точек на кривой определяются подстановкой различных значений параметра. Таким образом, для каждого t получаем значения x и y, которые задают точку на кривой.
Примером параметрической кривой может служить окружность с радиусом R и центром в начале координат. Ее параметрическое уравнение задается следующим образом:
x = R * cos(t)
y = R * sin(t)
Где t пробегает значения от 0 до 2π (или от 0 до 360°). Подставляя различные значения t в эти уравнения, можно получить координаты точек, лежащих на окружности.
Например, при t = 0 получим x = R и y = 0, что соответствует точке (R, 0) на окружности. При t = π/2, получим x = 0 и y = R, что соответствует точке (0, R) и так далее.
Графическое представление параметрического уравнения
Графическое представление параметрического уравнения позволяет визуализировать зависимость двух величин в зависимости от одного или нескольких параметров. Оно используется для изучения графических свойств функций, исследования их поведения и решения различных задач.
Для построения графика параметрического уравнения вводятся значения параметра в определенном диапазоне, после чего находятся соответствующие значения остальных переменных. Полученные значения используются для построения точек на координатной плоскости.
Один из способов представления графика параметрического уравнения - использование таблицы, где в одном столбце перечисляются значения параметра, а в соседнем столбце соответствующие значения остальных переменных. Затем эти значения можно соединить линиями, получив график функции.
| Параметр t | X | Y |
|---|---|---|
| t1 | X(t1) | Y(t1) |
| t2 | X(t2) | Y(t2) |
| t3 | X(t3) | Y(t3) |
| ... | ... | ... |
На основе полученной таблицы значений можно провести график, отметив на координатной плоскости соответствующие точки. После этого можно аппроксимировать полученные точки гладкой кривой или закрашивать область между точками.
Графическое представление параметрического уравнения позволяет наглядно исследовать его свойства, такие как периодичность, симметрию, пересечения с осями координат и другими кривыми. Также оно удобно для сравнения различных параметров и выявления закономерностей в их влиянии на график функции.
Решение параметрического уравнения
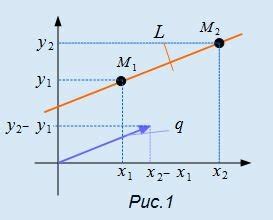
Для решения параметрического уравнения необходимо найти значения параметров, при которых оно выполняется. Решение параметрического уравнения может быть представлено в виде набора уравнений, связывающих значения параметров.
Основной метод решения параметрического уравнения заключается в приведении его к системе обыкновенных дифференциальных уравнений или к системе алгебраических уравнений. Затем решается полученная система уравнений для определения значений параметров.
Примером параметрического уравнения может служить уравнение движения тела по баллистической траектории:
x = v₀·t·cos(θ)
y = v₀·t·sin(θ) - (g·t²)/2
где x и y - координаты тела в зависимости от времени t и параметров начальной скорости v₀ и угла броска θ, а g - ускорение свободного падения.
Для решения данного параметрического уравнения можно использовать метод численного интегрирования, например, метод Эйлера или метод Рунге-Кутта. При нахождении значений координат x и y в заданные моменты времени можно определить траекторию движения тела.
Применение параметрического уравнения в физике и других науках
В физике параметрические уравнения применяются для моделирования и анализа движения тел, в том числе точек, маятников, спутников и других объектов. Например, движение точки в трехмерном пространстве может быть описано параметрическими уравнениями, в которых значения x, y и z зависят от времени t. Это позволяет точно предсказывать положение и скорость объекта в любой момент времени.
Также параметрические уравнения используются для моделирования и анализа колебаний и волн. Например, гармонические колебания могут быть описаны параметрическими уравнениями, в которых значения x и y представляют собой синус и косинус соответственно, а параметр t представляет время.
В других науках, таких как экономика, биология и социология, параметрические уравнения используются для анализа различных процессов и явлений. Например, экономические модели могут быть описаны параметрическими уравнениями, в которых значения x, y и z представляют различные экономические показатели, а параметр t представляет время.
Применение параметрического уравнения в науках позволяет более точно описывать и предсказывать различные процессы и явления. Оно также облегчает математический анализ и моделирование сложных систем и объектов. Поэтому знание параметрического уравнения является важным инструментом для ученых и исследователей в различных областях науки.








