В математике неравенство - это утверждение о том, что одно выражение больше или меньше другого. Неравенства широко применяются в различных областях науки, экономике, физике и других сферах, чтобы выразить ограничения и связи между переменными.
Однако не все неравенства имеют решение. Существуют неравенства, для которых не существует ни одного значения, удовлетворяющего его условию. Такие неравенства называются неразрешимыми. Но на самом деле многие неравенства имеют единственное решение, то есть существует только одно значение, которое удовлетворяет условиям неравенства.
Примером неравенства с единственным решением может служить неравенство вида "2x + 3 < 7". Чтобы найти решение данного неравенства, следует выразить переменную x и убедиться, что это значение удовлетворяет условию неравенства. В данном случае, сокращая выражение, получим "2x < 4", а затем "x < 2". То есть, единственным решением данного неравенства является любое значение x, которое меньше 2.
Подводя итог, неравенство имеет единственное решение, когда существует только одно значение, удовлетворяющее условию неравенства. Примером такого неравенства может служить "2x + 3 < 7", где решением является x < 2. Важно уметь выражать переменные и проверять их значения, чтобы определить единственность решения неравенства.
Неравенство имеет единственное решение:

Неравенство имеет единственное решение, когда неравенство справедливо только для одного значения переменной. В таком случае можно указать точное значение или диапазон значений, при которых неравенство выполняется.
Например, рассмотрим неравенство:
- x + 3 ≤ 7
Здесь переменная x должна быть меньше или равна 4, чтобы неравенство было выполнено. Таким образом, уравнение имеет единственное решение x = 4.
Другой пример:
- 2y - 5 ≥ 7
В данном случае значение переменной y должно быть больше или равно 6, чтобы неравенство было справедливым. Таким образом, уравнение имеет единственное решение y = 6.
Таким образом, неравенство имеет единственное решение, когда можно указать точное значение переменной или диапазон значений, при которых неравенство справедливо.
Понятие неравенства
Неравенства используются для представления сравнений между числами или выражениями. Они могут иметь различные знаки, такие как "больше" (>) или "меньше" (=" (больше или равно) или "
Примеры неравенств:
- 5 > 3 (пять больше трех)
- 2 + 3
- 4 >= 4 (четыре больше или равно четыре)
- 8 - 2
Неравенства могут использоваться в различных областях математики и науки для сравнения, классификации и решения проблем. Они также могут использоваться для определения диапазона значений переменных или выражений и установления отношений между ними.
Примеры неравенств

Вот несколько примеров неравенств:
1. x + 5 > 10
Это неравенство говорит нам, что значение выражения x + 5 больше 10. Например, если x = 4, то 4 + 5 = 9, что меньше 10 и неравенство не выполняется. Но если x = 6, то 6 + 5 = 11, что больше 10 и неравенство выполняется.
2. 2y ≤ 8
Это неравенство говорит нам, что значение выражения 2y не превышает 8. Например, если y = 3, то 2 * 3 = 6, что меньше 8 и неравенство выполняется. А если y = 5, то 2 * 5 = 10, что больше 8 и неравенство не выполняется.
3. z - 1
Это неравенство говорит нам, что значение выражения z - 1 меньше значения выражения 2z + 3. Например, если z = 4, то 4 - 1 = 3, а 2 * 4 + 3 = 11, что подтверждает неравенство. Но если z = 1, то 1 - 1 = 0, а 2 * 1 + 3 = 5, что не выполняет неравенство.
Это всего лишь некоторые примеры неравенств, которые используются в математике для сравнения числовых значений, переменных или выражений.
Свойства неравенств
Важно понимать, что неравенство имеет свои свойства, которые можно использовать при решении уравнений.
- Транзитивность: Если a > b и b > c, то a > c. Это свойство позволяет нам сравнивать несколько чисел между собой, используя знаки ">", " 3 и 3 > 1, то мы можем заключить, что 5 > 1.
- Добавление и вычитание: Если a > b, то a + c > b + c и a - c > b - c. Мы можем добавить или вычесть одно и то же число с обеих сторон неравенства, и неравенство все равно будет справедливым. Например, если 4 > 2, то мы можем заключить, что 4 + 3 > 2 + 3.
- Умножение и деление на положительные числа: Если a > b и c > 0, то a * c > b * c и a / c > b / c. Мы можем умножить или разделить обе части неравенства на положительное число, и неравенство все равно будет справедливым. Например, если 3 > 2 и 4 > 0, то мы можем заключить, что 3 * 4 > 2 * 4.
- Умножение и деление на отрицательные числа: Если a > b и c 3 и -2
Эти свойства неравенств помогают нам анализировать и решать математические задачи, связанные с неравенствами.
Методы решения неравенств
Для решения неравенств существуют различные методы, которые позволяют найти и описать множество всех значений переменной, удовлетворяющих данному неравенству.
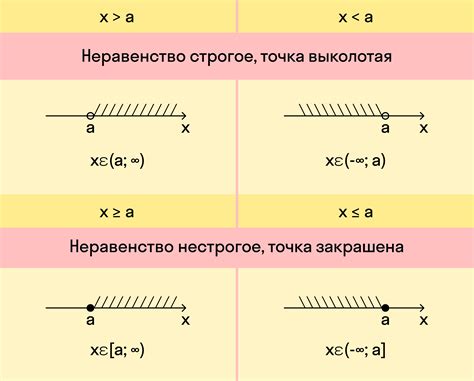
Метод графика. Один из наиболее простых и понятных способов решения неравенства. Уравнение неравенства переводится в графическую форму, после чего с помощью графика находится множество решений. Например, неравенство x > 2 может быть представлено на координатной плоскости с помощью графика прямой, которая проходит через точку (2, 0) и идет вправо.
Метод замены переменной. Неравенство преобразуется путем замены переменной на другую, более удобную для решения неравенства. Этот метод часто применяется при сложных математических выражениях, когда неравенство содержит степени, корни или логарифмы. Например, для решения неравенства x2 + 3x - 4 < 0 можно ввести новую переменную y = x + 2 и преобразовать неравенство к более простой форме y2 - 8 < 0, которую легче решить.
Метод интервалов. Неравенство представляется в виде интервала, который содержит все значения переменной, удовлетворяющие неравенству. Например, неравенство x > 3 может быть записано в виде интервала (3, +∞), где ( означает "не включая", а +∞ обозначает бесконечность.
Это лишь некоторые из методов решения неравенств. В зависимости от типа неравенства и его сложности, может потребоваться применение других методов, таких как метод декомпозиции неравенства, метод замены знаков и другие.
Применение неравенств в мире
Неравенства играют важную роль в различных областях человеческой жизни. Они присутствуют как в социальных и экономических отношениях, так и в науке и природе.
В социальном аспекте неравенства проявляются в виде различий в доступе к образованию, здравоохранению и возможностям трудоустройства. Неравенства между разными группами населения могут вести к социальному недовольству и конфликтам. Решение неравенств в данном случае связано с улучшением условий жизни, созданием равных возможностей и борьбой с дискриминацией.
В экономической сфере неравенства проявляются в виде различий в заработной плате, уровне доходов и богатства. Бедность и экономическое неравенство часто приводят к неравному распределению ресурсов, что затрудняет развитие стран и обществ. Решение этой проблемы требует разработки эффективных экономических политик, создания равных условий для всех участников рынка и борьбы с коррупцией.
Неравенства также присутствуют в научной и природной сфере. В науке они проявляются в виде неравного доступа к образованию и исследовательским ресурсам. В природе неравенства наблюдаются в виде различий в распределении живых организмов и природных ресурсов. Изучение и понимание этих неравенств помогает нам лучше понять мир вокруг нас и заботиться о его устойчивом развитии.
Таким образом, неравенства имеют широкое применение в различных сферах нашей жизни. Решение этих неравенств требует усилий со стороны индивидов, общества и государства, чтобы создать более справедливое и равноправное общество.
Роль неравенств в математике

Неравенства играют важную роль в математике, представляя собой один из основных инструментов для описания и анализа различных математических объектов и явлений. Они позволяют сравнивать величины и устанавливать отношения между ними.
В математическом анализе неравенства используются для определения условий сходимости и расходимости рядов, последовательностей и интегралов. Например, неравенство Коши-Буняковского-Шварца используется для доказательства неравенства треугольника в нормированном пространстве.
В линейной алгебре неравенства используются для решения систем линейных уравнений. С их помощью можно определить границы векторов и матриц и проводить сравнение линейных комбинаций.
В теории вероятностей неравенства играют важную роль при определении вероятностных оценок и установлении границ случайных величин.
Неравенства также находят применение в оптимизации, где с их помощью можно найти экстремумы функций и определить оптимальные значения переменных.
Математика неотделима от неравенств, которые являются одним из фундаментальных понятий и инструментов для понимания и изучения различных математических явлений и связей.








