Расстояние между двумя прямыми - это величина, которая показывает, насколько перпендикулярно одна прямая направлена к другой. Понимание этой концепции является важным в математике и физике, а также в других областях, где применяются прямые линии.
Для расчета расстояния между прямыми необходимо знать их уравнения. Первое уравнение прямой можно записать в виде y = mx + b, где m - это наклон прямой, а b - точка пересечения прямой с координатной осью y. Второе уравнение прямой записывается в виде y = nx + c, где n - это наклон второй прямой, а c - точка пересечения с координатной осью y.
Для нахождения расстояния между прямыми необходимо использовать формулу, которая основывается на их наклонах и точках пересечения:
Расстояние d между прямыми вычисляется по формуле:
d = |(c - b) / √(1 + m²)|
Где m и n - наклоны прямых, а b и c - точки пересечения с координатной осью y. Знак | | обозначает модуль числа, то есть абсолютное значение.
Как видно из формулы, расстояние между прямыми зависит от их наклонов и точек пересечения. Чем ближе эти значения к нулю, тем меньше будет расстояние между прямыми.
Основные понятия расстояния между прямыми
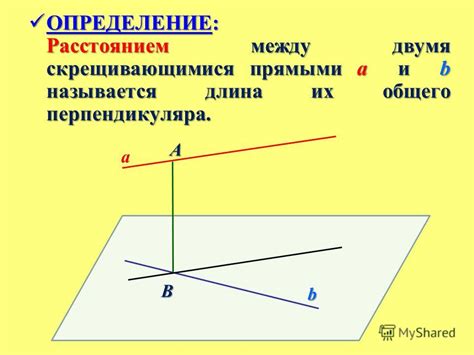
Существует несколько методов расчета расстояния между прямыми в зависимости от их задания. Одним из наиболее распространенных является метод, основанный на вычислении расстояния между проекциями точки на прямую. Пусть даны две прямые, заданные уравнениями l1: a1x + b1y + c1 = 0 и l2: a2x + b2y + c2 = 0. Необходимо найти расстояние между этими прямыми.
- Найдем векторное произведение нормальных векторов каждой прямой: n1 = (a1, b1) и n2 = (a2, b2).
- Найдем точку P, через которую проведем перпендикуляр к обеим прямым. Для этого решим систему уравнений l1 и l2.
- Найдем вектор OP, где O - начало координат.
- Найдем проекцию вектора OP на нормальный вектор прямой l1. Это можно сделать, найдя скалярное произведение OP и n1, и разделив его на длину вектора n1.
- Результат будет являться искомым расстоянием между прямыми.
Также существуют другие методы для расчета расстояния между прямыми, которые используют геометрические преобразования и алгоритмы. Они обычно требуют более сложных вычислений, но могут использоваться в более сложных задачах, связанных с прямыми и их взаимодействием.
Прямая в пространстве
Прямая в пространстве представляет собой наименьшее измерение, у которого нет ширины и высоты. В пространстве прямая может быть определена двумя независимыми параметрами, обычно обозначаемыми как x и y.
Координаты точки на прямой могут быть представлены с помощью уравнения, известного как уравнение прямой. В пространстве уравнение прямой может быть записано в виде:
ax + by + cz + d = 0
где a, b и c - коэффициенты, а d - свободный член. Коэффициенты определяют направление прямой в пространстве.
Чтобы найти расстояние между двумя прямыми в пространстве, необходимо использовать известные методы расчета такие как нахождение ближайших точек или использование векторного представления прямых.
Векторное уравнение прямой

Векторное уравнение прямой используется для описания положения прямой в трехмерном пространстве. Оно имеет вид:
r = r0 + tu
где r - радиус-вектор любой точки на прямой, r0 - радиус-вектор одной из точек прямой, u - направляющий вектор прямой, t - параметр, пробегающий все действительные числа.
Направляющий вектор u задает направление прямой, а r0 определяет ее положение в пространстве.
Векторное уравнение прямой позволяет компактно описать все точки прямой и найти расстояние между прямыми.
Пример:
Даны две точки прямой: A(1, 2, 3) и B(4, 5, 6). Найдем направляющий вектор:
u = rB - rA = (4 - 1, 5 - 2, 6 - 3) = (3, 3, 3)
Выберем A(1, 2, 3) в качестве r0. Тогда векторное уравнение прямой будет выглядеть так:
r = (1, 2, 3) + t(3, 3, 3)
Таким образом, векторное уравнение прямой определяет все точки, лежащие на прямой, и может быть использовано для вычисления расстояния между прямыми.
Расстояние между точкой и прямой
Для расчета расстояния между точкой и прямой используется специальная формула, которая основана на геометрических правилах и свойствах прямых. Формула зависит от типа прямой и ее уравнений.
Если уравнение прямой задано в общем виде Ax + By + C = 0, а координаты точки (x0, y0), то расстояние между этой точкой и прямой можно вычислить по формуле:
d = |Ax0 + By0 + C| / sqrt(A^2 + B^2)
где d - искомое расстояние, A, B и C - коэффициенты уравнения прямой, x0 и y0 - координаты точки, sqrt - корень квадратный.
Если уравнение прямой задано в параметрической форме x = x1 + at, y = y1 + bt, где (x1, y1) - координаты точки прямой, a и b - произвольные числа, а t - параметр, то расстояние между точкой и прямой можно вычислить по формуле:
d = |(x0 - x1)a - (y0 - y1)b + t(y0 - y1)| / sqrt(a^2 + b^2)
где d - искомое расстояние, x0 и y0 - координаты точки, sqrt - корень квадратный.
Зная уравнение прямой и координаты точки, можно использовать соответствующую формулу для вычисления расстояния. Расстояние между точкой и прямой является положительным числом и показывает, насколько далеко точка находится от прямой.
Расстояние между параллельными прямыми

Если две прямые параллельны и не пересекаются, то расстояние между ними можно найти следующим образом:
- Выберите произвольную точку на одной из прямых.
- Проведите перпендикуляр от этой точки к другой прямой.
- Измерьте длину этого перпендикуляра.
Таким образом, длина перпендикуляра, проведенного от произвольной точки одной прямой к другой, будет равна расстоянию между этими прямыми.
Если известны координаты двух точек, лежащих на разных прямых, можно воспользоваться формулой расстояния между двумя точками:
d = √((x2 - x1)^2 + (y2 - y1)^2)
где d - расстояние между двумя точками, (x1, y1) - координаты первой точки, (x2, y2) - координаты второй точки.
Для нахождения расстояния между параллельными прямыми можно использовать эти формулы, учитывая, что прямые параллельны и, следовательно, имеют одинаковый угловой коэффициент.
Расстояние между скрещивающимися прямыми
Для определения расстояния между скрещивающимися прямыми можно использовать несколько методов:
- Метод перпендикуляров:
- Находим точку пересечения прямых;
- Строим перпендикуляр к одной из прямых, проходящий через точку пересечения;
- Измеряем расстояние от точки пересечения до перпендикуляра.
- Находим вектора, параллельные прямым;
- Находим нормальный вектор к этим векторам;
- Проектируем вектор между двумя прямыми на нормальный вектор;
- Измеряем длину проекции - это и будет расстоянием между прямыми.
- Подставляем уравнения прямых в систему уравнений;
- Решаем систему уравнений и находим точку пересечения прямых;
- Измеряем расстояние между точкой пересечения и каждой из прямых.
Выбор метода зависит от доступных данных и предпочтений. Каждый из методов может быть использован для определения расстояния между скрещивающимися прямыми, при условии, что известны координаты точек или уравнения этих прямых.
Метод проекций для определения расстояния
Для определения расстояния между прямыми применяется метод проекций. Этот метод основан на разложении вектора, соединяющего две произвольные точки на прямых, на две компоненты: одну, параллельную одной из прямых, и другую, перпендикулярную обоим прямым.
Для начала рассмотрим две прямые, заданные своими параметрическими уравнениями:
- Прямая 1: \(l_1: \vec{r}(t) = \vec{r_0} + t\vec{v_1}\)
- Прямая 2: \(l_2: \vec{r}(s) = \vec{r_0} + s\vec{v_2}\)
Здесь \(\vec{r}(t)\) и \(\vec{r}(s)\) - радиус-векторы точек прямых \(l_1\) и \(l_2\) соответственно, \(\vec{r_0}\) - радиус-вектор начальной точки обеих прямых, \(\vec{v_1}\) и \(\vec{v_2}\) - направляющие векторы прямых \(l_1\) и \(l_2\) соответственно, \(t\) и \(s\) - параметры.
Расстояние между прямыми можно определить следующим образом:
- Рассчитываем вектор \(\vec{D}\), соединяющий две произвольные точки прямых: \(\vec{D} = \vec{r}(t) - \vec{r}(s)\).
- Разлагаем вектор \(\vec{D}\) на две компоненты: \(\vec{D} = \vec{D_{\parallel}} + \vec{D_{\perp}}\), где \(\vec{D_{\parallel}}\) - компонента, параллельная одной из прямых, а \(\vec{D_{\perp}}\) - компонента, перпендикулярная обоим прямым.
- Расстояние между прямыми будет равно модулю компоненты \(\vec{D_{\perp}}\), то есть расстоянию от точки прямой \(l_1\), проекции которой на прямую \(l_2\) равна точке прямой \(l_2\).
Таким образом, метод проекций позволяет найти расстояние между прямыми, используя проекцию точек одной прямой на другую прямую.
Применение расстояния между прямыми в практических задачах
| Задача | Применение |
| Градостроительство | Расстояние между прямыми может использоваться для расчета безопасной дистанции между строениями или дорогами. |
| Автомобильная промышленность | Расстояние между прямыми может применяться для определения безопасного расстояния между движущимися автомобилями, обеспечивающего предотвращение аварий. |
| Строительство | При строительстве используются прямые линии, и знание расстояния между ними позволяет правильно выстраивать конструкции и обеспечивать их прочность. |
| Геодезия и картография | Расстояние между прямыми может использоваться для измерения расстояний на карте или в реальном мире, а также для построения точных карт и планов местности. |
| Физика | В физике расстояние между прямыми может применяться для анализа и моделирования движения объектов, в том числе маршрутов планет и комет. |
Это лишь некоторые из множества областей, в которых расстояние между прямыми находит свое применение. Важно понимать и уметь использовать эту величину для решения различных задач в реальной жизни.








