Найти общее решение системы линейных уравнений

Системы линейных уравнений являются важным понятием в математике и широко применяются в различных областях науки и техники. Нахождение их решений является одним из основных заданий, с которыми сталкиваются студенты и профессионалы. В этой статье мы рассмотрим процесс поиска общего решения системы линейных уравнений и предоставим детальный гайд, который поможет вам разобраться в этой теме на все сто процентов.

Для начала, давайте разберемся, что вообще такое система линейных уравнений. Это набор уравнений, в которых все неизвестные переменные входят линейно. В общем виде систему линейных уравнений можно представить как:

a₁⋅x₁ + a₂⋅x₂ + ... + aₙ⋅xₙ = b₁

a₁⋅x₁ + a₂⋅x₂ + ... + aₙ⋅xₙ = b₂

...

a₁⋅x₁ + a₂⋅x₂ + ... + aₙ⋅xₙ = bₘ

Где x₁, x₂, ..., xₙ - неизвестные переменные, a₁, a₂, ..., aₙ - коэффициенты перед этими неизвестными переменными, а b₁, b₂, ..., bₘ - константы.

Поиск общего решения системы линейных уравнений сводится к нахождению всех возможных значений неизвестных переменных, при которых все уравнения системы будут выполняться одновременно. Далее мы рассмотрим различные методы решения систем линейных уравнений и подробно объясним каждый из них.

Что такое система линейных уравнений

Система линейных уравнений может иметь различное количество уравнений и переменных. Например, система из двух уравнений может содержать две переменные. Решение системы линейных уравнений представляет собой набор значений переменных, при которых все уравнения системы выполняются.

Системы линейных уравнений широко применяются в различных областях науки и техники. Они используются для моделирования и анализа различных процессов, а также для решения задач оптимизации и принятия решений. Кроме того, системы линейных уравнений встречаются в математике как основной объект изучения в теории линейных уравнений и линейной алгебры.

Зачем нам нужно находить общее решение

Знание общего решения позволяет сделать следующие выводы:

• Определение совместности системы: Наличие общего решения говорит о совместности системы уравнений, то есть о возможности нахождения конкретных значений переменных, при которых все уравнения системы будут выполняться.
• Решение сложных задач: Общее решение системы линейных уравнений может быть использовано для решения более сложных математических и физических задач, когда требуется нахождение нескольких переменных, удовлетворяющих определенным условиям.
• Анализ системы: Из общего решения можно сделать выводы о свойствах системы, такие как её степень свободы или наличие определенных зависимостей между переменными.
• Проверка правильности результата: Найденное общее решение может быть использовано для проверки правильности результатов при решении системы уравнений с использованием численных методов или компьютерных алгоритмов.

В целом, нахождение общего решения системы линейных уравнений является важной и полезной математической операцией, которая позволяет решать различные задачи в науке, технике и повседневной жизни.

Нахождение общего решения системы линейных уравнений

Общее решение системы линейных уравнений представляет собой набор всех значений переменных, удовлетворяющих условиям системы. Для нахождения общего решения необходимо выполнить несколько шагов.

1. Привести систему к расширенной матрице, где уравнения записаны в виде строк, а переменные и свободные члены – в столбцах.
2. Применить элементарные преобразования строк, чтобы привести матрицу к ступенчатому виду.
3. Выразить главные переменные через свободные, чтобы получить общее решение системы.

Шаги подробнее:

1. Приведение системы к расширенной матрице:

   Систему линейных уравнений можно записать в виде расширенной матрицы. Например, система:

   a1x + b1y + c1z = d1

   a2x + b2y + c2z = d2

   a3x + b3y + c3z = d3

   можно представить в виде:

   | a1 b1 c1 | d1 |

   | a2 b2 c2 | d2 |

   | a3 b3 c3 | d3 |

2. Применение элементарных преобразований:

   С помощью элементарных преобразований расширенную матрицу можно привести к ступенчатому виду. Элементарные преобразования включают прибавление или вычитание одной строки к другой, умножение строки на скаляр и перестановку строк. Цель этого шага – сделать лидирующими ненулевые элементы в каждой строке. После этого система будет содержать только уравнения вида `x = ...`, где `x` – главная переменная, либо `0 = ...`, если соответствующая переменная свободная.

3. Выражение главных переменных через свободные:

   Выражение главных переменных через свободные – последний шаг для получения общего решения системы. Для этого необходимо одну за другой выразить главные переменные в каждом уравнении через свободные переменные. Это позволяет заполнить промежуточные промежутки между лидирующими единицами в матрице. Полученные выражения образуют общее решение системы линейных уравнений.

Нахождение общего решения системы линейных уравнений – важный этап решения задач, связанных с линейной алгеброй. Понимание этого процесса может помочь в решении разнообразных задач и нахождении численных значений переменных в системе линейных уравнений.

Шаг 1: Приведение системы к матричному виду

Для приведения системы к матричному виду необходимо выписать все коэффициенты перед неизвестными в системе линейных уравнений и записать их в виде матрицы коэффициентов. Также необходимо выписать правые части уравнений и записать их в виде столбца свободных членов.

Например, рассмотрим следующую систему линейных уравнений:

3x + 2y - z = 1

2x - y + 3z = 4

x + 3y + z = 2

Для приведения данной системы к матричному виду, мы выразим коэффициенты перед неизвестными и запишем их в матрицу следующим образом:

\[

A = \begin{bmatrix}

3 & 2 & -1 \\

2 & -1 & 3 \\

1 & 3 & 1 \\

\end{bmatrix}

\]

Также мы выразим правые части уравнений и запишем их в виде столбца свободных членов:

\[

B = \begin{bmatrix}

1 \\

4 \\

2 \\

\end{bmatrix}

\]

Таким образом, система линейных уравнений приводится к матричному виду в виде уравнения \[AX = B\], где \(A\) - матрица коэффициентов, \(X\) - вектор неизвестных, и \(B\) - столбец свободных членов.

Шаг 2: Приведение матрицы к ступенчатому виду

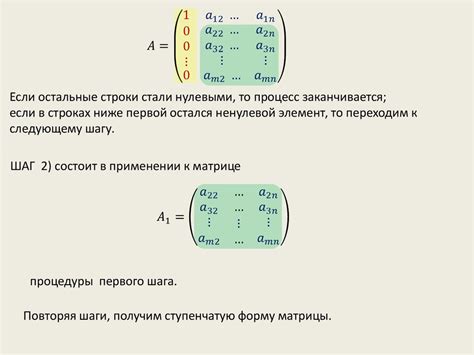
После описания системы линейных уравнений, следующий шаг в решении задачи состоит в приведении матрицы коэффициентов системы к ступенчатому виду. Это позволит нам легче найти общее решение системы.

Для приведения матрицы к ступенчатому виду необходимо последовательно применять следующие операции:

1. Выбираем первый ненулевой элемент в первом столбце и делаем его равным единице, домножая соответствующую строку на обратное значение этого элемента. Этот элемент называется ведущим.
2. Обнуляем все остальные элементы в первом столбце, вычитая из каждой строки первую строку, домноженную на соответствующий элемент. Таким образом, второй столбец становится ступенчатым.
3. Повторяем описанные выше шаги для оставшихся столбцов, итерационно приводя матрицу к ступенчатому виду.

После выполнения этих операций матрица будет иметь ступенчатый вид и ее элементы будут приведены к минимальным дробям.

Приведение матрицы к ступенчатому виду позволяет нам использовать метод Гаусса или метод Гаусса-Жордана для дальнейшего решения системы линейных уравнений.

Важно отметить, что при приведении матрицы к ступенчатому виду необходимо следить за сохранением равенства системы уравнений. Это значит, что все проводимые операции нужно применять и к расширенной матрице системы, где последним столбцом являются свободные члены системы.

Полученный ступенчатый вид матрицы будет показывать зависимость переменных друг от друга и позволит найти общее решение системы линейных уравнений.

Шаг 3: Приведение матрицы к улучшенному ступенчатому виду

После получения ступенчатого вида матрицы в предыдущем шаге, мы можем перейти к приведению ее к улучшенному ступенчатому виду. Это позволяет нам получить дополнительную информацию о системе уравнений и найти общее решение.

1. Отметим ведущие элементы каждой строки. Ведущий элемент - это первый ненулевой элемент строки, и он должен быть равен 1. Если в строке нет ненулевых элементов, она считается нулевой.

2. Обнулим все элементы ниже ведущих элементов, чтобы на каждом шаге получить ступень в системе.

3. Для каждого нулевого столбца, в котором есть ненулевые элементы ниже, выберем строку с наибольшим ненулевым элементом и выполним элементарные преобразования строк, чтобы этот элемент стал ведущим для своей строки.

4. Повторим шаги 2 и 3 до тех пор, пока не достигнем улучшенного ступенчатого вида матрицы.

Приведение матрицы к улучшенному ступенчатому виду позволяет нам точно определить число свободных и зависимых переменных в системе уравнений. Это дает нам возможность найти общее решение системы и установить, существует ли одно решение, бесконечно много решений или система несовместна.

Если у вас возникли затруднения с приведением матрицы к улучшенному ступенчатому виду, стоит обратиться к методам Гаусса или Гаусса-Жордана. Эти методы также помогут вам получить улучшенный ступенчатый вид матрицы и найти общее решение системы линейных уравнений.

Шаг 4: Выписывание общего решения

После того, как мы нашли фундаментальную систему решений и базисное решение, мы можем перейти к выписыванию общего решения системы линейных уравнений.

Для этого мы используем найденные базисные решения и произвольные константы. Значения этих констант будут определяться условиями задачи или дополнительными уравнениями, если они имеются.

Общее решение системы линейных уравнений будет иметь вид:

x = c₁v₁ + c₂v₂ + ... + c_nv_n

Где c₁, c₂, ..., c_n - произвольные константы, а v₁, v₂, ..., v_n - найденные базисные решения.

Целью этого шага является представление общего решения системы линейных уравнений в форме, которая наиболее удобна для данной задачи или контекста. В некоторых случаях это может быть упрощение выражения до более простого вида или замена базисных решений другими эквивалентными векторами.

Пример нахождения общего решения

Рассмотрим следующую систему линейных уравнений:

Уравнение 1: 2x + 3y = 7

Уравнение 2: 4x - 2y = -2

Для начала решим данную систему методом Крамера:

1. Определитель основной системы:

D =

|2 3| = 2 * (-2) - 3 * 4 = -14

2. Определитель системы с заменой x:

Dx =

|7 3| = 7 * (-2) - 3 * (-1) = -11

3. Определитель системы с заменой y:

Dy =

|2 7| = 2 * (-1) - 7 * 4 = -30

Теперь можем найти значения переменных x и y:

4. Значение x:

x = Dx / D = -11 / -14 = 22 / 28 = 11 / 14

5. Значение y:

y = Dy / D = -30 / -14 = 60 / 28 = 30 / 14 = 15 / 7

Теперь найденные значения переменных можно подставить в исходные уравнения и проверить, являются ли они решением системы.

Пример системы линейных уравнений

Для наглядности рассмотрим пример системы линейных уравнений:

Система:

• Уравнение 1: 2x + 3y - z = 7
• Уравнение 2: 4x - 5y + 2z = 3
• Уравнение 3: 3x + y - 2z = 1

В данном примере у нас есть три уравнения с тремя неизвестными: x, y и z. Наша задача - найти их значения.

Чтобы найти решение системы линейных уравнений, мы можем воспользоваться методом Гаусса или методом Крамера. В данном случае будем использовать метод Гаусса.

Сначала приведем систему к треугольному виду путем элементарных преобразований:

• Уравнение 1: 2x + 3y - z = 7
• Уравнение 2: 4x - 5y + 2z = 3
• Уравнение 3: 3x + y - 2z = 1

Обнулим элементы под первым элементом:

• Уравнение 1: 2x + 3y - z = 7
• Уравнение 2 - 2 * Уравнение 1: -11y + 4z = -11
• Уравнение 3 - 1.5 * Уравнение 1: -0.5y + 1.5z = -8.5

Далее, обнулим элементы под вторым элементом:

• Уравнение 1: 2x + 3y - z = 7
• Уравнение 2: -11y + 4z = -11
• Уравнение 3 + 3.67 * Уравнение 2: 3.33z = -2.33

Теперь найдем значения неизвестных, начиная с последнего элемента:

• z = -2.33 / 3.33 = -0.7
• Уравнение 2: -11y + 4 * (-0.7) = -11 => -11y - 2.8 = -11 => -11y = -8.2 => y = 0.7455
• Уравнение 1: 2x + 3 * 0.7455 - (-0.7) = 7 => 2x + 2.2365 + 0.7 = 7 => 2x = 4.0635 => x = 2.03175

Таким образом, решение системы линейных уравнений равно:

• x = 2.03175
• y = 0.7455
• z = -0.7

Это общее решение системы, которое удовлетворяет всем уравнениям. Можно проверить подставив найденные значения в исходную систему и убедившись, что они действительно являются корректными решениями.

Шаги нахождения общего решения для данного примера

Для решения системы линейных уравнений и нахождения общего решения, следуйте следующим шагам:

1. Запишите систему линейных уравнений в матричной форме. Для данного примера это будет выглядеть так:

\[

\begin{align*}

2x + 3y + z & = 10 \\

-3x + 2y - z & = -4 \\

x - y + 3z & = 7 \\

\end{align*}

\]

2. Перепишите систему в расширенной матричной форме, добавив столбец свободных членов:

\[

\begin{bmatrix}

2 & 3 & 1 & 10 \\

-3 & 2 & -1 & -4 \\

1 & -1 & 3 & 7 \\

\end{bmatrix}

\]

3. Приведите расширенную матрицу к ступенчатому виду, используя элементарные преобразования строк:

\[

\begin{bmatrix}

1 & -1 & 3 & 7 \\

0 & -7 & 10 & 23 \\

0 & 0 & 5 & 5 \\

\end{bmatrix}

\]

4. Приведите матрицу к улучшенному ступенчатому виду, применяя обратные ходы Гаусса:

\[

\begin{bmatrix}

1 & 0 & 2 & 3 \\

0 & 1 & -2 & -2 \\

0 & 0 & 1 & 1 \\

\end{bmatrix}

\]

5. Запишите общее решение системы линейных уравнений, задав значения свободных переменных:

\[

\begin{align*}

x & = 3 - 2t \\

y & = -2 + 2t \\

z & = 1 \\

\end{align*}

\]

6. Представьте общее решение в векторной форме:

\[

\begin{bmatrix}

x \\

y \\

z \\

\end{bmatrix} =

\begin{bmatrix}

3 \\

-2 \\

1 \\

\end{bmatrix} +

t

\begin{bmatrix}

-2 \\

2 \\

0 \\

\end{bmatrix}, \quad t \in \mathbb{R}

\]

Таким образом, общее решение системы линейных уравнений данного примера будет представляться в виде указанного уравнения.