Интегралы являются одним из основных понятий математического анализа, широко применяемым в различных областях науки и инженерии. Одним из основных способов классификации интегралов является их разделение на сходящиеся и расходящиеся. В данной статье мы сосредоточимся на понятии сходящегося интеграла и рассмотрим, что именно означает его сходимость и как он работает.
Сходящийся интеграл является частным случаем интеграла и представляет собой предел значения интеграла при бесконечном увеличении своей области определения. Важно отметить, что сходящийся интеграл может быть непрерывным на всей своей области определения или только на отрезке, либо в некоторых точках. Это зависит от функции, которую мы интегрируем, и конкретных условий задачи.
Чтобы определить, является ли интеграл сходящимся, необходимо проанализировать поведение функции под интегралом при бесконечном увеличении своей области определения. Если значения функции стремятся к конечному пределу, то говорят, что интеграл сходится. В противном случае, интеграл расходится.
Например, рассмотрим интеграл от функции f(x) = 1/x в пределах от 1 до бесконечности. При бесконечном увеличении верхней границы интегрирования, значения функции будут стремиться к нулю. Поэтому, данный интеграл сходится.
Для вычисления значения сходящегося интеграла можно использовать различные методы, включая методы аналитического вычисления или численные методы, такие как метод Монте-Карло или метод трапеций. Выбор метода зависит от конкретной задачи и доступных вычислительных ресурсов.
Сходящиеся интегралы играют важную роль в различных областях математики, физики, экономики, статистики и других наук. Они позволяют решать широкий спектр задач, связанных с определением площадей, объемов, распределений вероятностей и многих других. Понимание сходимости интегралов является ключевым для более глубокого изучения анализа функций и их свойств.
Что такое сходящиеся интегралы
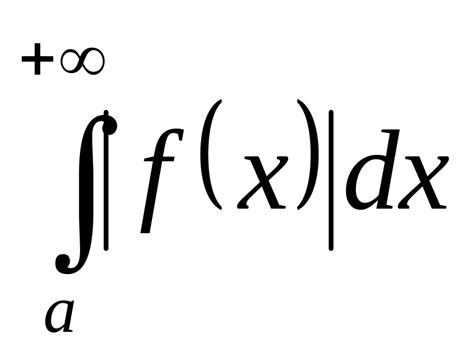
Сходящийся интеграл позволяет определить площадь под кривой или путь, пройденный объектом. Он также может использоваться при решении задач, связанных с определением массы, объема или центра масс.
Процесс вычисления сходящегося интеграла называется интегрированием. Он основан на разбиении интервала на маленькие части и замене каждой части суммой значений функции внутри этой части. Постепенно уменьшая размеры частей, мы можем получить точное значение интеграла.
Однако, сходящийся интеграл имеет границы рости. Чтобы определить, сойдется ли интеграл, необходимо проанализировать поведение функции на бесконечности или в точках неопределенности. Если функция удовлетворяет определенным условиям, интеграл сходится к конечному значению.
Есть разные типы сходящихся интегралов, таких как сходящиеся интегралы Римана или сходящиеся интегралы Лебега. Каждый тип имеет свои особенности и используется в различных областях математики и физики.
В заключение, сходящиеся интегралы играют важную роль в математике и науке, позволяя нам анализировать и вычислять различные величины и свойства функций. Понимание сходящихся интегралов является неотъемлемой частью математической грамотности и помогает развивать навыки аналитического мышления.
Определение и особенности
Основное отличие сходящегося интеграла от обычного интеграла состоит в том, что сходящийся интеграл имеет конечное значение, даже если функция, которую мы интегрируем, имеет бесконечное количество точек разрыва или является неограниченной в некоторых точках. В этом отличие от обычного интеграла, который не может быть вычислен для функций с бесконечными разрывами или неограниченной величиной.
Другой важной особенностью сходящегося интеграла является его свойство сходимости. Интеграл считается сходящимся, если его значение подходит к определенному числу при увеличении предела интегрирования. Если интеграл имеет конечное значение и при этом его значение со временем не меняется, то говорят, что интеграл сходится. Если же значения интеграла приближаются к некоторому пределу и при этом не имеют постоянного значения, то интеграл считается расходящимся.
Сходящиеся интегралы находят широкое применение в различных областях науки и техники, особенно в физике и инженерии. Это позволяет вычислять значения различных физических величин, таких как масса, объем, площадь, мощность и многие другие, используя интегральный метод вместо методов дискретизации или аппроксимации.
Сходимость и расходимость интегралов

В контексте сходящихся интегралов, сходимость означает, что интеграл имеет определенное, конечное значение. Это означает, что, при увеличении точности разбиения отрезка и уменьшения длины каждого подотрезка, интегральная сумма будет стремиться к фиксированному значению. Формально, интеграл сходится, если предел интегральной суммы приближается к определенному числу.
Сходимость интегралов связана с понятием непрерывности функции на заданном отрезке. Если функция достаточно гладкая и непрерывная, то интеграл обычно сходится. Однако существуют функции, для которых интеграл расходится, т.е. не имеет конечного значения.
Расходимость интеграла означает, что интегральная сумма не имеет определенного значения и не стремится к фиксированному числу при увеличении точности разбиения отрезка и уменьшении длины каждого подотрезка. Расходимость может быть вызвана различными факторами, например, функция может иметь бесконечные разрывы или особенности на заданном отрезке.
Расходимость интеграла означает, что интеграл не может быть вычислен стандартными методами и требует дополнительных усилий для его определения. В этом случае обычно используются специальные методы анализа, такие как ряды или интегралы с особыми точками.
Важно понимать, что расходимость интеграла не означает, что функция не является интегрируемой. Интегрируемость функции зависит от ее свойств, таких как ограниченность или непрерывность, и может быть установлена независимо от сходимости или расходимости интеграла.
Сходящиеся несобственные интегралы
Сходящийся несобственный интеграл представляет собой предел определенного интеграла, вычисленного на бесконечном промежутке или на промежутке, который содержит бесконечность в качестве одной или обеих границ. Он используется для вычисления площадей под графиком функции, которая не ограничена или не определена на всем заданном интервале.
Для того чтобы определить, является ли несобственный интеграл сходящимся или расходящимся, требуется вычислить его предел. Если предел существует и конечен, то интеграл называется сходящимся. Если предел не существует или бесконечен, то интеграл называется расходящимся.
Сходящиеся несобственные интегралы имеют важное применение в математике и физике. Они позволяют решать задачи, которые не могут быть решены с помощью обычных, собственных интегралов. Кроме того, сходящиеся несобственные интегралы играют роль в теории вероятности и статистике.
Для вычисления сходящихся несобственных интегралов используются различные методы, такие как замена переменной, интегрирование по частям и использование таблиц интегралов. Некоторые интегралы могут быть решены аналитически, в то время как для других может потребоваться численное интегрирование.
Важно отметить, что при вычислении сходящихся несобственных интегралов необходимо учитывать особые точки и разрывы функции на заданном промежутке. Это может потребовать разделения интеграла на несколько частей или использование теорем о сходимости несобственных интегралов.
Использование сходящихся несобственных интегралов позволяет решать широкий класс задач, связанных с определением площадей, вычислением центров масс, нахождением объемов и решением дифференциальных уравнений. Они также находят применение в физике для расчета массы, энергии и других физических величин.
Признаки сходимости

При изучении сходящихся интегралов очень важно уметь определить, сходится ли данный интеграл или нет. Для этого существуют различные признаки, которые позволяют сделать вывод о сходимости интеграла.
Одним из наиболее часто используемых признаков является признак сравнения. Он основан на сравнении исходной функции с более простой функцией, сходящейся или расходящейся. Если исходный интеграл можно сравнить с другим интегралом с уже известной сходимостью, то можно сделать вывод о сходимости или расходимости последнего.
Другим важным признаком сходимости интегралов является признак Дирихле. Он применяется для интегралов, в которых интегрируемая функция содержит произведение двух функций. Если одна из этих функций имеет ограниченную вариацию, а другая имеет ограниченное интеграл по ограниченному промежутку, то интеграл сходится.
Также существуют признаки Коши и Абеля. Признак Коши основан на сравнении интеграла с уже известной сходящейся или расходящейся числовой последовательностью. Если интеграл может быть уподоблен сходящейся последовательностью, то сходимость интеграла является абсолютной или условной. Признак Абеля применяется для определения сходимости интеграла с переменным пределом интегрирования или в случае, когда функция имеет особые точки.
Наконец, одним из основных признаков сходимости является признак сходимости Дирихле-Абеля. Он представляет собой усовершенствованный вариант признака Дирихле, который применяется для интегралов, содержащих синус или косинус в произведении. Он позволяет определить сходимость интеграла исходя из наличия основного периода функции.
| Признак | Условия | Сходимость | Расходимость |
|---|---|---|---|
| Признак сравнения | Если 0 ≤ f(x) ≤ g(x) на промежутке [a, +∞) | Если интеграл от g(x) сходится, то интеграл от f(x) также сходится | Если интеграл от g(x) расходится, то ничего о сходимости интеграла от f(x) сказать нельзя |
| Признак Дирихле | Если f(x) и g(x) непрерывны на промежутке [a, +∞) и f(x) имеет ограниченную вариацию, а g(x) имеет ограниченное интеграл по промежутку [a, x] | Интеграл от f(x) сходится | Интеграл от f(x) может как сходиться, так и расходиться |
| Признак Коши | Если для любого ε > 0 найдется такое x_0, что для всех x_1, x_2 > x_0 интеграл от f(x) по промежутку [x_1, x_2] не превосходит ε | Интеграл абсолютно сходится | Интеграл может как сходиться, так и расходиться |
| Признак Абеля | Если f(x) и g(x) непрерывны на промежутке [a, b] и F(x) и G(x) имеют пределы, когда x стремится к b | Интеграл от f(x) условно сходится | Интеграл от f(x) может как сходиться, так и расходиться |
| Признак сходимости Дирихле-Абеля | Если f(x) и g(x) непрерывны на промежутке [a, +∞), f(x) имеет периодически повторяющиеся основные интервалы, g(x) не меняет знак на промежутке [a, +∞) | Интеграл от f(x) сходится | Интеграл от f(x) может как сходиться, так и расходиться |








