Значение знака интеграла с кружком в математике и физике

Знак интеграла с кружком (∫) является одним из важных символов в математике и физике. Он представляет собой специальное обозначение для математической операции интегрирования. Интеграл используется для нахождения площадей под кривыми, вычисления суммы некоторых бесконечных рядов, а также для множества других приложений.

Когда интеграл применяется в математике, он описывает операцию, которая позволяет найти площадь криволинейной фигуры. Интеграл также может использоваться для нахождения объема тела или массы объекта. Он является одним из основных инструментов математического анализа и наряду с производной составляет его основу.

В физике интеграл применяется для описания различных физических процессов. Например, он используется для определения работы, совершенной над телом, нахождения центра масс системы, расчета энергии или определения силы тока через проводник. Знание интегралов позволяет физикам разрабатывать математические модели, описывающие физические явления и является неотъемлемой частью физических законов и формул.

Знак интеграла с кружком (∫) является одним из наиболее узнаваемых и важных символов в математике и физике. Он используется для нахождения площадей, объемов и выполнения различных вычислений. Знание и понимание интеграла с кружком играют ключевую роль в математическом анализе и физике, помогая ученым и инженерам понять основные законы и фундаментальные явления в нашем мире.

Объяснение интеграла

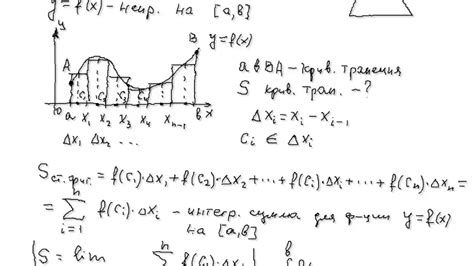
Итак, интеграл является обратной операцией к дифференцированию. Он позволяет найти не только производную функции, но и саму функцию, зная ее производную.

Геометрический смысл интеграла заключается в том, что он позволяет вычислять площади криволинейных фигур. Для этого область, внутри которой мы хотим найти площадь, разделяется на бесконечное количество маленьких элементов площади. Затем эти элементы складываются, и полученная сумма приближается к площади всей области.

Интеграл, помеченный кружком, называется интегралом Римана. Он является основным видом интеграла в математике и физике. Он записывается с помощью специальной формулы, которая включает в себя интегральное отображение, функцию и пределы интегрирования.

Определенный интеграл вычисляется по определенному промежутку. Он имеет численное значение и показывает величину той физической характеристики, которую мы исследуем.

Итак, интеграл – это мощный инструмент, который дает возможность решить множество задач в математике и физике, связанных с нахождением площадей, объемов и массы различных фигур и тел.

Интеграл как антипроизводная функции

Антипроизводная функция (интеграл) является общим решением дифференциального уравнения, то есть функцией, производная которой равна заданной функции. Интеграл часто обозначается знаком ∫ (знак интеграла), который похож на знак суммы, но имеет круглую форму "кружок".

Запись интеграла состоит из интегрального символа, функции под знаком интеграла (интегранда) и дифференциального элемента, указывающего независимую переменную. В общем случае запись интеграла выглядит так:

∫ f(x) dx

Здесь f(x) - интегрант, dx - дифференциальный элемент. Функция f(x), под знаком интеграла, определяет интеграл. Понятие интеграла возникает как непрерывное обобщение суммы Римана, позволяющее находить площади под графиками функций, длины кривых, массы тел и другие величины, связанные с данной функцией.

Интеграл может рассматриваться не только лишь в математике, но и в физике. Например, в физике он применяется для нахождения работы силы, перемещения по траектории и других величин, характеризующих физический процесс.

Интерпретация интеграла как площади под кривой

Знак интеграла с кружком в математике и физике имеет важную геометрическую интерпретацию. Он позволяет интерпретировать интеграл как площадь под кривой на графике функции.

Интеграл является удобным инструментом для вычисления площадей под кривыми различной формы. Простым примером может служить вычисление площади прямоугольника. Для этого используется интеграл от функции, которая равна ширине прямоугольника на каждом его отрезке:

∫ f(x) dx = S

Здесь f(x) - функция, которая выражает ширину прямоугольника на каждом его отрезке, а S - площадь прямоугольника.

Эта интерпретация интеграла распространяется на общий случай, когда кривая имеет сложную форму. Исходя из данной интерпретации, интеграл позволяет найти площадь фигуры, образованной кривой и осью абсцисс на графике функции.

Интеграл с кружком также позволяет определить направление интегрирования. Если знак интеграла направлен положительно, то это означает, что площадь вычисляется сверху-вниз (при условии, что ось абсцисс служит горизонтальной осью). Если же знак интеграла направлен отрицательно, то площадь вычисляется снизу-вверх.

Интерпретация интеграла как площади под кривой имеет широкие применения в различных областях науки и техники. Например, определение площади под графиком функции может быть полезным при решении задач, связанных с определением объема тела или вычислением работы, сделанной по силе во физике.

Использование интеграла в определении вероятности

Интеграл с кружком используется в математике для определения вероятности. Для этого применяется понятие плотности вероятности, которое позволяет вычислить вероятность события на основе функции плотности вероятности.

Функция плотности вероятности имеет следующий вид: f(x), где x – случайная переменная. Плотность вероятности показывает, насколько вероятно появление определенного значения случайной переменной в конкретной точке. Плотность вероятности также определяется как производная от функции распределения вероятностей.

Для вычисления вероятности события в заданном интервале используется интеграл от функции плотности вероятности. Интеграл с кружком позволяет вычислять площадь под графиком функции плотности вероятности в заданном интервале.

Формально вероятность события P(a \leq x \leq b) вычисляется с помощью интеграла по следующей формуле:

$P(a \leq x \leq b) = \int_a^b f(x) dx$

Где f(x) – функция плотности вероятности, a и b – границы интервала, а интеграл с кружком означает вычисление площади под графиком функции плотности вероятности в интервале от a до b.

Таким образом, интеграл с кружком является неотъемлемой частью определения вероятности в математике. Он позволяет вычислять вероятность событий на основе функции плотности вероятности и определенного интервала.

Применение интеграла для вычисления средних значений

Рассмотрим случай, когда функция f(x) задана на интервале [a, b]. Чтобы найти среднее значение функции на этом интервале, необходимо вычислить интеграл от функции f(x) на данном интервале, а затем поделить его на длину этого интервала (b-a).

Формально, среднее значение функции f на интервале [a, b] вычисляется по следующей формуле:

среднее значение = (1/(b-a)) * ∫_a^b f(x) dx

где ∫_a^b f(x) dx - интеграл от функции f(x) на интервале [a, b].

Таким образом, интеграл с кружком позволяет найти среднее значение функции на заданном интервале. Это может быть полезно, например, в физике, где средние значения могут представлять физические величины, такие как сила, плотность и т. д.

Связь между производной и интегралом

Производная функции показывает, как быстро меняется значение функции в зависимости от изменения аргумента. Она определяется как предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю. Процесс нахождения производной называется дифференцированием.

Интеграл функции, в свою очередь, позволяет найти площадь под графиком функции на заданном отрезке. Он является обратной операцией к дифференцированию и дает возможность восстановить функцию, зная ее производную. Интеграл также может быть использован для решения задач, связанных с нахождением общего решения дифференциальных уравнений.

Таким образом, производная и интеграл являются взаимно обратными операциями и играют важную роль в решении математических и физических задач. Они предоставляют нам возможность анализировать и понимать изменения функций и являются основой для дальнейшего изучения дифференциального исчисления и интегрального исчисления.

Производная	Интеграл
Определяет скорость изменения функции	Находит площадь под графиком функции
Дает информацию о направлении роста функции	Позволяет восстановить функцию по ее производной
Может быть использована для нахождения критических точек функции	Используется для решения задач с дифференциальными уравнениями

Понятие неопределенного интеграла

Неопределенный интеграл является обратной операцией к дифференцированию. Если f(x) – непрерывная функция, то её неопределенным интегралом называется функция F(x), производную которой можно получить дифференцированием: F'(x) = f(x). Таким образом, неопределенный интеграл позволяет восстановить исходную функцию по её производной.

Неопределенный интеграл не содержит верхнего и нижнего пределов интегрирования, поэтому называется неопределенным. Решая задачу нахождения неопределенного интеграла, получаем множество функций, которые отличаются друг от друга на константу C. Поэтому неопределенный интеграл также называют интегралом с постоянным слагаемым.

Неопределенный интеграл имеет множественное значение, которое может быть определено с точностью до константы. При нахождении неопределенного интеграла, обычно устанавливается условие F(0) = 0 для простоты вычислений. Также, при работе с неопределенными интегралами, важно помнить о правиле замены переменных, так как оно позволяет упростить интегрирование и сделать его более удобным.

Решение дифференциальных уравнений с помощью интегралов

Дифференциальные уравнения играют важную роль в математике и физике, так как позволяют описывать различные явления и процессы. Решение таких уравнений может быть сложной задачей, однако интегралы могут предложить эффективный способ их решения.

В общем виде дифференциальное уравнение может быть записано в виде:

dy/dx = f(x)

где y - неизвестная функция, x - независимая переменная, а f(x) - заданная функция, определяющая зависимость между производной исследуемой функции и переменной.

Для решения таких уравнений можно использовать методы интегрирования. Интегрирование позволяет найти функцию, производная которой равна заданной функции. Зная эту функцию, мы можем использовать ее для нахождения значения искомой функции y.

Для этого сначала находим неопределенный интеграл от заданной функции f(x):

∫f(x) dx

Определенный интеграл, который представляет собой площадь под графиком функции, может быть использован для нахождения конкретных значений функции y в определенных отрезках.

Использование интегралов для решения дифференциальных уравнений требует некоторых знаний и методик интегрирования. Это может включать применение различных формул интегрирования, методы замены переменных или интегрирования по частям. Также может понадобиться использование начальных условий для определения констант интегрирования.

Интегралы позволяют более глубоко изучать и понимать свойства исследуемой функции и ее производной, а также находить аналитические решения сложных дифференциальных уравнений. Дифференциальные уравнения с кружком, где знак интеграла указывает на это идентификацию производной с исходной функцией, позволяют использовать приемы интегрирования для получения аналитических решений.

Многомерные интегралы и их применение в физике

В физике многомерные интегралы широко применяются для описания различных явлений и законов природы. Например, многомерные интегралы используются при моделировании физических систем, расчете объемов и площадей, а также при решении уравнений в частных производных.

В механике многомерные интегралы играют важную роль при вычислении общего момента инерции тела, центра масс системы и других параметров, характеризующих движение и взаимодействие тел.

Также многомерные интегралы применяются при решении задач электродинамики, оптики и теплопроводности. Они позволяют описывать распределение электрического и магнитного поля, распространение света и тепла в пространстве.

Кроме того, многомерные интегралы используются в статистике и вероятностном анализе для описания случайных процессов и распределений вероятностей.

Таким образом, многомерные интегралы являются мощным инструментом для математического и физического моделирования, позволяющим описывать и анализировать сложные физические явления и процессы.

Интегралы Фурье и их роль в анализе сигналов

Основная идея интегралов Фурье состоит в разложении функции в ряд, состоящий из синусов и косинусов. Этот ряд называется рядом Фурье. Интегралы Фурье позволяют вычислить коэффициенты этого ряда и определить, какие гармонические компоненты присутствуют в исследуемом сигнале.

Разложение функции в ряд Фурье позволяет анализировать частотный спектр сигнала и определить его составляющие частоты и амплитуды. Это позволяет исследователям изучать различные свойства сигнала, такие как периодичность, частоты основных компонент, амплитуды и фазы. Этот анализ особенно полезен при обработке и сжатии аудио- и видеоданных, а также при решении задач распознавания образов.

Преобразование Фурье – это инструмент, позволяющий перейти от исходной функции к ее спектральной характеристике. Преобразование Фурье может применяться как для непрерывных сигналов, так и для дискретных значений, полученных в результате дискретизации аналогового сигнала.

С помощью интегралов Фурье можно анализировать широкий спектр сигналов, в том числе звуковые сигналы, электронные сигналы, оптические сигналы и др. Это делает их незаменимым инструментом в современных технологиях, таких как цифровая обработка сигналов и обработка изображений.

Кружок в знаке интеграла: значение и использование