Критические точки функции могут играть важную роль в анализе ее поведения и нахождении оптимальных значений. Но что именно означает понятие "критическая точка" и как ее определить?
Критическая точка функции - это точка, в которой ее производная или градиент равны нулю или не существуют. Такая точка может быть максимумом, минимумом или точкой перегиба. Определение критических точек позволяет нам понять, где функция достигает экстремальных значений и где происходят изменения ее поведения. Это важная информация для решения различных задач и оптимизации процессов.
Определение критических точек функции может быть достаточно простым процессом, если функция задана явно. Для этого необходимо найти ее производную и приравнять ее к нулю. После этого можно решить полученное уравнение и определить значения аргумента, при которых производная равна нулю. Эти значения и будут являться критическими точками функции. Однако, в некоторых случаях, определение критических точек может потребовать более сложных методов, таких как численное дифференцирование или использование численных методов оптимизации.
Важно отметить, что наличие критической точки не гарантирует наличие экстремума на функции. Для того чтобы определить, является ли точка максимумом или минимумом, необходимо проводить дополнительные исследования, такие как анализ второй производной или построение графика функции.
В заключение, понятие критической точки функции является важным инструментом для анализа ее поведения и оптимизации. Определение критических точек позволяет нам найти значения аргумента, при которых функция достигает экстремальных значений или происходит изменение ее поведения. Правильное определение критических точек может быть ключом к решению различных задач и приближению к оптимальным решениям.
Что такое критические точки?

Когда производная функции равна нулю в определенной точке, это может означать наличие локального минимума, максимума или точки перегиба. Локальный минимум представляет собой самую низкую точку функции в некоторой окрестности, а локальный максимум – самую высокую. Точка перегиба отмечает изменение направления кривой, где функция может менять свой рост с положительного на отрицательный или наоборот.
Критические точки могут также указывать на точки разрыва функции, когда функция не определена или имеет несогласованное поведение. Это может происходить при делении на ноль, при использовании логарифма или при корне отрицательного числа.
Определение критических точек функции позволяет нам анализировать ее поведение, находить экстремумы и точки разрыва. Это полезный инструмент в изучении функций и их графиков в математике и физике.
Значение критических точек в анализе функций
Знание критических точек позволяет определить, где функция достигает экстремумов (минимумов или максимумов) и где она меняет свое поведение. На основе этих точек можно построить график функции и выявить особенности ее поведения.
Если производная функции в критической точке равна нулю, то эта точка называется стационарной. Однако стационарная точка может быть как точкой экстремума, так и точкой перегиба функции. Чтобы определить, какая именно точка является стационарной, необходимо анализировать окрестность данной точки с помощью второй производной функции.
Если в критической точке функции производная не существует, то такая точка может быть точкой перегиба или разрыва функции. Наличие разрыва в функции может указывать на наличие особых участков или различных ветвей функции.
Изучение критических точек помогает понять общую форму графика функции, определить области возрастания и убывания, а также наличие экстремумов и других особых точек. Эта информация важна для ряда прикладных задач, таких как оптимизация, нахождение максимумов и минимумов функции, а также прогнозирование поведения системы.
Как определить критические точки?
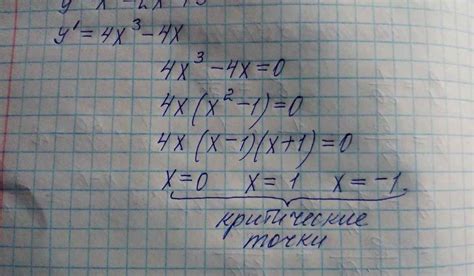
Для определения критических точек функции необходимо выполнить следующие шаги:
- Найдите первую производную функции.
- Приравняйте производную к нулю и решите уравнение для нахождения критических точек.
- Исследуйте значения производной вокруг найденных точек.
- Если производная меняет знак с плюса на минус, то в данной точке функция имеет локальный максимум.
- Если производная меняет знак с минуса на плюс, то в данной точке функция имеет локальный минимум.
- Если производная не меняет знак, то данная точка может быть либо точкой перегиба, либо экстремумом.
- Проверьте значения функции в найденных точках, чтобы окончательно определить тип критической точки.
Важно помнить, что наличие критических точек не гарантирует, что функция имеет в них экстремумы или точки перегиба. Для окончательного анализа функции нужно исследовать и другие характеристики, такие как вторая производная или поведение функции на бесконечностях.
Исключение значений
В некоторых случаях функция может иметь значения, которые невозможно вычислить или точно определить. Эти значения называются исключениями. Исключения могут возникать, например, при делении на ноль или при использовании некорректных аргументов функции.
Критические точки функции могут быть связаны с исключительными значениями. На этих точках функция может иметь разрывы, особые точки или не быть определенной вовсе. Важно учитывать исключения, поскольку они могут повлиять на корректность работы функции и результаты вычислений.
Определение исключительных значений и их обработка являются важными аспектами программирования и математического анализа. Возможные подходы включают проверку аргументов функции на корректность, использование условных операторов для избежания делений на ноль и другие операции, которые могут привести к исключениям, а также использование специальных обработчиков исключений для предотвращения сбоев программы.








