В математике дифференцируемость функции является одним из ключевых понятий. Она означает, что функция может быть представлена производной, то есть имеет определенный наклон в каждой точке своей области определения.
Однако существуют функции, которые не являются дифференцируемыми в некоторых точках или на всей своей области определения. Это может быть вызвано различными причинами, такими как наличие разрывов в функции или особенностей в ее поведении, например, в точках излома или вершине ветви.
Недифференцируемость функции влечет за собой ряд последствий. Во-первых, это означает, что в этих точках функция не имеет производной, а следовательно, не может быть использована для аппроксимации, оптимизации или других задач, связанных с производными. Во-вторых, в таких точках функция может иметь различные свойства, которые не характерны для дифференцируемых функций, например, может быть неограниченно возрастающей или убывающей.
Примеры функций, не дифференцируемых в некоторых точках:
- Модульная функция (|x|) имеет разрыв в точке 0, поэтому не дифференцируема в нуле.
- Функция Хэвисайда (H(x)) не имеет производной в точке 0, так как значение производной в этой точке равно бесконечности.
- Функция Дирихле (D(x)) не имеет производной в ни одной точке, так как она осциллирует между значениями 0 и 1.
Изучение функций, не дифференцируемых в некоторых точках, позволяет лучше понять их особенности и свойства. Также это является важным аспектом при решении прикладных задач, где требуется анализ функций и их поведения.
Причины недифференцируемости функций
- Угловые точки: Некоторые функции имеют точки, в которых они имеют касательную линию, но не имеют касательной. Эти точки называются угловыми точками. В таких точках функция не является дифференцируемой.
- Разрывы: Функции могут иметь точки, в которых они не определены или имеют разрывы. В этих точках функция непрерывна и не имеет касательной линии, что делает ее недифференцируемой.
- Иррациональность: Многие иррациональные функции не дифференцируемы в своих точках. Например, функция синуса имеет несколько точек, в которых она не является дифференцируемой.
- Несходимость: Функции могут быть не сходящимися в определенных точках, что делает их недифференцируемыми в этих точках.
- Скачки: Некоторые функции могут иметь точки, в которых они имеют скачок или осцилляции. В этих точках функция не имеет касательной линии и, следовательно, не является дифференцируемой.
Несуществование производной
Причины несуществования производной могут быть различными. Например, если функция имеет разрыв или разрыв первого рода в определенной точке, то производная в этой точке не будет существовать. Также, если функция имеет угловую точку или вертикальную асимптоту, то производная не будет определена в этих точках.
Несуществование производной накладывает ограничения на поведение функции в точке или на интервале. В таких точках функция может быть разрывной, иметь особые значения или угловые точки. Это может отражаться на поведении функции в окрестности несуществующей производной и влиять на ее свойства и график.
Несуществование производной имеет важные практические последствия. К примеру, в задачах оптимизации, где требуется найти экстремум функции, наличие разрывов или угловых точек может затруднить или сделать невозможным решение задачи. Также, в теории вероятностей и математической статистике, необходимо учитывать разрывы функций и искать альтернативные подходы для решения задач.
Итак, несуществование производной является одной из основных причин, по которой функция может быть не дифференцируема. Это свидетельствует о нарушении гладкости и непрерывности функции в определенных точках или интервалах, и может иметь существенное влияние на ее свойства и поведение.
Разрывы и разрывные точки функции
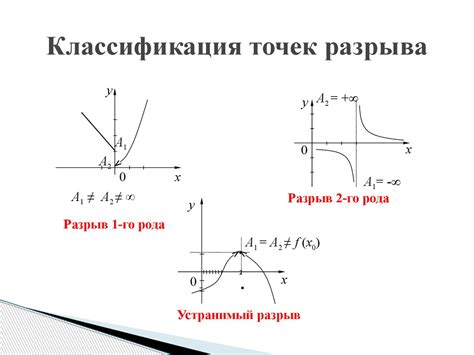
Изолированный разрыв может возникнуть, например, когда функция имеет различные пределы в двух сторонах одной точки. Асимптотический разрыв возникает, когда функция приближается к бесконечности или к некоторой константе в пределах определенной области. Разрывная точка на границе области определения функции происходит, если функция не имеет предела в этой точке.
Разрывы и разрывные точки могут иметь различные последствия. Например, функция может не быть дифференцируемой в точке разрыва или в окрестности разрывной точки. Это означает, что график функции имеет угловые точки или вертикальные асимптоты, что является результатом различий в значениях функции.
Разрывы также могут привести к тому, что функция не удовлетворяет условию Липшица, что влияет на ее сходимость и существование решений уравнений, содержащих эту функцию. Кроме того, разрывы могут иметь влияние на интегралы функции, что может привести к изменению значения интеграла или его несуществованию.
Несобственная точка нормализации
Одна из основных причин возникновения несобственной точки нормализации - разрывность функции. Может быть, функция имеет точку, в которой не определена или имеет разные значения на разных сторонах этой точки. Несобственная точка нормализации возникает тогда, когда такой разрыв является гладким, то есть все производные функции существуют до этой точки.
Еще одна причина возникновения несобственной точки нормализации - функция, значения которой стремятся к бесконечности. Например, если функция имеет вертикальную асимптоту или имеет полюс.
Несобственная точка нормализации имеет важные последствия для анализа функции. Она является исключительной точкой, где можно потерять непрерывность и, соответственно, дифференцируемость функции. При анализе функции вблизи такой точки необходимо использовать альтернативные методы, такие как разложение в ряд или применение теорем Гаусса-Остроградского или Стокса.
Вывод: несобственная точка нормализации является особой точкой в функции, которая не является непрерывной, но при этом все ее производные существуют. Она может возникнуть из-за разрыва в определении функции или при стремлении значений функции к бесконечности. Несобственная точка нормализации имеет важные последствия для анализа функции и требует применения дополнительных методов анализа.
Неустранимые особенности функции

Некоторые функции могут обладать неустранимыми особенностями, которые делают их не дифференцируемыми. Это может происходить по разным причинам:
| 1. | Разрывы в определении функции. Если функция имеет разрыв в определении, например, разрыв в точке или интервале, то она не будет дифференцируемой в этих точках или интервалах. Например, функция модуля |x| имеет разрыв при x = 0, поэтому она не является дифференцируемой в этой точке. |
| 2. | Точки локального минимума или максимума. Если функция имеет локальный минимум или максимум в точке, то она не будет дифференцируемой в этой точке. Например, функция f(x) = |x| имеет локальный минимум в x = 0, поэтому она не дифференцируема в этой точке. |
| 3. | Острые или угловые точки. Если функция имеет острый или угловой перегиб в точке, то она не будет дифференцируемой в этой точке. Например, функция f(x) = √x имеет острый перегиб при x = 0, поэтому она не дифференцируема в этой точке. |
Эти неустранимые особенности функции могут иметь различные последствия. Например, они могут приводить к несуществованию производной в некоторых точках или интервалах, ограничивать область определения функции и изменять поведение функции вблизи этих особых точек.
Непрерывные функции, но не дифференцируемые
Наиболее распространенным примером такой функции является модульная функция, которая определена как:
| Функция | Определение |
|---|---|
| |x| | { x, при x >= 0 -x, при x < 0} |
Эта функция непрерывна на всей числовой оси, но не дифференцируема в точке x = 0. В этой точке у нее скачок значений, что препятствует определению ее производной.
К другим примерам функций, которые могут быть непрерывными, но не дифференцируемыми, относятся:
- Функция Хеависайда, которая принимает значение 0 при x < 0 и 1 при x >= 0
- Функция Дирихле, которая равна 1, если x – рациональное число, и 0, если x – иррациональное число
Все эти функции имеют общую особенность – возникновение разрывов или скачков значений, что препятствует их дифференцируемости в некоторых точках. Это может иметь значительное значение в математическом и физическом моделировании, где необходимо учитывать такие разрывы или скачки значений.








