Подбор корня уравнения - это одна из основных задач математического анализа, которая имеет широкое применение в различных областях науки и техники. Он позволяет найти приближенное значение корня уравнения, когда аналитическое решение неизвестно или трудно получить.
Основные принципы подбора корня уравнения основаны на использовании итерационных методов и приближенных формул. Одним из таких методов является метод Ньютона-Рафсона, который основан на использовании линейной аппроксимации функции в окрестности корня уравнения.
Метод Ньютона-Рафсона является одним из наиболее эффективных методов подбора корня уравнения благодаря своей сходимости и скорости вычислений. Он является основой для множества других методов, таких как метод хорд, метод секущих и метод простой итерации.
Важно отметить, что подбор корня уравнения требует предварительного выбора начального приближения, которое может значительно влиять на точность и скорость сходимости метода. Поэтому выбор начального приближения является важной задачей и может осуществляться различными способами, например, с использованием графического или аналитического подхода.
В заключение, подбор корня уравнения является важной задачей математического анализа, которая имеет большое практическое применение. Он позволяет решать различные задачи, связанные с нахождением приближенного значения корня уравнения, и основывается на принципах итерационных методов и аппроксимации функций.
Важность корня уравнения

Знание корня уравнения имеет большое значение во многих областях, таких как физика, экономика, инженерия и другие. Оно позволяет решать различные проблемы, находить оптимальные значения и предсказывать результаты.
Методы поиска корня уравнения имеют большое практическое применение. Существуют различные аналитические и численные методы, которые позволяют найти корень уравнения. К ним относятся такие методы, как метод половинного деления, метод Ньютона-Рафсона, метод простой итерации и другие.
Умение находить корень уравнения помогает в решении сложных задач, оптимизации и моделировании различных процессов. Использование правильного метода поиска корня уравнения позволяет получить точные и надежные результаты.
Таким образом, понимание и использование корня уравнения является важным навыком для математиков, исследователей и практиков в различных областях науки и техники.
Основные принципы выбора корня уравнения
При решении уравнений одной переменной необходимо выбрать корень, который будет удовлетворять условиям задачи и давать наиболее подходящий результат. При выборе корня уравнения следует придерживаться следующих основных принципов:
1. Подбор корня путем применения методов и алгоритмов:
Выбор корня уравнения может происходить с применением различных методов и алгоритмов, таких как методы итераций, метод половинного деления, метод Ньютона и другие. Наиболее подходящий метод выбирается исходя из типа уравнения и его свойств.
2. Анализ свойств уравнения:
Перед выбором корня уравнения важно проанализировать его свойства. Например, если уравнение имеет рациональные коэффициенты, то наиболее подходящим корнем может быть рациональное число. Если уравнение имеет корень с помощью квадратного корня, то следует выбрать такой корень, чтобы избежать мнимых чисел.
3. Учет граничных условий:
При выборе корня уравнения необходимо учесть граничные условия. Например, если уравнение описывает физический процесс, то выбранный корень должен удовлетворять физическим ограничениям и быть в пределах разумных значений.
4. Проверка результатов:
После выбора корня уравнения необходимо проверить результаты подстановкой найденного значения в исходное уравнение. Если подстановка является верной и уравнение удовлетворяет условиям задачи, то выбранный корень считается правильным.
Следуя этим основным принципам, можно выбрать наиболее подходящий корень уравнения, что позволит получить правильный и точный результат решения задачи.
Методы подбора корня уравнения

В зависимости от типа уравнения применяются различные методы подбора корня:
| Тип уравнения | Метод подбора корня |
|---|---|
| Линейное уравнение | Метод замены переменной |
| Квадратное уравнение | Метод дискриминанта |
| Нелинейное уравнение | Метод бисекции |
Метод замены переменной заключается в замене искомой переменной на новую, для которой имеется явное выражение для значения в зависимости от известных величин. Применяется в случае линейного уравнения.
Метод дискриминанта используется для решения квадратного уравнения. Он основан на вычислении дискриминанта и последующем подборе корней в зависимости от его значения.
Метод бисекции применяется для решения нелинейных уравнений. Он основан на принципе деления отрезка пополам и последовательном подборе значений для определения корня.
Основная цель метода подбора корня уравнения состоит в нахождении значений переменных, при которых уравнение принимает заданное значение. Этот процесс требует тщательной работы с уравнением и применения соответствующих методов подбора корня.
Как выбрать начальное приближение корня уравнения
Существует несколько способов выбора начального приближения:
- Графический метод: Используя график функции, можно примерно определить положение корня. Начальное приближение можно взять в окрестности этой точки.
- Итерационный метод: Значение корня можно приближенно найти с помощью предыдущих итераций. Начальное приближение может быть равно значению предыдущего приближения либо какой-либо другой известной точке в окрестности корня.
- Аналитический метод: В некоторых случаях, основываясь на свойствах функции, можно аналитически найти начальное приближение. Например, если функция монотонна, можно взять начальное приближение как значение функции при некотором известном аргументе.
Необходимо учитывать, что выбор начального приближения корня может влиять на сходимость метода и точность результата. На практике рекомендуется проверять несколько начальных приближений и анализировать полученные результаты для выбора наиболее оптимального.
Метод половинного деления в подборе корня уравнения
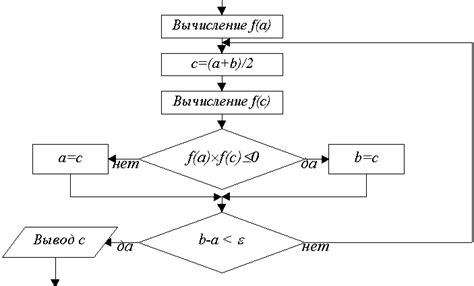
Данный метод подразумевает разбиение интервала, содержащего корень уравнения, на две равные части. Если значения функции на концах интервала имеют разные знаки, то корень уравнения гарантированно находится внутри этого интервала. Затем процесс деления интервала на две равные части повторяется до тех пор, пока не будет достигнута заданная точность.
Алгоритм метода половинного деления можно представить в виде следующей таблицы:
| Шаг | Левая граница интервала | Правая граница интервала | Значение функции в середине интервала |
|---|---|---|---|
| 1 | $a_1$ | $b_1$ | $f\left(\frac{a_1 + b_1}{2} ight)$ |
| 2 | $a_2$ | $b_2$ | $f\left(\frac{a_2 + b_2}{2} ight)$ |
| ... | ... | ... | ... |
| n | $a_n$ | $b_n$ | $f\left(\frac{a_n + b_n}{2} ight)$ |
В таблице указаны все значения границ интервала и значения функции в середине интервала на каждом шаге алгоритма. Уточнение корня уравнения происходит путем выбора нового интервала, состоящего из границ с тем знаком функции, которые имели значения разного знака.
Преимуществом метода половинного деления является его простота и надежность, при условии соблюдения определенных условий (непрерывность функции, наличие только одного корня на интервале и т.д.). Однако данный метод обычно является менее эффективным по сравнению с более сложными численными методами.
Метод простой итерации для нахождения корня уравнения
Для применения метода простой итерации необходимо иметь уравнение в виде f(x) = 0, где f(x) – функция, корнем которой является x. Далее, уравнение приводится к эквивалентному виду x = g(x), где g(x) – некоторая функция, называемая итерационной.
Алгоритм метода простой итерации выглядит следующим образом:
- Выбрать начальное приближение x₀ для корня уравнения.
- Вычислить новое приближение x₁ с помощью итерационной формулы x₁ = g(x₀).
- Повторять шаг 2 до достижения заданной точности (например, до тех пор, пока |xₙ - xₙ₋₁| > ε, где ε – заданная точность).
- Получить найденное приближенное значение корня x̂.
Успешность применения метода простой итерации зависит от выбора итерационной функции g(x) и начального приближения x₀. Итерационная функция должна быть такой, чтобы последовательность x₀, x₁, x₂, ... сходилась к искомому корню. Также важно выбрать начальное приближение близким к корню уравнения.
Метод простой итерации широко применяется для решения уравнений, особенно в случае, когда нет аналитического способа нахождения корня. Важным преимуществом метода является его простота и универсальность. Но следует заметить, что метод простой итерации может быть неэффективен в некоторых случаях, если итерационная функция выбрана неправильно или начальное приближение далеко от корня уравнения.
Метод Ньютона-Рафсона в поиске корня уравнения

Применение метода Ньютона-Рафсона осуществляется в несколько итераций, начиная с некоторого начального приближения корня уравнения. На каждой итерации находится точка пересечения касательной прямой с осью абсцисс, которая и становится новым приближением корня. Этот процесс продолжается до достижения определенной точности или заданного числа итераций.
Основным преимуществом метода Ньютона-Рафсона является его быстрота сходимости. Если начальное приближение корня достаточно близко к истинному значению, то метод сходится очень быстро. Однако, если начальное приближение далеко от корня, метод может не сойтись вообще или сходиться медленно.
Для применения метода Ньютона-Рафсона необходимо знать производную функции, корень которой ищется. Если производная в точке, близкой к истинному значению корня, равна нулю или близка к нулю, метод может сходиться медленно или вовсе не сходиться.
Как правило, метод Ньютона-Рафсона используется для решения нелинейных уравнений, когда другие методы (например, метод деления пополам) сходятся медленно или не подходят вовсе. Также данный метод широко применяется в задачах оптимизации, как один из составляющих алгоритмов численного нахождения экстремума функции.
| Преимущества метода Ньютона-Рафсона | Недостатки метода Ньютона-Рафсона |
|---|---|
| + Быстрая сходимость при хорошем начальном приближении | - Возможна медленная или отсутствующая сходимость при плохом начальном приближении |
| + Применим для нелинейных уравнений | - Требуется знание производной функции |
| + Широкое использование в задачах оптимизации | - Возможны особые случаи с низкой производной |
Сравнение и выбор наиболее эффективного метода при подборе корня уравнения
Один из наиболее простых и распространенных методов – метод деления отрезка пополам. Он заключается в разбиении интервала [a, b] пополам и проверке, в какой половине интервала находится корень. Этот метод прост в реализации, но требует большого числа итераций, особенно для уравнений с незначительными изменениями функции.
Более эффективным методом является метод Ньютона. Он основывается на итерационном алгоритме и требует меньшего количества итераций для достижения точности. Однако, метод Ньютона требует знания производной функции, что может быть затруднительно в некоторых случаях.
Еще одним эффективным методом является метод секущих. Он также использует итерационный алгоритм, но не требует знания производной функции. Вместо этого, метод секущих использует наклон прямой, проходящей через две точки. Этот метод обычно требует большего числа итераций, но может быть более универсальным для различных видов функций.
Выбор наиболее эффективного метода зависит от конкретной задачи и требуемой точности. Если функция имеет простой вид и производная легко вычисляется, метод Ньютона может быть наиболее эффективным. Если производную сложно или невозможно вычислить, метод секущих может быть предпочтительнее. Если точность не играет большой роли, то метод деления отрезка пополам может быть достаточно эффективным.








