Решение системы уравнений является важной задачей в математике и науке. Когда мы сталкиваемся с системой уравнений, нам необходимо определить, существует ли решение или его нет. Ответ на этот вопрос зависит от свойств системы уравнений и ее компонентов.
Существует несколько методов, которые мы можем использовать для определения существования решения системы уравнений. Один из таких методов - метод Гаусса-Жордана. Он заключается в преобразовании исходной системы уравнений таким образом, чтобы мы могли сделать вывод о существовании или отсутствии ее решения.
Кроме того, мы можем использовать теорему Кронекера-Капелли для определения существования решения системы уравнений. Согласно этой теореме, система уравнений имеет решение, если и только если ранг матрицы системы равен рангу расширенной матрицы.
Таким образом, определение существования решения системы уравнений является важным шагом в процессе ее решения. Наличие или отсутствие решений зависит от характеристик системы уравнений и может быть определено с помощью различных методов и теорем.
Что такое система уравнений?

Существует два типа систем уравнений: линейные и нелинейные. Линейные системы состоят из линейных уравнений, в которых все неизвестные входят с степенью 1. Нелинейные системы могут состоять из уравнений с различными степенями.
Решение системы уравнений может быть уникальным или неограниченным. Уникальное решение означает, что существует только один набор значений неизвестных, который удовлетворяет всем уравнениям системы. Неограниченное решение означает, что существует бесконечно много наборов значений, удовлетворяющих системе уравнений.
В случае, когда система уравнений не имеет решения, говорят, что система несовместна. Это означает, что невозможно найти набор значений неизвестных, удовлетворяющий всем уравнениям системы.
Решение системы уравнений может быть найдено различными методами, такими как метод подстановки, метод исключения и матричные методы. Выбор метода зависит от структуры системы и личных предпочтений решателя.
Чем отличается система уравнений от уравнения?
Система уравнений – это несколько уравнений, которые связаны между собой и имеют общие переменные. Решением системы уравнений являются значения переменных, при которых все уравнения системы выполняются одновременно.
Основное отличие системы уравнений от уравнения в том, что в системе может быть несколько переменных и несколько уравнений, которые должны выполняться одновременно, чтобы найти значения переменных, при которых система имеет решение. В случае уравнения может быть только одна переменная и одно уравнение.
Для решения системы уравнений применяют методы алгебраического описания, такие как метод подстановки, метод сложения или вычитания уравнений, метод определителей и другие.
| Уравнение | Система уравнений |
|---|---|
| Одна переменная | Несколько переменных |
| Одно уравнение | Несколько уравнений |
| Один корень | Несколько решений |
Как определить, имеет ли система уравнений решение?

Для определения, имеет ли система уравнений решение, необходимо провести соответствующий анализ. Существует несколько методов, которые позволяют определить наличие или отсутствие решения системы уравнений.
1. Метод подстановки: для каждого уравнения системы выполняем подстановку найденных значений переменных во все уравнения и проверяем, выполняются ли они. Если все уравнения выполняются, то система имеет решение.
2. Метод сложения/вычитания: складываем (или вычитаем) уравнения друг с другом так, чтобы одна из переменных уничтожилась. Если после упрощения полученного уравнения остается только одна переменная, то система имеет решение.
3. Метод определителей: составляем расширенную матрицу системы уравнений и находим значение её определителя. Если определитель равен нулю, то система не имеет решения, иначе система имеет решение.
4. Метод Гаусса: приводим систему к ступенчатому виду с помощью элементарных преобразований. Если в ступенчатой матрице есть строка, у которой все элементы равны нулю, но свободный член не равен нулю, то система не имеет решения. В противном случае, система имеет решение.
5. Метод Крамера: решаем систему методом Крамера, вычисляя значения переменных с помощью отношения определителей. Если все определители, включая определитель системы, отличны от нуля, то система имеет решение.
Использование этих методов позволяет определить, имеет ли система уравнений решение, и найти его, если оно существует.
Достаточные условия решения системы уравнений
Однако, существуют случаи, когда система уравнений может иметь бесконечное количество решений. Это происходит, когда уравнения могут быть выражены одно через другое или когда в систему добавляется свободная переменная.
Другими достаточными условиями решения системы уравнений являются совместность и совместимость системы. Совместность означает, что система имеет хотя бы одно решение, тогда как совместимость означает наличие хотя бы одного набора значений переменных, удовлетворяющих всем уравнениям системы.
Важно отметить, что есть случаи, когда система уравнений не имеет решений. Такая система называется несовместной. Несовместность может быть вызвана противоречивыми условиями в уравнениях или недостаточным количеством уравнений для определения значений всех переменных.
| Система уравнений | Достаточное условие решения | Пример |
| 2x + 3y = 8 | 2 уравнения, 2 неизвестных | 2x + 3y = 8 |
| 3x - 2y = 4 | Совместность, совместное решение | 3x - 2y = 4 |
| 5x + 2y = 10 | Бесконечное количество решений | 5x + 2y = 10 |
| 4x + 2y = 8 | Несовместность | 4x + 2y = 8 |
Понимание этих достаточных условий решения системы уравнений позволяет более эффективно и точно решать математические задачи, связанные с системами уравнений.
Как проверить является ли система уравнений совместной или несовместной?

Система уравнений называется совместной, если существует хотя бы одно решение, удовлетворяющее всем уравнениям этой системы. Для определения существования решения используются методы решения систем, такие как метод подстановки, метод равных коэффициентов, метод Гаусса и другие.
Система уравнений называется несовместной, если не существует ни одного решения, удовлетворяющего всем уравнениям системы. Это может быть вызвано противоречивыми условиями или неправильным построением задачи. Если при решении системы получается противоречие, например, 0 = 1, то система уравнений является несовместной.
Пример:
Рассмотрим систему уравнений:
x + 2y = 3
2x - 4y = 1
Составим матрицу коэффициентов и приведем ее к ступенчатому виду:
| 1 2 | 3
| 2 -4 | 1
Путем элементарных преобразований получим следующую матрицу:
| 1 2 | 3
| 0 -8 | -5
В данном случае полученная матрица не имеет противоречивых строк, поэтому система уравнений является совместной. Также можно заметить, что система имеет единственное решение: x = 1, y = -1/2.
Итак, для определения является ли система уравнений совместной или несовместной, необходимо решить систему с использованием соответствующих методов решения уравнений и проанализировать полученные результаты.
Методы решения систем уравнений
Метод подстановки
Метод подстановки является одним из самых простых методов решения системы уравнений. Он заключается в том, чтобы выразить одну переменную через другую в одном из уравнений и подставить это выражение в другое уравнение. Проделав подобные преобразования для всех переменных, получаем значения каждой переменной.
Метод сложения/вычитания
Метод сложения/вычитания, также известный как метод комбинирования или метод метода Гаусса, заключается в том, чтобы сложить/вычесть уравнения таким образом, чтобы одна переменная уничтожилась. Затем проделываем аналогичные преобразования для других переменных. В результате получаем значения переменных.
Метод определителей
Метод определителей основан на решении системы уравнений через нахождение определителя матрицы коэффициентов системы. Если определитель не равен нулю, то система имеет единственное решение. Если определитель равен нулю, то система может иметь бесконечное количество решений или не иметь их вовсе.
Метод Гаусса
Метод Гаусса, также известный как метод исключения Гаусса, является одним из наиболее эффективных способов решения системы уравнений. Он заключается в приведении расширенной матрицы системы к ступенчатому виду путем элементарных преобразований строк. Затем выполняют обратные ходы и последовательно находят значения переменных.
Метод Крамера
Метод Крамера основан на использовании определителей для вычисления значений переменных. Здесь каждая переменная выражается через определитель, который вычисляется на основе матрицы коэффициентов системы. Метод Крамера применим только к системам, у которых число уравнений совпадает с числом неизвестных и определитель матрицы коэффициентов не равен нулю.
Выбор метода решения системы уравнений зависит от сложности системы и требуемой точности результата. Каждый метод имеет свои преимущества и недостатки, а оптимальный выбор зависит от конкретной ситуации.
Как решить систему линейных уравнений?
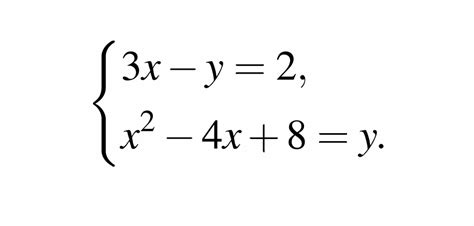
Для решения системы линейных уравнений необходимо следовать определенному алгоритму.
1. Запишите систему уравнений. Система может содержать одно или несколько уравнений с неизвестными переменными.
2. Преобразуйте систему уравнений таким образом, чтобы все уравнения имели одинаковое количество неизвестных.
3. Примените метод гаусса или метод Крамера для нахождения решения системы уравнений. В случае метода гаусса, необходимо последовательно выполнять элементарные преобразования строк матрицы коэффициентов, чтобы получить треугольную матрицу. Затем решите получившуюся систему снизу вверх. В случае метода Крамера, найдите определители матриц, заменив столбец коэффициентов на столбец свободных членов и решив систему определителей по правилу Крамера.
4. Проверьте решение найденной системы, подставив полученные значения переменных во все уравнения системы. Если все уравнения выполняются, то полученные значения являются решением системы уравнений.
5. Если система не имеет решений или имеет бесконечное количество решений, это также можно определить при решении. В таких случаях, возможно, требуется провести дополнительные действия для выяснения природы системы уравнений.
Таким образом, следуя этим шагам, можно решить систему линейных уравнений и найти значения неизвестных переменных.
Метод Гаусса: основные шаги
Основные шаги метода Гаусса:
1. Прямой ход
В данном шаге матрица расширенной системы приводится к ступенчатому виду. Для этого выполняются следующие элементарные преобразования строк:
- Расположение уравнений таким образом, чтобы ведущий элемент (первый ненулевой элемент) каждого уравнения был наибольшим среди остальных в его столбце.
- Деление каждого уравнения на его ведущий элемент, чтобы привести его к виду, где ведущий элемент равен единице.
- Вычитание первого уравнения, умноженного на константу, из всех остальных уравнений, чтобы обнулить все элементы под ведущим элементом.
2. Обратный ход
После приведения матрицы к ступенчатому виду, выполняется обратный ход для нахождения значений неизвестных. В этом шаге начинают с последнего уравнения и, работая сверху вниз, используют найденные значения неизвестных для вычисления остальных.
Если в результате обратного хода получается противоречие (например, ноль, отличный от нуля), то система уравнений не имеет решений. Если в результате обратного хода получается свободная переменная (переменная, которую можно выбрать любым значением), то система имеет бесконечное количество решений. Иначе, если все переменные определены, то система имеет единственное решение.
Метод Крамера: условия и примеры
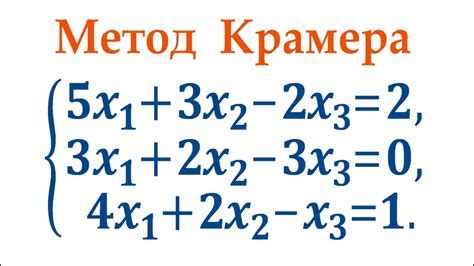
Условия применимости метода Крамера:
- Система уравнений должна быть однородной, то есть правая часть каждого уравнения должна быть нулевой.
- Определитель основной матрицы системы должен быть ненулевым.
- Количество уравнений должно быть равно количеству неизвестных.
Применение метода Крамера предполагает вычисление определителей различных матриц. Каждый определитель соотносится с неизвестной переменной системы. Решение системы уравнений находится путем деления определителя неизвестной переменной на определитель основной матрицы.
Рассмотрим пример системы уравнений:
| 2x + 3y + 4z = 10 |
| 5x + 6y + 7z = 20 |
| 8x + 9y + 10z = 30 |
Для применения метода Крамера составим матрицу системы:
| 2 | 3 | 4 |
| 5 | 6 | 7 |
| 8 | 9 | 10 |
Вычислим определитель основной матрицы системы:
det |2 3 4| = 2 * (6*10-7*9) - 3 * (5*10-7*8) + 4 * (5*9-6*8) = 12 - 9 + 6 = 9
Таким образом, определитель основной матрицы равен 9, что является ненулевым значением. Следовательно, система имеет единственное решение.
Вычислим определители матриц, соотносящиеся с неизвестными переменными:
det |10 3 4| = 10 * (6*10-7*9) - 3 * (20*10-7*8) + 4 * (20*9-6*8) = 600 - 480 + 720 = 840
det |2 10 4| = 2 * (20*10-7*8) - 10 * (6*10-7*9) + 4 * (6*8-20*9) = 240 - 90 - 72 = 78
det |2 3 10| = 2 * (5*10-7*9) - 3 * (20*10-7*8) + 10 * (20*9-6*8) = 12 - 120 + 840 = 732
Теперь можно найти значения неизвестных переменных:
x = det |10 3 4| / det |2 3 4| = 840 / 9 = 93.33
y = det |2 10 4| / det |2 3 4| = 78 / 9 = 8.67
z = det |2 3 10| / det |2 3 4| = 732 / 9 = 81.33
Таким образом, решением данной системы уравнений является:
x = 93.33
y = 8.67
z = 81.33








