Система неравенств – это математическое выражение, состоящее из двух и более неравенств. Решение системы неравенств является одной из важных тем в математике и широко используется в различных областях науки, экономики и инженерии.
Принцип решения системы неравенств состоит в нахождении всех значений переменных, при которых выполнены все неравенства системы. Это значит, что решение системы неравенств – это множество всех допустимых значений переменных, удовлетворяющих условиям всех неравенств.
Существует несколько методов решения системы неравенств, среди которых наиболее популярным является графический метод. Этот метод заключается в построении графиков каждого уравнения или неравенства системы на координатной плоскости и определении множества точек пересечения всех графиков. Таким образом, решение системы неравенств представляет собой область на координатной плоскости, в которой находятся все точки пересечения графиков.
В случае сложных систем неравенств, когда графический метод может быть неэффективен, применяются методы алгебраического решения, такие как метод подстановки, метод исключения и метод двух шагов. Все эти методы основаны на преобразованиях системы неравенств путем выражения одной переменной через другую и последующих подстановок и сравнений.
Общие принципы решения системы неравенств

Решение системы неравенств представляет собой процесс нахождения всех значений переменных, которые удовлетворяют всем неравенствам системы.
Для решения системы неравенств необходимо выполнить следующие шаги:
- Изучить все неравенства системы и определить их типы (строгие или нестрогие), а также знаки неравенств (больше, меньше, больше или равно, меньше или равно).
- Преобразовать неравенства таким образом, чтобы переменная находилась в левой части, а константа - в правой.
- Решить каждое неравенство по отдельности и найти интервалы или точки, удовлетворяющие неравенству.
- Определить пересечения и объединения интервалов, полученных в предыдущем шаге, чтобы получить окончательное решение системы неравенств.
После выполнения данных шагов можно сказать, что система неравенств решена. Ответом будет множество всех значений переменных, удовлетворяющих системе неравенств.
Важно помнить, что при совмещении интервалов и точек неравенства могут возникать условия совпадения и получения пустого множества решений. Поэтому рассмотрение каждой системы неравенств требует внимательности и аккуратности.
Метод графиков для решения системы неравенств
Для начала решения системы неравенств с помощью метода графиков необходимо:
- Записать систему неравенств в виде неравенств с переменными на одной стороне и нулем на другой.
- Построить графики каждой функции, заданной неравенством. Для этого необходимо найти корни каждого уравнения и определить их тип (точка, интервал, полуинтервал).
- Проанализировать графики функций и определить области, в которых выполняются все неравенства системы. Область, в которой все неравенства выполняются, будет общим решением системы.
Если графики функций никак не пересекаются, это означает, что система не имеет решений. Если же графики функций пересекаются в одной точке или пересекаются на каком-то интервале или полуинтервале, то решением системы будут все точки, лежащие в области пересечения.
Метод графиков позволяет наглядно представить решение системы неравенств и является удобным инструментом для решения простых систем. Однако он может оказаться неудобным в случае сложных систем с большим количеством переменных и неравенств.
Принципы решения системы неравенств путем приведения к эквивалентным уравнениям

Один из основных методов решения систем неравенств – приведение к эквивалентным уравнениям. Данный метод позволяет заменить неравенства эквивалентными им уравнениями, что упрощает дальнейший анализ системы и нахождение ее решений.
Для приведения неравенств к уравнениям, необходимо знать следующие принципы:
Правило 1:
Добавление или вычитание одного и того же числа к обеим сторонам неравенства не меняет его смысла. Если к каждому члену неравенства прибавить или вычесть одно и то же число, неравенство останется в силе. Например, из неравенства:
a > b,
можно получить эквивалентное уравнение:
a + c > b + c.
Правило 2:
Умножение или деление обеих сторон неравенства на положительное число не меняет его смысла. Если обе части неравенства поделить или умножить на одно и то же положительное число, неравенство сохранит свою силу. Например, из неравенства:
a > b,
можно получить эквивалентное уравнение:
ca > cb,
где c - положительное число.
Применение этих правил позволяет привести систему неравенств к эквивалентным уравнениям. Затем можно проанализировать полученные уравнения и определить их решения. В случае системы неравенств, это будут интервалы значений переменных, которые удовлетворяют всем уравнениям.
Метод подстановки для решения системы неравенств
Шаги метода подстановки:
- Выберите одно из уравнений системы и решите его относительно одной из переменных.
- Подставьте найденное значение переменной обратно в остальные уравнения системы.
- Проверьте каждое уравнение на соответствие.
- Если все уравнения выполняются, то найденное значение переменной является решением системы.
- Если хотя бы одно уравнение не выполняется, то найденное значение не является решением системы.
- Повторите шаги 1-5 для каждой переменной системы.
- Если для каждой переменной найдено решение, то решение системы состоит из найденных значений для всех переменных.
Применение метода подстановки требует внимательности и точности, так как на каждом шаге необходимо проверять соответствие всех уравнений системы.
Данный метод может быть полезен при решении системы неравенств, особенно при отсутствии более эффективных способов решения.
Решение системы неравенств методом интервалов
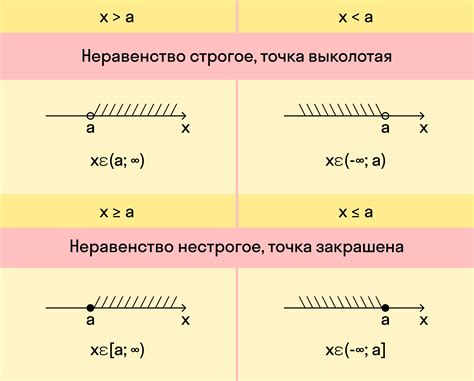
Для начала, систему неравенств необходимо привести к более простому виду, например, к виду x < a или x > b, где a и b - некоторые числа.
Затем необходимо рассмотреть все возможные комбинации интервалов, заданных неравенствами, и определить пересечение этих интервалов. Пересечение интервалов и будет являться множеством значений переменных, удовлетворяющих системе неравенств.
Для этого необходимо определить максимальный из левых концов интервалов и минимальный из правых концов интервалов для каждой переменной. Если максимальный левый конец меньше или равен минимальному правому концу, то данная переменная принадлежит найденному пересечению интервалов.
Таким образом, метод интервалов позволяет найти множество значений переменных, удовлетворяющих системе неравенств. Он широко применяется в различных областях, таких как математика, физика, экономика и другие.
Решение системы неравенств вещественными числами
Для решения системы неравенств вещественными числами следует учитывать следующие основные принципы и способы:
1. Определение области решений:
Первым шагом является определение области, в которой могут находиться значения переменных системы неравенств. Для этого нужно проанализировать все неравенства в системе и найти их пересечение. Отметим, что область решений может быть пустой.
2. Графическое представление решения:
Для более наглядного представления решения системы неравенств можно построить соответствующую графическую модель. На графике будут изображены все неравенства и их пересечение, то есть область решений. Этот метод позволяет лучше понять, какие значения переменных удовлетворяют системе неравенств.
3. Аналитическое решение:
Если у системы неравенств есть конкретное аналитическое решение, то можно его найти, используя алгебраические методы. Для этого нужно последовательно анализировать каждое неравенство и находить значения переменных, при которых каждое неравенство будет выполняться.
4. Проверка решения:
После нахождения аналитического решения необходимо проверить его, подставив найденные значения переменных в исходную систему неравенств. Если все неравенства выполняются при данных значениях, то решение является корректным.
Решение системы неравенств вещественными числами может быть достаточно сложной задачей, требующей внимательного анализа и применения различных математических методов. Однако, с помощью описанных принципов и способов можно упростить процесс решения и получить точные результаты.








