Пропорция – это математический термин, который обозначает равенство двух отношений. В школьной программе пропорции изучаются уже с 6 класса и являются одним из основных элементов курса арифметики.
Для решения пропорции необходимо знать несколько основных правил. Во-первых, отношения, стоящие в одном ряду, должны быть равными. Во-вторых, если в пропорции присутствует неизвестное значение, его можно найти с помощью простых математических операций.
Например, рассмотрим пропорцию: 2/5 = x/10. Чтобы найти значение x, нужно умножить 2 на 10 и разделить полученное число на 5. Таким образом, x = (2 * 10) / 5 = 4.
Решение пропорций может быть полезным во многих жизненных ситуациях, например, при расчете доли или процента. Умение работать с пропорциями позволяет быстро и точно решать различные математические задачи.
Пропорция в 6 классе: основные правила и примеры

Основное правило решения пропорции заключается в установлении равенства долей чисел. То есть, произведение a и d должно быть равно произведению b и c. Формула для этого выглядит так: a * d = b * c.
Для решения пропорции нужно найти значение одной неизвестной величины (a, b, c или d), зная значения остальных трех.
Например, рассмотрим следующую пропорцию:
1. Если a = 2, b = 4 и c = 6, то найдем значение d:
a * d = b * c
2 * d = 4 * 6
2d = 24
d = 12
Ответ: d = 12.
Таким образом, значение неизвестной величины d равно 12.
2. Если a=3, c=5 и d=7, то найдем значение b:
a * d = b * c
3 * 7 = b * 5
21 = 5b
b = 21/5
Ответ: b = 4.2.
Таким образом, значение неизвестной величины b равно 4.2.
Зная эти основные правила и примеры, вы уже можете решать пропорции в 6 классе и успешно выполнять соответствующие задания.
Определение пропорции
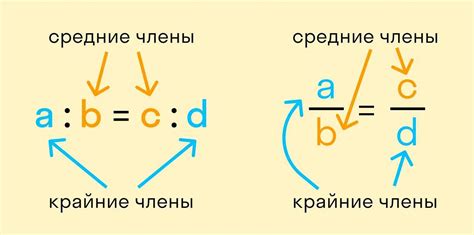
В числовом виде пропорция может быть записана в виде а:b = c:d, где a, b, c и d – это числа или величины. Здесь a и b являются частями, а c и d – целыми или полными, в которых требуется найти соответствующие части. Пропорция также может быть записана в виде дроби a/b = c/d или в виде уравнения ab = cd.
Пропорция позволяет найти неизвестные значения, если известны три из четырех элементов. Для решения пропорции можно использовать правило трех пропорций, когда известны три элемента, или правило перекрестных произведений, когда известны два элемента.
Например, если известно, что при 2 кг апельсинов стоимость составляет 150 рублей, можно использовать пропорцию для определения стоимости 4 кг апельсинов.
Примечание: Пропорция используется не только в математике, но и в различных областях жизни, таких как физика, химия, экономика и т. д. Понимание и умение работать с пропорциями являются важными навыками для решения различных задач.
Основные правила решения

Для решения пропорции в 6 классе нужно следовать нескольким основным правилам:
1. Запишите пропорцию с использованием знака равенства.
Пропорция представляет собой соотношение двух дробей или долей. Знак равенства показывает, что две доли или две дроби равны между собой.
2. Проверьте, можно ли сократить дроби.
Если в пропорции есть общие множители числителя и знаменателя, то их можно сократить. Сокращая дроби, вы получаете эквивалентную пропорцию с меньшими числами.
3. Решите пропорцию с помощью правила произведения.
Чтобы решить пропорцию, нужно умножить знаменатель одной доли или дроби на числитель другой доли или дроби. Результатом будет новая дробь или доля.
4. Проверьте правильность решения.
После решения пропорции проверьте, выполняется ли равенство. Для этого можно сравнить оба значения и убедиться, что они равны.
Следуя этим основным правилам, вы сможете успешно решать пропорции в 6 классе и использовать их в решении задач.
Первый пример пропорции
Дана пропорция: A/B = C/D
Нам известны значения A и B, и мы хотим найти значение C. Для этого мы можем использовать правило трёх, когда мы находим отношение между двумя известными значениями и затем умножаем или делим их на одно и то же число:
Сначала выразим C в виде формулы: C = (A * D) / B
Теперь подставим известные значения: C = (2 * 5) / 10
Выполняем вычисления: C = 10 / 10
Результат: C = 1
Ответ: значение C равно 1.
Второй пример пропорции:
Для более полного понимания, рассмотрим второй пример пропорции:
| Задача | Решение |
|---|---|
| Если 3 яблока стоят 150 рублей, сколько стоят 5 яблок? | Пусть х - стоимость 5 яблок. |
| Тогда пропорция будет выглядеть так: | 3 / х = 150 / 5 |
| Далее, упростим пропорцию: | 3 * 5 = х * 150 |
| Умножим обе стороны уравнения на 150: | 15 = х * 150 |
| Делим обе стороны на 150: | х = 15 / 150 |
| Итак, стоимость 5 яблок равна 0.1 рублей. |
Таким образом, стоимость 5 яблок составляет 0.1 рублей.
Третий пример пропорции
Рассмотрим следующий пример пропорции:
У Васи 3 зеленых шарика и 7 красных шариков. Сколько будет зеленых шариков у Васи, если он имел бы 15 красных шариков?
Чтобы решить эту пропорцию, нам нужно сравнить отношение количества зеленых шариков к количеству красных шариков в обоих случаях.
В начальной ситуации отношение зеленых шариков к красным составляет 3:7.
Давайте преобразуем эту пропорцию, чтобы найти количество зеленых шариков при 15 красных шариках.
- У Васи: Зеленые шарики / Красные шарики = 3 / 7
- При 15 красных шариках: Зеленые шарики / 15 = 3 / 7
Для решения этой пропорции мы можем использовать метод перекрестного умножения.
- 3 * 15 = Зеленые шарики * 7
- 45 = Зеленые шарики * 7
Чтобы найти количество зеленых шариков, мы делим обе стороны уравнения на 7:
- 45 / 7 = Зеленые шарики
- 6.42857 = Зеленые шарики
Таким образом, у Васи будет около 6 зеленых шариков, если он имел бы 15 красных шариков.
Четвертый пример пропорции:

Дана пропорция: 5 : 3 = 15 : x.
Для решения этой пропорции нужно установить соответствие между долями, высказать равенство этих долей и составить уравнение:
| 5 | : | 3 | = | 15 | : | x |
|---|
Далее, чтобы найти значение переменной x, нужно перекрестно умножить числа, находящиеся на противоположных сторонах уравнения:
| 5 * x | = | 3 * 15 |
|---|
Получаем уравнение:
| 5x | = | 45 |
|---|
Для того, чтобы найти значение переменной x, нужно поделить обе части уравнения на 5:
| x | = | 45 / 5 |
|---|
Итак, решение пропорции равно:
| x | = | 9 |
|---|
Таким образом, значение переменной x в данной пропорции равно 9.
Пятый пример пропорции
Рассмотрим пятый пример пропорции, чтобы лучше понять, как решать задачи этого типа.
| Товар | Количество | Цена |
|---|---|---|
| Молоко | 3 литра | 180 рублей |
| Сметана | 4 литра | 240 рублей |
Задача: сколько стоит 5 литров молока?
Для решения этой задачи воспользуемся пропорцией:
Количество товара 1 / Цена товара 1 = Количество товара 2 / Цена товара 2
В нашем случае:
3 литра / 180 рублей = 5 литров / Х рублей
Чтобы найти Х, умножим 180 на 5 и поделим на 3:
Х = (180 * 5) / 3 = 300 рублей
Таким образом, 5 литров молока стоят 300 рублей.
Используя эти примеры, вы можете научиться решать задачи с пропорциями в 6 классе и успешно справляться с ними в будущем.








