Решение неравенств – это один из основных элементов математики, который позволяет определить все значения переменных, удовлетворяющие условию неравенства. Неравенства часто встречаются в различных областях науки и повседневной жизни, поэтому важно уметь разбираться в их решении.
Для решения неравенств необходимо использовать определенные правила и методы. Самый простой способ – применить арифметические действия, аналогичные тем, которые используются при решении уравнений. Однако, при решении неравенств нужно учитывать знаки неравенства и выполнять необходимые дополнительные действия.
Например, рассмотрим неравенство x + 3 > 7. Сначала вычитаем 3 из обеих частей: x + 3 - 3 > 7 - 3. Получаем x > 4. Таким образом, все значения переменной x, большие 4, удовлетворяют данному неравенству.
Для решения неравенств существует несколько типов задач: неравенства с одной переменной, неравенства с несколькими переменными, неравенства с модулями и прочие. В каждом из этих случаев применяются различные методы и правила, которые помогут найти все значения переменных, удовлетворяющие неравенству.
В данной статье мы рассмотрим примеры решения различных типов неравенств и объясним основные шаги, которые нужно выполнить, чтобы получить правильный ответ. При этом мы покажем, что решение неравенств – это несложный процесс, доступный всем.
Что такое неравенства и как их решать

Решение неравенства заключается в нахождении всех или некоторых значений переменной, для которых неравенство выполняется. Чтобы решить неравенство, можно использовать различные методы, включая графический, алгебраический и численный методы.
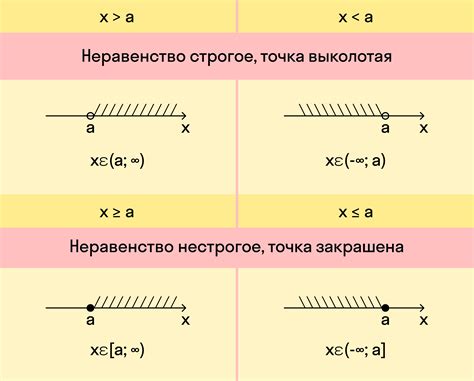
Графический метод заключается в построении графика неравенства на числовой оси и определении области, где выполняется неравенство. Область, где выполняется неравенство, может быть выражена как интервалы на числовой оси или в виде геометрической области на плоскости.
Алгебраический метод включает в себя преобразование неравенства таким образом, чтобы переменная осталась слева от знака неравенства. Затем решается алгебраическое уравнение для переменной и определяется область значений, удовлетворяющая неравенству.
Численный метод может быть использован, когда графическое или алгебраическое решение неравенства затруднено или невозможно. В этом случае используются методы численного анализа, чтобы получить аппроксимацию решения неравенства.
Для решения неравенств необходимо учитывать особенности использованных знаков сравнения. Например, при умножении или делении обеих частей неравенства на отрицательное число, необходимо изменить направление неравенства.
Решение неравенств позволяет определить интервалы или значения, для которых выполняется заданное условие. Это важный инструмент в математике и науках, где требуется анализ количественных соотношений и ограничений.
Определение неравенств и их примеры
Примеры неравенств:
- 2x + 3 > 7: решением этого неравенства является любое значение x, большее чем 2.
- -5x ≤ 10: решением этого неравенства является любое значение x, меньшее или равное -2.
- x/4
- 2x - 3 ≥ 9: решением этого неравенства является любое значение x, большее или равное 6.
При решении неравенств нужно учитывать порядок операций и правила замены знаков при умножении или делении на отрицательное число. Также важно помнить, что некоторые значения переменной могут привести к недопустимым решениям, например, к делению на ноль.
Методы решения неравенств
Существуют различные методы решения неравенств, каждый из которых применяется в зависимости от вида и условий задачи. Ниже рассмотрены основные методы:
| Метод | Описание |
|---|---|
| Метод подстановки | Один из наиболее простых методов решения неравенств. При этом подставляются значения переменной из области определения неравенства и проверяется выполняется ли неравенство для данного значения. |
| Метод интервалов | При использовании этого метода, область значений переменной разбивается на интервалы, для каждого из которых определяется, какое условие (больше или меньше) выполняется. Полученные интервалы объединяются для получения окончательного решения неравенства. |
| Метод значений | В этом методе задача сводится к определению значений переменной, для которых выполняется неравенство. Используются различные методы анализа функций и графиков. |
| Метод допустимых значений | Для решения неравенств используются ограничения, установленные на переменные. Значения переменной, которые удовлетворяют ограничениям, являются допустимыми и используются при решении неравенства. |
Выбор метода решения неравенства зависит от его вида и условий задачи. Важно учитывать, что при применении некоторых методов могут получаться дополнительные условия, которые необходимо учесть в окончательном ответе.








