Линейная функция является одной из основных функций в математике. Она представляет собой функцию вида y = kx + b, где k и b - константы, а x - переменная. Зная значения k, b и x, можно найти значение функции y. В данной статье мы рассмотрим несколько методов нахождения значения линейной функции и приведем примеры.
Первый метод - метод подстановки. Для этого необходимо уравнение линейной функции y = kx + b, подставить вместо x значение переменной, и вычислить результат. Например, если дана линейная функция y = 2x + 3, а переменная x равна 5, то значение функции можно найти следующим образом: подставляем x = 5 вместо x и выполняем вычисления: y = 2 * 5 + 3 = 13.
Второй метод - метод графической интерпретации. Для этого необходимо построить график линейной функции на координатной плоскости. Зная значение переменной x, находим соответствующую точку на графике и опускаем от нее вертикальную прямую на ось y. Точка пересечения этой вертикальной прямой с осью y и будет значением функции y. Например, если график линейной функции пересекает ось y в точке (0, 2), то значение функции при x = 0 будет равно 2.
Важно помнить, что значение b в уравнении y = kx + b представляет собой значение функции при x = 0. Это называется свободным членом уравнения и указывает на точку пересечения графика функции с осью y.
Найденные значения линейной функции могут быть использованы для решения различных задач и применений математики в реальной жизни, таких как расчеты финансовых данных, прогнозирование развития процессов и т.д. Поэтому умение находить значения линейной функции является важным навыком в математике и на первый взгляд может показаться сложным, однако с практикой и пониманием основных методов, это становится более простым и понятным.
Что такое линейная функция?
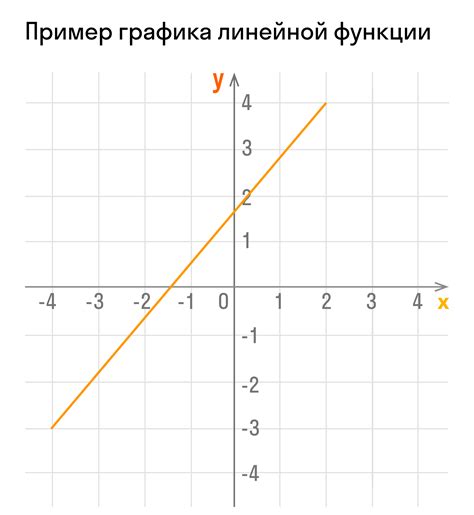
Линейная функция имеет простую структуру и характеризуется тем, что каждому значению x соответствует только одно значение y. График линейной функции - это прямая линия, которая не имеет изгибов и изменяет свое положение в пространстве в зависимости от значений переменных x и y.
С помощью линейной функции можно решать различные задачи, связанные со смешанными уравнениями, прогнозированием тенденций, нахождением коэффициента наклона и точки пересечения прямой с осью y. Линейные функции широко применяются в физике, экономике, статистике, технике и других областях науки и практики.
Кроме того, линейная функция является одной из базовых функций при изучении математики и алгебры. Она позволяет понять и описать зависимость между переменными и наглядно представить ее на графике. Поэтому понимание линейных функций основательно важно для развития математической грамотности и навыков решения задач в реальной жизни.
Значение линейной функции: определение
Значение линейной функции определяется подстановкой значения переменной x в уравнение и получением соответствующего значения переменной y. Другими словами, для заданного значения x нужно найти соответствующее значение функции y.
Процесс определения значения линейной функции может быть выполнен с помощью нескольких методов, таких как:
- Подстановка значения x в уравнение и вычисление значения y.
- Графическое представление функции на координатной плоскости и нахождение соответствующего значения по оси y.
- Таблица значений, где каждой паре значений x и y соответствует строка таблицы.
Например, для уравнения y = 3x + 2, если нам необходимо найти значение функции при x = 4, мы можем подставить значение в уравнение:
y = 3 * 4 + 2 = 12 + 2 = 14
Таким образом, при x = 4, значение функции будет равно y = 14.
Что такое аргумент и параметр в линейной функции?
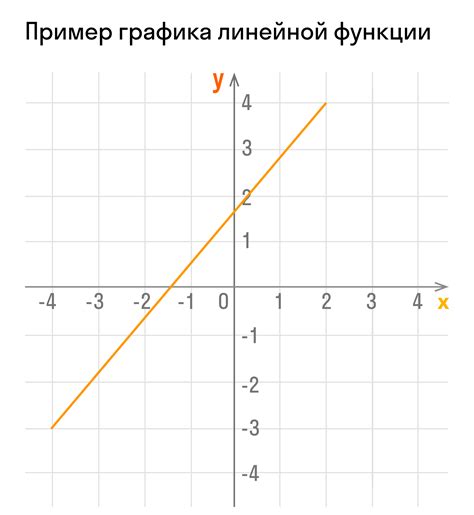
Аргументом линейной функции является независимая переменная, которая влияет на значение функции. Он обычно обозначается буквой "x" и представляет собой значение, которое мы подставляем в функцию для получения соответствующего значения функции.
Параметр, с другой стороны, является коэффициентом функции, который определяет ее характеристики. Он обычно обозначается буквой "a" и определяет наклон линии графика функции. Значение параметра влияет на угол наклона графика: если значение положительное, график будет стремиться вверх, а если отрицательное, график будет стремиться вниз.
Таким образом, использование аргумента и параметра позволяет нам определить точку на графике линейной функции и вычислить соответствующее значение функции для этой точки.
Метод подстановки для нахождения значения линейной функции
Чтобы найти значение линейной функции при заданном значении аргумента, нужно подставить его значение вместо x в уравнение функции и вычислить значение y. Например, если у нас есть функция y = 2x + 3, и нужно найти значение функции при x = 5, мы подставим значение x в уравнение и получим y = 2 * 5 + 3 = 13.
Применение метода подстановки позволяет быстро и удобно находить значения линейной функции в различных ситуациях, например, при решении задач по геометрии, экономике или физике.
Примеры применения метода подстановки

Рассмотрим пример. Дана линейная функция f(x) = 2x - 3. Найдем значение этой функции при x = 5. Для этого подставим значение переменной в уравнение:
f(5) = 2 * 5 - 3
Далее выполняем простые арифметические операции:
f(5) = 10 - 3 = 7
Таким образом, при x = 5 значение функции будет равно 7.
Метод подстановки особенно полезен при решении систем линейных уравнений. В этом случае можно поочередно подставлять значения переменных и упрощать уравнения до нахождения решения.
Метод графического нахождения значения линейной функции
Для нахождения значения линейной функции графическим методом нужно построить график этой функции на координатной плоскости. Линейная функция представляет собой прямую линию, которая имеет угловой коэффициент (наклон) и точку пересечения с осью ординат (начало отсчета).
Чтобы найти значение функции для конкретного значения аргумента, нужно отложить этот аргумент на оси абсцисс и провести вертикальную линию (перпендикулярную оси абсцисс) от этой точки до графика функции. Точка пересечения этой линии с графиком будет соответствовать значению функции для данного аргумента.
Если график линейной функции является уголком, то значение функции будет совпадать с координатой y точки пересечения. Если график пересекает ось абсцисс или имеет касательную, то значение функции будет равно нулю.
Пример:
- Для линейной функции y = 2x - 1 найти значение функции при x = 3.
- Откладываем точку x = 3 на оси абсцисс.
- Проводим вертикальную линию от этой точки до графика функции.
- Определяем координаты точки пересечения линии с графиком функции.
- Значение функции для x = 3 будет равно координате y этой точки.
- y = 2 * 3 - 1 = 6 - 1 = 5.
Таким образом, значение линейной функции y = 2x - 1 при x = 3 равно 5.
Примеры применения метода графического нахождения значения линейной функции
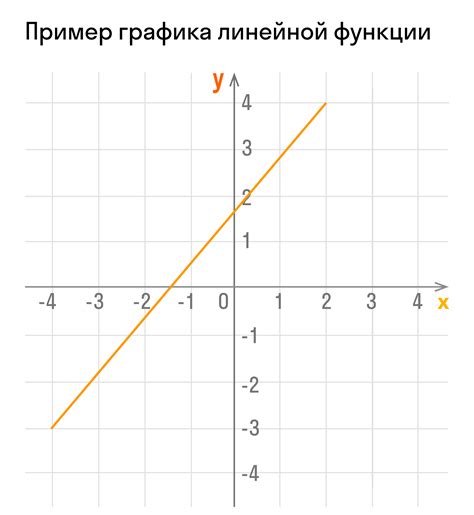
Метод графического нахождения значения линейной функции позволяет наглядно представить зависимость между переменными и найти значение функции путем построения графика и определения координаты точки.
Рассмотрим несколько примеров применения этого метода:
Пример 1:
Дана линейная функция f(x) = 2x + 3. Найдем значение функции при x = 5.
1. Построим график функции:
- Выберем систему координат на плоскости;
- Проведем ось OX (горизонтальная ось) и ось OY (вертикальная ось);
- Поставим точку O в начале координат;
- Проведем прямую, соответствующую уравнению f(x) = 2x + 3.
2. Определим координаты точки с x = 5:
- Примем x = 5;
- Проведем вертикальную прямую из точки x = 5 и определим точку пересечения с графиком функции;
- Определим соответствующее значение y для данной точки.
3. Запишем полученный результат: значение функции f(x) при x = 5 составляет y = 2 * 5 + 3 = 13.
Пример 2:
Дана линейная функция g(x) = -3x + 7. Найдем значение функции при x = -2.
1. Построим график функции:
- Выберем систему координат на плоскости;
- Проведем ось OX (горизонтальная ось) и ось OY (вертикальная ось);
- Поставим точку O в начале координат;
- Проведем прямую, соответствующую уравнению g(x) = -3x + 7.
2. Определим координаты точки с x = -2:
- Примем x = -2;
- Проведем вертикальную прямую из точки x = -2 и определим точку пересечения с графиком функции;
- Определим соответствующее значение y для данной точки.
3. Запишем полученный результат: значение функции g(x) при x = -2 составляет y = -3 * (-2) + 7 = 13.
Таким образом, метод графического нахождения значения линейной функции является простым и эффективным способом определения значения функции при заданном аргументе. Он позволяет наглядно представить зависимость и найти значение функции с помощью графика, что особенно полезно при решении задач на переменные и функции.
Метод аналитического нахождения значения линейной функции
Для применения этого метода необходимо знать уравнение линейной функции вида y = kx + b, где k – наклон прямой, а b – свободный коэффициент.
Для нахождения значения линейной функции в данном методе необходимо:
- Определить значения k и b в уравнении функции.
- Подставить значение переменной x в уравнение.
- Вычислить значение y.
Например, у нас есть линейная функция y = 2x + 3. Чтобы найти значение функции при x = 4, необходимо подставить это значение в уравнение:
y = 2 * 4 + 3 = 8 + 3 = 11.
Таким образом, при x = 4 значение функции равно 11.
Метод аналитического нахождения значения линейной функции является простым и позволяет быстро определить значение функции для заданного значения переменной. Он широко используется в математике и в реальных задачах, требующих расчетов с линейными функциями.
Примеры применения метода аналитического нахождения значения линейной функции
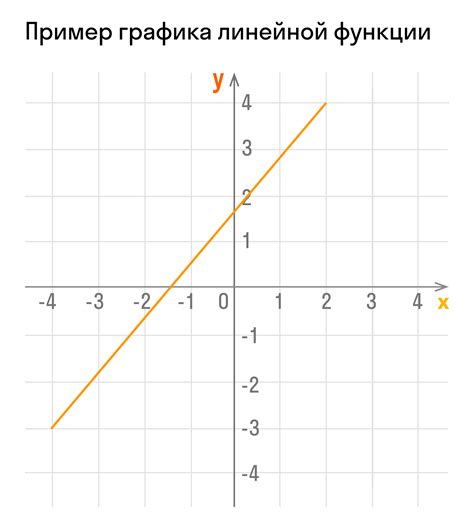
Метод аналитического нахождения значения линейной функции позволяет определить точное значение функции при заданных значениях аргументов. Рассмотрим несколько примеров применения этого метода.
- Пример 1: Дана линейная функция f(x) = 2x + 3. Найдем значение функции при x = 5. Подставим значение аргумента в формулу функции: f(5) = 2 * 5 + 3 = 13. Таким образом, значение функции при x = 5 равно 13.
- Пример 2: Рассмотрим линейную функцию g(t) = -0.5t - 2. Найдем значение функции при t = -4. Подставим значение аргумента в формулу функции: g(-4) = -0.5 * (-4) - 2 = 0. Таким образом, значение функции при t = -4 равно 0.
- Пример 3: Исследуем линейную функцию h(y) = 3y. Найдем значение функции при y = 0. Подставим значение аргумента в формулу функции: h(0) = 3 * 0 = 0. Таким образом, значение функции при y = 0 равно 0.
Таким образом, метод аналитического нахождения значения линейной функции позволяет получить точные результаты при заданных значениях аргументов. Он является одним из основных инструментов в аналитическом решении задач, связанных с линейными функциями.
Выводы и рекомендации
Подстановка значений особенно полезна, когда известны значения переменных, а нужно найти значение функции. Этот метод прост в использовании и может быть применен в любой ситуации.
Использование графика также является эффективным способом нахождения значения линейной функции. Построение графика позволяет наглядно представить связь между переменными и функцией.
Рекомендуется использовать подстановку значений при нахождении значения линейной функции в простых ситуациях, а использовать график при решении более сложных задач.
Также рекомендуется проверять полученный результат: подставлять найденное значение в исходное уравнение и проверять, что равенство выполняется. Это поможет избежать ошибок и убедиться в правильности ответа.
В заключение, знание методов нахождения значения линейной функции является важным навыком при решении задач из различных областей, таких как математика, экономика, физика и другие. Выбор метода зависит от сложности задачи и предпочтений пользователя.








