Одной из основных задач математического анализа является поиск нулей функции. Ноль функции - это такая точка, при которой значение функции равно нулю. Нули функции играют важную роль в различных областях науки и техники, поэтому методы их нахождения также являются важными. В этой статье мы рассмотрим основные методы нахождения нулей функции и приведем примеры их применения.
Первым методом для поиска нулей функции является графический метод. Суть его заключается в построении графика функции и нахождении точек пересечения графика с осью абсцисс. Если в области интересующего нас значения функции происходит пересечение с осью абсцисс, то данная точка будет нулем функции. Графический метод позволяет получить нули функции с достаточной точностью и приближенности, однако этот метод не всегда применим, особенно если функция имеет сложный вид или необходимо получить значения с большей точностью.
Вторым методом является аналитический метод. Он заключается в алгебраических преобразованиях и применении различных теорем для нахождения нулей функции. Для этого необходимо решить уравнение, заданное в виде функции равной нулю. Аналитический метод позволяет получить точные значения нулей функции, однако его применение может быть затруднено, если функция имеет сложную формулу или не может быть решена аналитически.
Третьим методом является численный метод. Он основан на построении численной последовательности значений функции и нахождении точек, в которых значения функции близки к нулю. К численным методам относятся метод половинного деления, метод Ньютона и многие другие. Численные методы являются эффективными и универсальными, позволяющими находить нули функции с высокой точностью и использовать их для дальнейших вычислений или аппроксимаций. Однако численные методы требуют некоторых вычислительных ресурсов и времени для выполнения.
Определение нулей функции
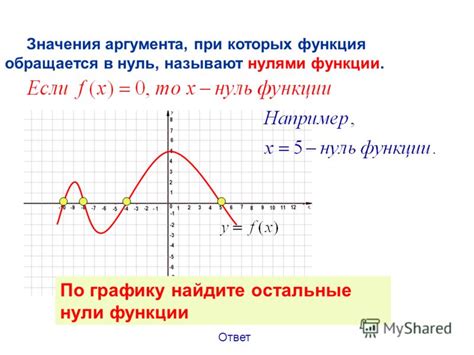
Определение нулей функции можно найти, решая уравнение, полученное приравниванием функции к нулю:
| Если функция задана явно: | Функция равна нулю: $f(x) = 0$ |
| Если функция задана графически: | Найти точки пересечения графика функции с осью OX. В этих точках $y = 0$, следовательно, функция обращается в ноль. |
| Если функция задана в виде таблицы значений: | Найти значения аргумента, при которых соответствующие значения функции равны нулю. |
Методы нахождения нулей функции
При решении задач на нахождение нулей функции существует несколько распространенных методов. Ниже приведены основные из них:
1. Метод графического представления
Метод графического представления основан на построении графика функции и определении точек пересечения графика с осью абсцисс. Нули функции соответствуют точкам, где график функции пересекает ось абсцисс.
2. Метод подстановки
Метод подстановки заключается в подстановке различных значений аргумента в функцию и определении соответствующих значений функции. Нули функции соответствуют значениям аргумента, при которых функция равна нулю.
3. Метод численного решения
Метод численного решения основан на последовательном приближении к нулю функции с помощью численных алгоритмов. Наиболее распространенные методы численного решения включают метод бисекции, метод Ньютона и метод касательных.
4. Метод аналитического решения
Метод аналитического решения основан на выполнении аналитических преобразований и алгебраических операций с функцией. Для некоторых видов функций существуют специальные методы нахождения нулей.
При выборе метода нахождения нулей функции следует учитывать сложность функции, доступность математических инструментов и требования по точности результата.
Метод графика
Для применения метода графика необходимо построить график функции на координатной плоскости. Для этого можно использовать компьютерные программы или ручной способ с помощью координатной сетки и визуализации значений функции для различных аргументов.
На графике функции необходимо найти точки, в которых она пересекает ось абсцисс. Такие точки соответствуют нулевым значениям функции и являются ее нулями. То есть, если функция принимает значение ноль в точке (x, 0), то x - нуль функции.
Метод графика особенно удобен, если функция имеет простую геометрическую интерпретацию или содержит выражение, которое можно легко проанализировать и найти точки пересечения с осью абсцисс. Однако, этот метод может быть сложным или неэффективным для функций, у которых график имеет сложную форму или функции с большим количеством пересечений.
Метод графика является приближенным и не даёт точного значения нуля функции. Однако, он позволяет оценить расположение и количество нулей функции, что помогает при более точном применении других методов нахождения нулей, например, метода итераций или бисекции.
Ниже приведена таблица с примерами функций и их нулей, найденных с помощью метода графика.
| Функция | Нули |
|---|---|
| x^2 - 4 | -2, 2 |
| sin(x) | 0, π, 2π, 3π, ... |
| x^3 + 2x^2 - 3x - 10 | -2, 1, 5 |
Метод подстановки
Для применения метода подстановки следует выбрать подходящее значение переменной, которое легко можно подставить в уравнение и вычислить значение функции. После вычисления значения функции с подставленной переменной, следует решить полученное уравнение относительно переменной. Таким образом, найденное значение переменной будет являться одним из нулей функции.
Примером применения метода подстановки может служить уравнение: f(x) = x^2 - 5x + 6 = 0. Применим метод подстановки для переменной x = 2:
Подставляем значение x = 2 в уравнение: f(2) = 2^2 - 5 * 2 + 6 = 0. Вычисляем: f(2) = 4 - 10 + 6 = 0.
Полученное уравнение f(2) = 0 можно решить относительно переменной x для нахождения нулей функции.
Метод деления отрезка пополам
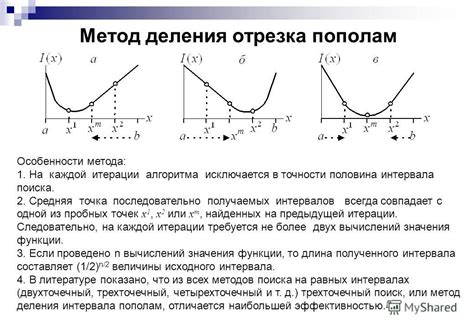
Принцип метода заключается в том, что на каждой итерации отрезок, содержащий корень функции, делится пополам, а затем выбирается тот из двух подотрезков, на концах которого знаки функции разных значений. Таким образом, на каждой итерации отрезок, содержащий корень, становится в два раза меньше.
Процесс деления отрезка пополам можно представить в виде таблицы:
| Шаг | Отрезок | Значение функции на отрезке |
|---|---|---|
| 1 | [a, b] | f(a) * f(b) |
| 2 | [a, c] или [c, b] | f(c) * f(a) или f(c) * f(b) |
| 3 | [a1, c1] или [c1, c] | f(a1) * f(c1) или f(c1) * f(c) |
| 4 | ... | ... |
По завершении необходимого количества итераций или при достижении необходимой точности, получается приближенное значение корня функции.
Метод деления отрезка пополам прост в реализации, но может потребовать большого числа итераций в случае, если функция имеет много корней или значения функции меняются быстро на отрезке. В таких случаях рекомендуется использовать более эффективные методы, такие как метод Ньютона или метод простой итерации.
Метод Ньютона
Для того чтобы применить метод Ньютона, необходимо иметь начальное приближение корня функции, которое можно выбрать, например, путем графического анализа функции или с помощью других методов.
Алгоритм метода Ньютона можно описать следующими шагами:
- Выбрать начальное приближение корня функции.
- Найти касательную к графику функции в заданной точке, используя производную функции.
- Найти точку пересечения касательной с осью абсцисс.
- Повторять шаги 2-3 до тех пор, пока не будет достигнута требуемая точность или не будет достигнуто максимальное количество итераций.
Метод Ньютона обладает высокой скоростью сходимости и может быть эффективным для нахождения корней функций, если исходное приближение корня достаточно близко к истинному значению. Однако он может не сойтись или сойтись к неверному корню, если начальное приближение выбрано неправильно или если функция имеет несколько корней вблизи исходного приближения.
Применение метода Ньютона требует вычисления производной функции, что может быть затруднительным в некоторых случаях. В таких случаях можно использовать численные методы для приближенного вычисления производной.
Пример использования метода Ньютона:
- Рассмотрим функцию f(x) = x^2 - 4.
- Выберем начальное приближение корня, например, x0 = 3.
- Вычислим производную функции: f'(x) = 2x.
- Найдем точку пересечения касательной с осью абсцисс: x1 = x0 - f(x0) / f'(x0) = 3 - (3^2 - 4) / (2 * 3) = 3 - (9 - 4) / 6 = 3 - 5 / 6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 - 5/6 = 3 - 5/6 - 5/6 = 3 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 = 3 - 5/6 3/6 - 5/6 = 3 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/6 - 5/
Метод простых итераций
Идея метода заключается в приведении исходного уравнения f(x) = 0 к виду x = g(x), где g(x) - некоторая функция. Затем начальное приближение x_0 выбирается произвольно, и далее на каждой итерации вычисляется следующее приближение по формуле x_{n+1} = g(x_n). Процесс итераций продолжается до достижения заданной точности или выполнения другого критерия остановки.
Ниже приведен алгоритм метода простых итераций:
- Выбрать начальное приближение x_0.
- Вычислить следующее приближение по формуле x_{n+1} = g(x_n).
- Повторять шаг 2 до достижения необходимой точности или выполнения другого критерия остановки.
- Вывести найденное приближение, которое будет являться нулем функции с заданной точностью.
Метод простых итераций имеет некоторые ограничения, такие как необходимость выбора подходящей функции g(x) и установление правильного критерия остановки. В случае, если функция g(x) выбрана неправильно или критерий остановки не удовлетворяет требованиям, метод может не сойтись к корню или сойтись медленно.
Использование метода простых итераций требует некоторых навыков программирования и математических знаний, но позволяет эффективно находить корни функций. Для решения сложных и нетривиальных уравнений часто используются более сложные итерационные методы, но метод простых итераций остается одним из основных инструментов в арсенале математиков и программистов.
Примеры решения
Для демонстрации основных методов нахождения нулей функции рассмотрим несколько примеров.
Пример 1:
Решим уравнение f(x) = x^2 - 4 методом подстановки. Для этого подставим значения из области определения функции и найдем соответствующие значения функции:
f(0) = (0)^2 - 4 = -4
f(1) = (1)^2 - 4 = -3
f(2) = (2)^2 - 4 = 0
f(3) = (3)^2 - 4 = 5
Таким образом, уравнение имеет два корня: x = 2 и x = -2.
Пример 2:
Решим уравнение g(x) = 2x^3 - 3x^2 - 12x графическим методом. Построим график функции и найдем точки, в которых график пересекает ось абсцисс:
Из графика видно, что уравнение имеет три корня: x = 0, x = 2 и x = -3.
Пример 3:
Решим уравнение h(x) = e^x - 5 методом итераций. Для этого используем итерационную формулу xn+1 = e^xn - 5:
Начальное приближение: x0 = 0
Подставляем значения в формулу:
x1 = e^0 - 5 = -4
x2 = e^(-4) - 5 = -5.982
x3 = e^(-5.982) - 5 = -5.9996
Продолжаем итерацию до достижения необходимой точности. Получаем приближенное значение корня уравнения: x ≈ -6.










