Функция - понятие, широко используемое в математике, информатике и других науках. Функция может быть обратимой, то есть такой, у которой на каждый элемент из области значений существует только одно значение из области определения.
Для того чтобы функция была обратимой, она должна быть инъективной, то есть каждому элементу из области значений функции должен соответствовать только один элемент из области определения. Если есть элемент из области значений, которому соответствует более одного элемента из области определения, то функция не является обратимой.
Например, функция "возведение в квадрат" является обратимой, так как каждому значению из области значений соответствует только одно значение из области определения. Но функция "взятие квадратного корня" не является обратимой, так как некоторым значениям из области значений соответствуют два значения из области определения (например, оба 2 и -2 соответствуют значению 4).
В математике существует несколько способов проверки обратимости функции. Один из них - использование понятия обратной функции, которая является обратимой для исходной функции. Если для функции f(x) существует обратная функция g(x), то f(x) является обратимой. Обратная функция g(x) с помощью композиции функций f(g(x)) = x и g(f(x)) = x выполняет обратное отображение.
Функции встречаются во многих областях науки и техники. Обратимость функции играет важную роль в различных приложениях, например, в криптографии для шифрования и дешифрования данных. Поэтому понимание и изучение обратимости функций является важной задачей для математиков и специалистов в области информационных технологий.
Что такое обратимая функция в математике?
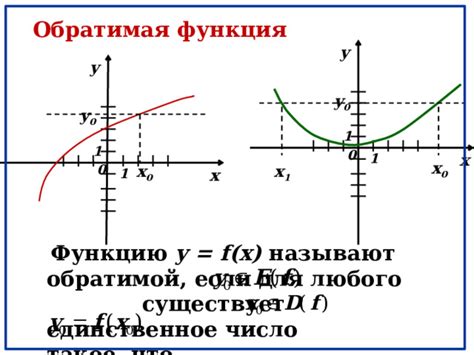
В математике обратимой функцией называется функция, которая имеет обратную функцию. Объяснить это понятие можно следующим образом: если заданная функция преобразует каждое значение из области определения в уникальное значение в области значений, то обратная функция преобразует каждое значение из области значений обратно в уникальное значение в области определения.
Математически обратная функция определяется следующим образом: пусть у нас есть функция f, которая преобразует значение x в значение y. Обратная функция f^(-1) обладает свойством f^(-1)(f(x)) = x для любого значения x из области определения. В других словах, применение функции f и ее обратной функции f^(-1) друг к другу должно дать исходное значение.
Примером обратимой функции может служить функция f(x) = 2x, где умножение на 2 преобразует значение x в значение y. Ее обратная функция f^(-1)(x) = x/2, где деление на 2 преобразует значение x обратно в значение y. Если мы применим функцию f и ее обратную функцию f^(-1) друг к другу, то получим исходное значение: f^(-1)(f(x)) = x/2 * 2x = x.
Обратимая функция является важным понятием в математике, так как она позволяет решать уравнения, находить обратные преобразования и выполнять другие математические операции.
Определение обратимой функции
Функция называется обратимой, если каждому значению ее аргумента соответствует единственное значение ее образа, и каждому значению образа соответствует единственное значение аргумента.
Математически это можно записать следующим образом:
- Если для функции f(x) существует функция g(x) такая, что f(g(x)) = x для всех x в области определения f, и g(f(x)) = x для всех x в области определения g, то f является обратимой функцией и g называется обратной функцией к f.
- Таким образом, обратная функция позволяет восстановить значение аргумента по значению образа.
Примеры обратимых функций:
- Линейные функции: f(x) = ax + b, где a и b - константы, и a ≠ 0. Обратная функция будет иметь вид g(x) = (x - b) / a.
- Квадратные функции: f(x) = x^2. Обратная функция будет иметь вид g(x) = √x.
- Тригонометрические функции: sin(x), cos(x), tg(x), ctg(x) при ограничениях на область определения. Обратные функции будут иметь вид arcsin(x), arccos(x), arctg(x), arcctg(x).
Примеры обратимых и необратимых функций
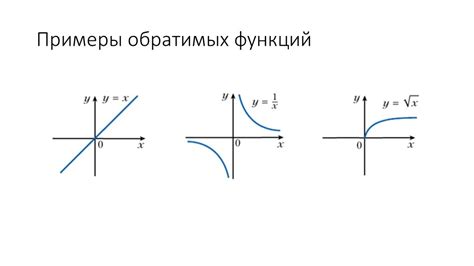
Примеры обратимых функций:
- Линейная функция y = kx + b, где k и b - константы. Для любого значения x существует единственное значение y, такое что при подстановке обратно в функцию получается исходное значение x.
- Функция возведения в квадрат x^2. Каждый элемент области определения функции имеет единственный элемент области значений, так что при подстановке обратно в функцию получается исходный элемент.
Необратимая функция - это функция, у которой для некоторых элементов области определения не существует элемента области значений, при подстановке которого в функцию получится исходный элемент.
Примеры необратимых функций:
- Функция возведения в степень x^n, где n - нечетное число. Например, при возведении отрицательного числа в нечетную степень, функция необратима, так как не существует действительных чисел, для которых такая степень будет отрицательным числом.
- Тригонометрические функции, такие как синус, косинус и тангенс. Эти функции являются периодическими, и для некоторых значений области определения не существует единственного элемента области значений.








