Монотонная функция - это функция, которая сохраняет порядок возрастания или убывания при изменении значения аргумента. Иными словами, если увеличение значения аргумента ведет к увеличению значения функции, то функция является возрастающей. Если увеличение значения аргумента ведет к уменьшению значения функции, то функция является убывающей.
Одна из особенностей монотонных функций заключается в том, что они не меняют свой порядок возрастания или убывания при замене коэффициентов или добавлении произвольного слагаемого. Это свойство позволяет использовать монотонные функции во многих областях, включая математический анализ, экономику, финансы и другие.
Применение монотонных функций находит свое применение в таких областях, как оптимизация, определение условий экстремума, решение неравенств, построение дифференциальных уравнений, анализ финансовых и экономических данных. Также монотонные функции используются при моделировании различных процессов и явлений, например, в космологии, физике, социологии и других науках.
Что значит монотонность функции: основные понятия и определения
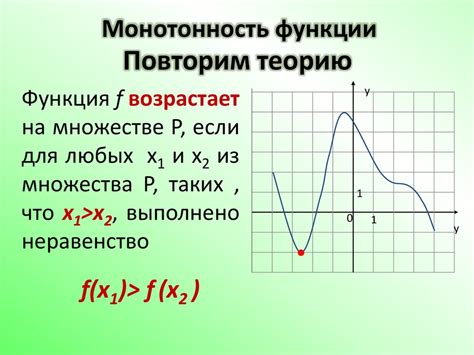
Функция называется неубывающей, если она сохраняет или увеличивает значения при изменении аргумента, и неубывающей, если она сохраняет или убывает значения при изменении аргумента.
Функцию можно определить как монотонную на промежутке, если она сохраняет порядок возрастания или убывания на этом промежутке.
Монотонность функции является важным свойством при изучении ее поведения. Она позволяет определить точки экстремумов, нулей и других особенностей функции.
Понимание монотонности функции помогает решать задачи оптимизации, анализовать изменение величин и прогнозировать тенденции в различных областях, таких как экономика, физика и теория вероятностей.
Понятие монотонности в математике
Если функция монотонно возрастает, это означает, что при увеличении значения аргумента значение функции также увеличивается. Например, функция y = x^2 является монотонно возрастающей на всем своем области определения, так как с ростом значения x значение y также увеличивается.
Если функция монотонно убывает, это означает, что при увеличении значения аргумента значение функции уменьшается. Например, функция y = -x является монотонно убывающей на всем своем области определения, так как с ростом значения x значение y уменьшается.
Функция, которая остается постоянной при изменении аргумента, называется постоянной функцией и является частным случаем монотонности. Например, функция y = 3 является постоянной функцией, так как ее значение не зависит от значения аргумента x.
Монотонность функции позволяет анализировать ее поведение и предсказывать значения функции при изменении аргумента. Также монотонность является важным свойством при решении уравнений и определении экстремумов.
Как определить монотонность функции на промежутке
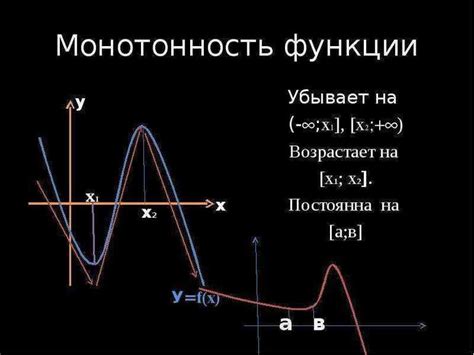
Для определения монотонности функции на промежутке можно использовать различные методы. Один из них - это использование производной функции. Если производная функции положительна на всем промежутке, то функция монотонно возрастает. Если производная функции отрицательна на всем промежутке, то функция монотонно убывает. Если производная функции равна нулю на всем промежутке, то функция может быть монотонной или иметь экстремумы, и для более точного определения монотонности следует исследовать саму функцию.
Другой метод - это использование знаков функции. Для этого необходимо вычислить значения функции на концах промежутка и в произвольной точке внутри промежутка. Затем сравнить полученные значения. Если значения возрастают вместе с аргументом на всем промежутке, функция монотонно возрастает. Если значения убывают вместе с аргументом на всем промежутке, функция монотонно убывает. Если значения не возрастают и не убывают, функция монотонно невозрастает или невозрастает.
Определение монотонности функции на промежутке важно для анализа поведения функции и понимания ее характеристик. Знание о монотонности функции может помочь в определении ее экстремумов, понимании изменения функции при изменении аргумента и выполнении других задач в области математики, физики, экономики и других наук.
Как выявить возрастание и убывание функции
Чтобы выявить, является ли функция монотонно возрастающей или монотонно убывающей, необходимо анализировать ее производную. Если производная функции положительна на всем промежутке, значит функция монотонно возрастает. Если производная функции отрицательна на всем промежутке, значит функция монотонно убывает. Если же производная функции меняет знак на промежутке, то функция немонотонна.
Для определения монотонности функции можно применить следующие шаги:
- Вычислить производную функции.
- Найти все точки, в которых производная обращается в ноль. Эти точки называются стационарными точками.
- Построить таблицу знаков производной функции на интервалах, образованных стационарными точками.
Если на каждом интервале таблицы знаков производной функции стоит "+" или "-" (в зависимости от знака производной), то функция будет монотонно возрастающей или монотонно убывающей на соответствующем промежутке. Если таблица знаков имеет разные знаки на разных интервалах, то функция будет немонотонной.
Таким образом, анализ производной позволяет определить возрастание или убывание функции и помогает в понимании ее поведения на заданной области определения.
Методы доказательства монотонности функции
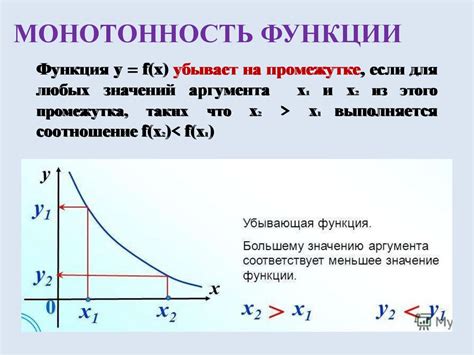
- Аналитический метод. При использовании этого метода необходимо анализировать производную функции. Если производная положительна на всем промежутке, то функция является возрастающей. Если производная отрицательна, то функция является убывающей. Если же производная равна нулю, то функция является константной.
- Геометрический метод. При использовании этого метода необходимо построить график функции и проанализировать его поведение на заданном промежутке. Если график функции идет вверх (имеет положительный наклон), то функция возрастает. Если график функции идет вниз (имеет отрицательный наклон), то функция убывает. Если же график функции горизонтален (имеет нулевой наклон), то функция является константной.
- Использование интервалов. При использовании этого метода необходимо разбить промежуток, на котором необходимо доказать монотонность функции, на несколько интервалов. Затем на каждом интервале необходимо проанализировать знак производной функции. Если производная положительна на каждом интервале, то функция возрастает. Если производная отрицательна на каждом интервале, то функция убывает. Если же на каждом интервале производная равна нулю, то функция является константной.
- Метод знакопостоянства функции. При использовании этого метода необходимо проанализировать знак самой функции на заданном промежутке. Если функция всегда положительна, то она возрастает. Если функция всегда отрицательна, то она убывает. Если же функция принимает постоянное значение (равно нулю), то она является константной.
Выбор метода доказательства монотонности зависит от конкретной ситуации и предпочтений исследователя. Однако, каждый из этих методов может быть эффективно использован для доказательства монотонности функции и получения более подробной информации о ее поведении на заданном промежутке.
Особенности монотонной функции: влияние на построение графика
Во-первых, график монотонной функции либо строго возрастает на всей своей области определения, либо строго убывает. Это значит, что нет точек, где значение функции остается постоянным или меняется в противоположную сторону.
Кроме того, монотонная функция может иметь различные точки экстремума, такие как максимумы или минимумы. Но в отличие от немонотонных функций, эти точки экстремума будут единственными и располагаться на границах области определения или в точках разрыва функции.
Еще одной особенностью монотонной функции является ее непрерывность. Функция не может иметь разрывов на своей области определения, за исключением разрывов первого рода. Поэтому график монотонной функции всегда будет представлять собой непрерывную кривую.
При построении графика монотонной функции следует учитывать эти особенности. Они помогут представить изменение значений функции на оси координат и выделить ее ключевые точки, такие как точки экстремума или точка перегиба (в случае наличия).
Виды точек перегиба
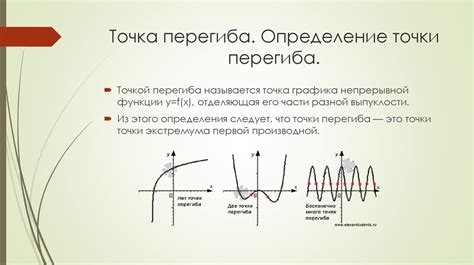
Существует три основных типа точек перегиба:
1. Точки перегиба второго рода
В этих точках график функции меняет свой вогнутый вид на выпуклый или наоборот. Такие точки характеризуются тем, что правая и левая производные функции в этих точках имеют одинаковый знак, а вторая производная функции равна нулю или не определена.
Пример: функция y = x^3 имеет точку перегиба второго рода в точке (0, 0).
2. Точки горизонтального перегиба
В этих точках график функции меняет свой выпуклый или вогнутый вид, однако знаки правой и левой производных функции в этих точках могут различаться. Вторая производная функции в таких точках равна нулю или не определена.
Пример: функция y = x^4 имеет точку горизонтального перегиба в точке (0, 0).
3. Точки перегиба первого рода
В этих точках график функции меняет свой вогнутый вид на выпуклый или наоборот. Правая и левая производные функции в этих точках имеют противоположные знаки, а вторая производная функции равна нулю или не определена.
Пример: функция y = x^2 имеет точку перегиба первого рода в точке (0, 0).








