Взаимно обратные величины являются часто используемым понятием в математике и физике. Они имеют важное значение при решении задач и изучении различных явлений. Взаимно обратные величины представляют собой пару чисел, у которых произведение равно единице.
Определение взаимно обратных величин можно представить следующим образом: если а и b - два числа, и их произведение равно 1, то они называются взаимно обратными. Математически это записывается так: а * b = 1. Например, числа 2 и 1/2 являются взаимно обратными величинами, так как их произведение равно 1.
Пример: пусть имеется линейное уравнение y = 2x. Если для числа x выбрать значение 1/2, то значение y будет равно 1. Это означает, что числа 1/2 и 1 являются взаимно обратными величинами.
Взаимно обратные величины имеют ряд интересных свойств. Во-первых, они обладают свойством симметрии: если а и b - взаимно обратные величины, то и b будет взаимно обратной величиной к а. Во-вторых, взаимно обратные величины являются важными при решении уравнений и задач по пропорциям.
Взаимно обратные числа: что это значит и какие примеры существуют
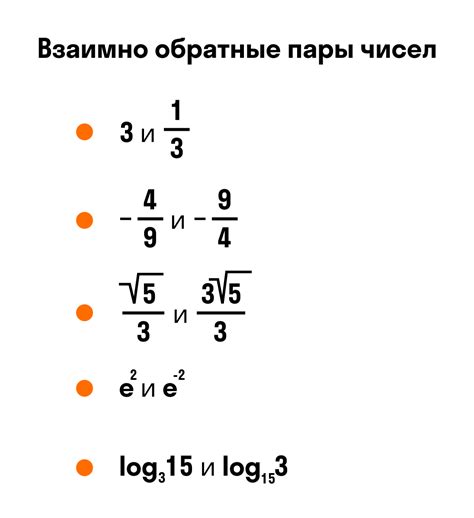
Например, числа 2 и 1/2 являются взаимно обратными, так как 2 * 1/2 = 1. В этой паре 2 - это число, обратное к 1/2, а 1/2 - число, обратное к 2.
Другой пример пары взаимно обратных чисел - это 3 и 1/3. Умножение 3 на 1/3 также дает 1, поэтому они являются взаимно обратными числами. 3 - это число, обратное к 1/3, а 1/3 - число, обратное к 3.
Взаимно обратные числа широко применяются в математике и физике. Они используются, например, для обратных операций, вроде деления или нахождения обратной величины.
Взаимно обратные числа представляют собой важный концепт в математике и используются во множестве областей, где требуется нахождение обратной величины или пропорциональности.
Определение взаимной обратности чисел
В математике два числа называются взаимно обратными, если их произведение равно единице.
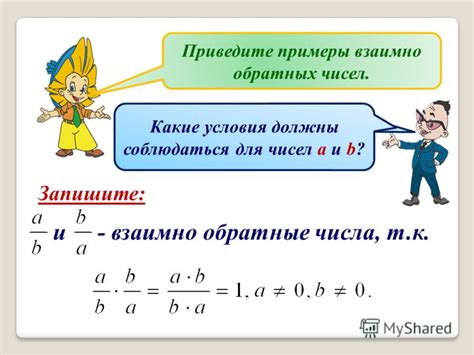
Пусть у нас есть два числа a и b. Тогда они будут взаимно обратными, если выполняется следующее равенство:
a * b = 1
Примером взаимно обратных чисел являются 2 и 1/2. Их произведение равно единице:
2 * 1/2 = 1
Также взаимно обратными числами являются -3 и -1/3:
-3 * -1/3 = 1
Взаимная обратность чисел имеет важное значение в различных областях математики и физики, например, в алгебре и теории вероятностей. Она используется при решении уравнений, определении обратной матрицы и т.д.
Примеры взаимно обратных чисел
Ниже приведены некоторые примеры взаимно обратных чисел:
- 2 и 1/2: 2 * (1/2) = 1
- 3 и 1/3: 3 * (1/3) = 1
- 4 и 1/4: 4 * (1/4) = 1
- 5 и 1/5: 5 * (1/5) = 1
Это лишь некоторые из возможных примеров взаимно обратных чисел. Взаимно обратные числа могут иметь различные значения, но результат их умножения всегда будет равен 1. Это свойство полезно во многих областях математики и физики.
Где взаимно обратные числа используются
Взаимно обратные числа широко применяются в различных областях математики и науки, где требуется обратное преобразование или деление.
Ниже приведены некоторые примеры использования взаимно обратных чисел:
- Дроби: Взаимно обратные числа используются для преобразования дробей взаимно обратные. Например, значение 1/2 является взаимно обратным числу 2, так как их произведение равно 1.
- Проценты: Взаимно обратные числа используются для преобразования процентов в десятичные дроби. Например, 10% эквивалентно десятичной дроби 0,1, что является взаимно обратным числом к 10.
- Физика: Взаимно обратные числа широко применяются в физике, особенно при работе с единицами измерения. Например, между секундами и герцами существует взаимно обратная связь, так как герцы измеряют частоту, то есть количество циклов в секунду.
- Компьютерная графика: Взаимно обратные числа используются для преобразования координат и масштабирования объектов в компьютерной графике. Например, при масштабировании объекта в двухмерном пространстве координаты должны быть преобразованы взаимно обратным числом к коэффициенту масштабирования.
Это лишь некоторые примеры использования взаимно обратных чисел. Изучение и понимание концепции взаимно обратных чисел может быть полезным для понимания различных математических и научных концепций, а также для решения разнообразных задач.
Связь взаимно обратных чисел с алгеброй и физикой

Связь взаимно обратных чисел с алгеброй проявляется в различных уравнениях и задачах. Например, при решении системы уравнений может потребоваться найти значения взаимно обратных переменных. Также в алгебре можно использовать свойства взаимно обратных чисел для упрощения выражений и выполнения различных операций.
В физике взаимно обратные числа также находят применение. Например, в физических законах может возникать необходимость использовать взаимно обратные величины для описания определенных процессов. Кроме этого, взаимно обратные числа могут быть связаны с пропорциональностью между различными физическими величинами.
Поэтому понимание связи взаимно обратных чисел с алгеброй и физикой является важным для понимания и применения соответствующих концепций в этих областях знаний.








