Взаимная тройка векторов является одним из важных понятий линейной алгебры. Это совокупность трех векторов, которые образуют особый набор, нарушающий тривиальное положение в пространстве. Каждый вектор в тройке не может быть линейной комбинацией других двух векторов.
Для классификации взаимных троек векторов используется понятие линейной независимости. Если векторы в тройке являются линейно независимыми, то они образуют базис в пространстве. Другими словами, они способны описать любую точку в пространстве. Если же векторы линейно зависимы, то они находятся в одной плоскости или даже совпадают.
Взаимные тройки векторов активно используются в различных областях науки и техники. Например, в физике они помогают решить задачу о силе и упругости тела, в геометрии и компьютерной графике - для определения координат объектов в трехмерном пространстве.
Рассмотрим пример взаимной тройки векторов. Предположим, у нас есть трое векторов: A(1, 0, 0), B(0, 1, 0) и C(0, 0, 1). Каждый вектор из этой тройки ортогонален другим двум. Такая тройка векторов называется ортонормированной. Она играет фундаментальную роль в линейной алгебре и на практике применяется для решения множества задач.
Взаимная тройка векторов: основные понятия и примеры
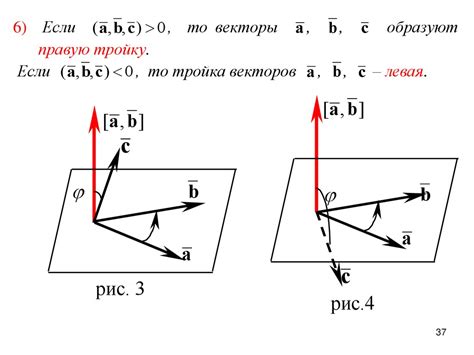
Основными понятиями, связанными с взаимной тройкой векторов, являются коллинеарность, компланарность и линейная зависимость.
Коллинеарность – это свойство трех векторов быть линейно зависимыми. Взаимная тройка векторов называется коллинеарной, если она состоит из векторов, параллельных друг другу или имеющих общее направление.
Компланарность – это свойство трех векторов быть лежащими в одной плоскости. Взаимная тройка векторов называется компланарной, если она лежит в одной плоскости или может быть перенесена в одну плоскость с помощью параллельного переноса.
Линейная зависимость – это свойство трех векторов быть выражаемыми линейной комбинацией других векторов. Взаимная тройка векторов называется линейно зависимой, если существует такая тройка коэффициентов, при которых третий вектор является линейной комбинацией первых двух.
Примером взаимной тройки векторов может служить тройка векторов, определяющая стороны треугольника. Векторы, соединяющие вершины треугольника, будут образовывать компланарную взаимную тройку векторов.
Изучение взаимной тройки векторов позволяет более точно описывать пространственные объекты и их свойства, а также выполнять различные вычисления и преобразования с помощью линейной алгебры.
Определение взаимной тройки векторов
Если векторы a, b и c образуют взаимную тройку, то они должны удовлетворять следующим условиям:
- Векторы не принадлежат одной плоскости, то есть их линейная комбинация не может выразиться через векторы, лежащие в одной плоскости.
- Любая подсистема из двух векторов является линейно независимой, то есть система векторов a и b, a и c, b и c является линейно независимой.
- Любая тройка векторов не может быть представлена как линейная комбинация двух других векторов, то есть нельзя выразить вектор a через b и c, вектор b через a и c или вектор c через a и b.
Взаимные тройки векторов часто используются в физике, геометрии и других областях, где требуется описание трехмерного пространства. Например, взаимная тройка векторов может быть использована для определения положения тела в пространстве, направления сил или векторов скорости.
Основные свойства взаимной тройки векторов

Основные свойства взаимной тройки векторов:
- Линейная независимость: векторы в тройке должны быть линейно независимыми, то есть не могут быть выражены через друг друга с помощью линейных комбинаций.
- Ортогональность: тройка векторов считается ортогональной, если все три вектора в ней взаимно ортогональны между собой.
- Единичность: векторы в тройке могут быть единичными, то есть иметь длину равную единице.
- Правая тройка: векторы в тройке могут быть упорядочены таким образом, что они образуют правую тройку. Это значит, что если мы пронумеруем векторы тройки, то индексы будут идти в порядке против часовой стрелки.
Примеры взаимной тройки векторов:
- Базисные векторы в трехмерном пространстве: i, j, k.
- Векторы основных цветов: red, green, blue.
- Векторы, образующие базис в трехмерном пространстве: {1, 0, 0}, {0, 1, 0}, {0, 0, 1}.
Взаимно перпендикулярные векторы
Взаимно перпендикулярными называются векторы, которые образуют прямые углы между собой. Другими словами, если два вектора перпендикулярны, то их скалярное произведение равно нулю.
Для проверки взаимной перпендикулярности векторов a и b можно использовать следующую формулу:
| a · b = 0 |
|---|
Геометрический смысл взаимно перпендикулярных векторов заключается в том, что они направлены вдоль двух взаимно перпендикулярных осей. Найти примеры взаимно перпендикулярных векторов можно в трехмерном пространстве, например, вектор (1, 0, 0), вектор (0, 1, 0) и вектор (0, 0, 1) будут взаимно перпендикулярными, так как каждый из них направлен вдоль одной из координатных осей x, y, и z.
Коллинеарные векторы
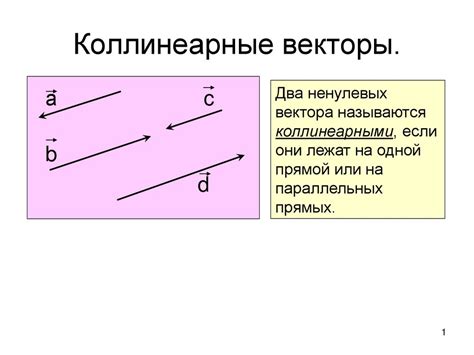
Основная характеристика коллинеарных векторов - пропорциональность. Два вектора являются коллинеарными, если один может быть получен из другого умножением на скалярное значение.
Примеры коллинеарных векторов:
- Вектор (2, 4) и вектор (4, 8) являются коллинеарными, так как второй вектор может быть получен путем умножения первого на 2.
- Вектор (3, 6) и вектор (-3, -6) также являются коллинеарными, так как второй вектор может быть получен путем умножения первого на -1.
Коллинеарные векторы широко используются в геометрии, физике, компьютерной графике и других областях. Знание о коллинеарных векторах позволяет решать задачи связанные с параллельными прямыми, сонаправленными силами, пропорциональными изменениями и многими другими явлениями.
Примеры взаимной тройки векторов в физике
Вот несколько примеров взаимной тройки векторов в физике:
Система сил на неподвижном объекте: рассмотрим случай, когда на неподвижное тело действует три силы. Такие силы могут быть направлены в разные стороны и иметь разные значения, но при этом они должны быть расположены в одной плоскости. Например, можно представить себе ситуацию, когда на неподвижное кубическое тело, лежащее на горизонтальной поверхности, действуют три силы: гравитационная сила, направленная вниз, нормальная сила, направленная вверх, и трение, направленное вдоль поверхности. Эти силы образуют взаимную тройку векторов.
Электромагнитное поле: взаимная тройка векторов также может использоваться для описания магнитного поля в присутствии электрического и магнитного поля. Например, электрическое поле может быть представлено вектором напряженности электрического поля, а магнитное поле - векторами магнитной индукции и направления магнитного поля. Вместе эти векторы образуют взаимную тройку векторов, которая описывает электромагнитное поле.
Координатные системы: взаимная тройка векторов также может использоваться для описания координатных систем. Например, в декартовой системе координат три вектора осей (x, y, z) образуют взаимную тройку векторов, так как они лежат в одной плоскости и удовлетворяют математическим свойствам.
Это только несколько примеров взаимной тройки векторов в физике. Взаимная тройка векторов широко используется в различных областях физики для описания физических явлений и связей между векторами.








