Числа можно представлять в различных форматах, включая десятичную, двоичную, восьмеричную и шестнадцатеричную системы счисления. Часто возникает необходимость в конвертации числа из одной системы счисления в другую. Одним из наиболее часто используемых примеров является поиск десятичного эквивалента числа.
Для нахождения десятичного эквивалента числа необходимо умножить каждую цифру числа на соответствующую степень основания системы счисления, а затем сложить полученные произведения. Например, пусть дано число 101 в двоичной системе счисления. Чтобы найти эквивалент в десятичной системе, мы умножим первую цифру (1) на 2^2 (4), вторую цифру (0) на 2^1 (2) и третью цифру (1) на 2^0 (1), и затем сложим полученные произведения 4 + 0 + 1, что даёт результат 5.
Подобным образом можно найти десятичный эквивалент для числа в восьмеричной или шестнадцатеричной системе счисления. Но в этих случаях необходимо умножать каждую цифру на соответствующую степень основания системы счисления (8 для восьмеричной и 16 для шестнадцатеричной). Например, число 27 в восьмеричной системе счисления можно преобразовать в десятичный вид, умножив первую цифру (2) на 8^1 (8) и вторую цифру (7) на 8^0 (1), и затем сложив полученные произведения 16 + 7, что даёт результат 23.
Концепция десятичных эквивалентов чисел

Десятичные эквиваленты чисел представляют собой записи чисел в десятичной системе счисления, которая основывается на десяти символах: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Каждая позиция числа имеет определенную весовую стоимость, которая зависит от ее расположения.
В десятичной системе счисления, каждая цифра имеет место в числе в зависимости от ее значения и ее позиции. Например, в числе 123, цифра 1 находится в позиции с весом 100 (10 в степени 2), цифра 2 находится в позиции с весом 10 (10 в степени 1) и цифра 3 находится в позиции с весом 1 (10 в степени 0).
Чтобы найти десятичный эквивалент числа, необходимо умножить каждую цифру числа на соответствующую ее весовой стоимости и сложить полученные произведения. Таким образом, для числа 123 десятичным эквивалентом будет 1 * 100 + 2 * 10 + 3 * 1 = 123.
Понимание концепции десятичных эквивалентов чисел важно для работы с десятичными числами и применяется в множестве вычислительных задач, а также в повседневной жизни.
Что такое десятичные эквиваленты чисел?
Числа в десятичной системе записываются с использованием десяти разрядов (от 0 до 9) и позиционной системы. Значение каждого разряда определяется его позицией относительно точки разделителя. Целые числа находятся слева от точки, а десятичные числа - справа.
Например, число 25 в десятичной системе обозначает 2 десятка и 5 единиц, записывается как 25. Десятичное число 3.14 означает 3 целых и 14 сотых, записывается как 3.14.
Для некоторых чисел, особенно дробей и процентов, может быть полезно найти их десятичные эквиваленты. Десятичное представление позволяет сравнивать, складывать и вычитать такие числа более удобным образом.
Найти десятичные эквиваленты чисел можно с помощью различных методов, включая деление в столбик, использование калькулятора или математических формул.
Знание десятичных эквивалентов чисел важно для решения задач в различных областях, таких как финансы, наука, инженерия и торговля. Оно помогает точно представить значения и сравнивать числа для принятия обоснованных решений.
Как найти десятичные эквиваленты чисел

Десятичные эквиваленты чисел представляют собой десятичные дроби или числа в десятичной системе счисления, которые имеют тот же математический смысл, что и исходные числа в других системах счисления. Нахождение десятичных эквивалентов может быть полезно во многих областях, включая математику, физику и программирование.
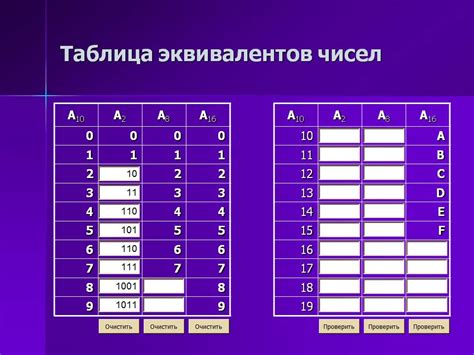
Существует несколько способов нахождения десятичных эквивалентов чисел. Один из них - использование таблицы соответствия. Для этого составляется таблица, где в первом столбце записываются исходные числа, а во втором столбце - их десятичные эквиваленты. Затем, в соответствии с правилами системы счисления, каждое число в первом столбце преобразуется в десятичное число и записывается во втором столбце.
| Исходное число | Десятичный эквивалент |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
Другим способом нахождения десятичных эквивалентов является использование математической формулы. Для чисел в десятичной системе счисления формула имеет простую структуру: каждая цифра числа умножается на 10 в степени, равной её положению в числе минус 1, и затем результаты суммируются.
Например, для числа 345 формула будет выглядеть так:
(3 * 10^2) + (4 * 10^1) + (5 * 10^0) = 300 + 40 + 5 = 345
Таким образом, десятичный эквивалент числа 345 равен 345.
Нахождение десятичных эквивалентов чисел может быть полезным при выполнении различных вычислений или преобразований чисел из одной системы счисления в другую. Определение десятичных эквивалентов помогает лучше понять и работать с числами в контексте десятичной системы счисления.
Методы поиска десятичных эквивалентов чисел
Существует несколько методов, которые можно использовать для поиска десятичных эквивалентов чисел. Каждый из этих методов имеет свои особенности и может быть полезен в разных ситуациях.
1. Деление числа на 10 в степени n:
Для поиска десятичного эквивалента числа можно разделить его на 10, возведенное в нужную степень n. Например, если нужно найти десятичный эквивалент числа 25 в десятичной системе счисления, можно разделить 25 на 10 в степени 2 (так как в десятичной системе счисления позиции цифр увеличиваются в 10 раз с каждой следующей позицией).
Для этого нужно выполнить следующие шаги:
- Разделить число на 10, возведенное в степень n.
- Округлить полученное значение до нужной точности (обычно до определенного количества знаков после запятой).
- Полученное значение будет являться десятичным эквивалентом исходного числа.
2. Использование таблицы десятичных эквивалентов:
Для некоторых чисел, таких как десятичные доли или обыкновенные дроби, можно использовать специальные таблицы десятичных эквивалентов. В этих таблицах указано, какие числа соответствуют определенным десятичным дробям или долям.
Чтобы найти десятичный эквивалент числа с помощью таблицы, нужно найти соответствующую десятичную дробь или долю в таблице и использовать ее значение.
3. Использование калькулятора:
Если у вас есть доступ к калькулятору, его можно использовать для поиска десятичного эквивалента числа. В большинстве калькуляторов есть функция, которая позволяет переводить числа из одной системы счисления в другую. Нужно только ввести исходное число и выбрать десятичную систему счисления. Калькулятор автоматически найдет десятичный эквивалент.
Эти методы могут быть полезны при работе с числами и переводе их из одной системы счисления в другую. Важно помнить, что точность десятичного эквивалента зависит от выбранного метода и заданной точности округления.
Практические примеры использования десятичных эквивалентов чисел
Десятичные эквиваленты чисел могут быть полезными при выполнении различных математических операций, а также при преобразовании чисел из одной системы счисления в другую. Рассмотрим несколько примеров, иллюстрирующих практическое использование десятичных эквивалентов чисел.
Пример 1: Вычисление процентов.
Предположим, у нас есть число 50, и мы хотим найти 15% от этого числа. Для этого мы можем использовать десятичный эквивалент процента, который равен 0,15. Умножим число 50 на 0,15 и получим результат 7,5. Таким образом, 15% от числа 50 равно 7,5.
| Исходное число | Процент | Результат |
|---|---|---|
| 50 | 15% | 7,5 |
Пример 2: Преобразование числа из одной системы счисления в другую.
Предположим, у нас есть число 101110 в двоичной системе счисления, и мы хотим преобразовать его в десятичное число. Чтобы это сделать, мы можем использовать десятичные эквиваленты цифр в двоичной системе. Каждой цифре в двоичном числе присваивается десятичный эквивалент, который соответствует позиции цифры в числе. Таким образом, число 101110 в двоичной системе счисления эквивалентно числу 46 в десятичной системе счисления.
| Двоичное число | Десятичное число |
|---|---|
| 101110 | 46 |
Пример 3: Вычисление длины окружности.
Предположим, у нас есть окружность с радиусом 5 см, и мы хотим найти её длину. Для этого мы можем использовать десятичный эквивалент числа Пи, который примерно равен 3,14159. Формула для вычисления длины окружности: длина = 2 * Пи * радиус. Подставим значение радиуса в формулу и получим ответ: длина окружности равна примерно 31,4159 см.
| Радиус окружности (см) | Число Пи | Длина окружности (см) |
|---|---|---|
| 5 | 3,14159 | 31,4159 |
Это всего лишь несколько примеров, демонстрирующих практическое использование десятичных эквивалентов чисел. Понимание и использование этих концепций поможет вам решать различные математические задачи и преобразовывать числа в разные системы счисления.








