В геометрии окружность – это кривая линия, состоящая из всех точек плоскости, которые находятся на одинаковом расстоянии от фиксированной точки, называемой центром окружности. Когда говорят, что окружность "вписана" в другую фигуру, это значит, что окружность полностью находится внутри данной фигуры и касается её всех сторон.
Внутренняя окружность, которая касается всех сторон многоугольника, называется «вписанной окружностью» или «окружностью вписанной в многоугольник». Впиcанная окружность основана на особом свойстве равнобедренного треугольника, в который вписана данная окружность. Центр этой окружности совпадает с точкой пересечения биссектрис.
Вписанная окружность обладает рядом важных свойств. Во-первых, она делит стороны многоугольника на равные или пропорциональные части. Во-вторых, касательные к вписанной окружности, проведенные в точках касания, делят все радиусы на равные или пропорциональные отрезки.
Интересно отметить, что радиус вписанной окружности является геометрическим центром данного многоугольника. Также, диаметр вписанной окружности будет равен стороне многоугольника, на которую он опирается.
Ввиду своих свойств, вписанная окружность имеет много применений в геометрии. Она используется при решении задач на нахождение площади и периметра многоугольника, а также при вычислении различных углов и длин отрезков внутри многоугольника.
Определение понятия "вписана окружность"
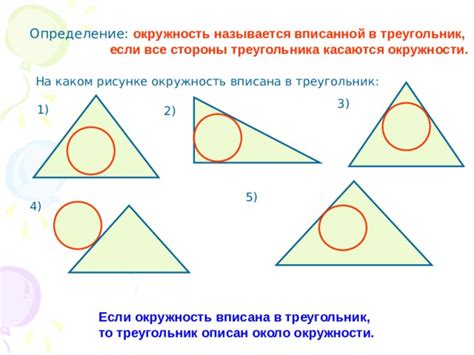
Одно из наиболее известных свойств вписанной окружности - это то, что центр окружности лежит в точке пересечения биссектрис всех углов многоугольника, ограничивающего окружность.
Вписанная окружность имеет ряд важных свойств и применений в геометрии. Например, она используется для решения задачи по построению многоугольника по заданным сторонам, а также для нахождения площади многоугольника и его периметра.
Кроме того, вписанная окружность имеет много связей с другими фигурами и окружностями. Например, для любой вписанной окружности существует описанная окружность, которая касается всех сторон многоугольника и имеет центр в той же точке.
Свойства вписанной окружности
- Центр вписанной окружности лежит на перпендикулярах, проведенных из середин сторон многоугольника.
- Радиус вписанной окружности равен половине длины диагонали вписанного многоугольника.
- Точки касания окружности со сторонами многоугольника делят эти стороны на отрезки, равные друг другу.
- Углы, образованные сторонами многоугольника и радиусами вписанной окружности, имеют равную величину.
- Сумма всех углов, образованных сторонами многоугольника и радиусами вписанной окружности, равна сумме углов многоугольника.
Важно отметить, что вписанная окружность существует только для многоугольников, имеющих хотя бы три стороны.
Как найти центр вписанной окружности

- Проведите биссектрису каждого угла треугольника. Биссектриса каждого угла делит его на два равных угла.
- Найдите точку пересечения биссектрис. Эта точка является центром вписанной окружности.
- Проведите окружность, используя найденный центр и любую из вершин треугольника.
Теперь вы знаете, как найти центр вписанной окружности треугольника. Зная центр, вы можете определить радиус и длину дуги этой окружности.
Теорема о вписанной окружности
В треугольнике с центром в ортоцентре, сторона которого представлена линиями, проходящими через основания высот треугольника, вписанная окружность касается каждой из его сторон.
То есть, если провести перпендикулярные линии от центра окружности к сторонам треугольника, они будут касаться этих сторон в одной точке.
 | На рисунке изображен треугольник со сторонами a, b и c, а также вписанная окружность с радиусом r и центром O. Точки касания окружности с сторонами обозначены как A', B' и C'. Согласно теореме о вписанной окружности, отрезки OA', OB' и OC' равны по длине: OA' = OB' = OC' = r. Это означает, что радиус вписанной окружности равен расстоянию от центра окружности до точки касания с любой из сторон треугольника. |
Теорема о вписанной окружности имеет множество следствий и применений в геометрии. Она позволяет, например, находить радиус вписанной окружности по длинам сторон треугольника и наоборот, находить длины сторон треугольника по радиусу вписанной окружности.
Важно отметить, что теорема о вписанной окружности верна только для треугольников, в которых радиус окружности не равен нулю. Если радиус равен нулю, то исключительным случаем будет точка вместо окружности, которая будет касаться всех сторон треугольника. В этом случае треугольник называется ортоцентрическим.
Как найти радиус вписанной окружности
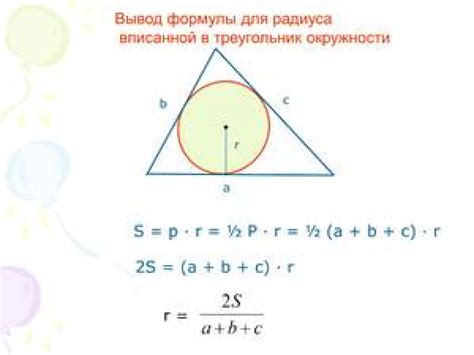
Существует несколько способов определения радиуса вписанной окружности:
- По длинам сторон треугольника: радиус вписанной окружности может быть найден с помощью формулы r = (a + b + c) / (2p), где a, b и c - длины сторон треугольника, а p - полупериметр треугольника.
- По площади треугольника: радиус вписанной окружности можно выразить через площадь треугольника по формуле r = P / p, где P - площадь треугольника, а p - полупериметр треугольника.
- С помощью формулы герона: если известны длины сторон треугольника и его площадь, то радиус вписанной окружности можно найти по формуле r = sqrt((P / p) * (p - a) * (p - b) * (p - c)), где P - площадь треугольника, a, b и c - длины сторон треугольника, а p - полупериметр треугольника.
Зная радиус вписанной окружности, можно определить и другие свойства данной окружности, такие как длина окружности и площадь круга, описанного около треугольника.
Если треугольник равносторонний, то радиус вписанной окружности равен трети его высоты.
Таким образом, нахождение радиуса вписанной окружности является важным шагом при изучении геометрии и решении задач, связанных с треугольниками.
Связь вписанной окружности и треугольника
Одно из свойств вписанной окружности заключается в том, что точка пересечения биссектрис треугольника является центром вписанной окружности. Биссектрисой называется линия, которая делит угол треугольника на два равных угла. Это свойство позволяет легко найти центр вписанной окружности, если известны биссектрисы треугольника.
Другое свойство вписанной окружности связано с касательными, проведенными из вершин треугольника. Если из точек пересечения касательных с вписанной окружностью провести отрезки до центра окружности, то эти отрезки будут равны. Таким образом, длина отрезка, проведенного от вершины треугольника до центра вписанной окружности, равна радиусу окружности.
Вписанная окружность также связана со сторонами треугольника. Точки касания окружности со сторонами треугольника делят эти стороны на отрезки, которые являются взаимно пропорциональными. Это значит, что отношение длин двух смежных отрезков, образованных точками касания окружности со сторонами треугольника, равно отношению длин других двух смежных отрезков.
Свойства вписанной окружности и треугольника позволяют решать различные задачи и находить дополнительные связи между элементами треугольника. Эти свойства являются важными для геометрии и находят применение в различных областях, например, в построении и анализе треугольников.
Применение вписанной окружности

Вписанная окружность часто применяется в геометрии и математике для решения различных задач.
Одним из применений вписанной окружности является вычисление площади многоугольника. Если известны радиус вписанной окружности и количество сторон многоугольника, то площадь многоугольника можно вычислить по формуле:
S = (n * r^2 * sin(2π/n)) / 2,
где S - площадь многоугольника, n - количество сторон многоугольника, r - радиус вписанной окружности.
Вписанная окружность также используется для нахождения длин сторон многоугольника. Если известны радиус вписанной окружности и угол между сторонами многоугольника, то длина стороны многоугольника может быть вычислена по формуле:
a = 2 * r * sin(π/n),
где a - длина стороны многоугольника, n - количество сторон многоугольника, r - радиус вписанной окружности.
Окружность, вписанная в треугольник, также имеет применение в тригонометрии. С помощью радиуса вписанной окружности можно выразить площадь треугольника через синус углов. Для треугольника с радиусом вписанной окружности r и углами A, B и C, площадь можно выразить следующей формулой:
S = r^2 * (sin(A) + sin(B) + sin(C))/2.
Вписанная окружность также имеет важное значениe при решении задач, связанных с пересечением окружностей, касательной к окружности и других геометрических построений. Она помогает упростить расчеты и связать различные параметры фигур в геометрических задачах.








