Сумма координат точки является одним из основных понятий в математике и геометрии. Координаты точки в двумерном пространстве представляют собой числовые значения, которые определяют положение точки относительно начала координат.
Сумма координат точки может быть вычислена путем сложения вертикальной (y) и горизонтальной (x) координат. Для точки с координатами (x, y) сумма координат будет равна x + y. Например, если точка имеет координаты (3, 4), то сумма координат будет равна 3 + 4 = 7.
Сумма координат точки может быть полезна во многих областях, включая физику, информатику и географию. Она позволяет определить положение точки относительно другой точки или относительно осей координат. Кроме того, сумма координат может быть использована для решения задач на нахождение периметра фигуры или расстояния между точками.
Определение суммы координат точки
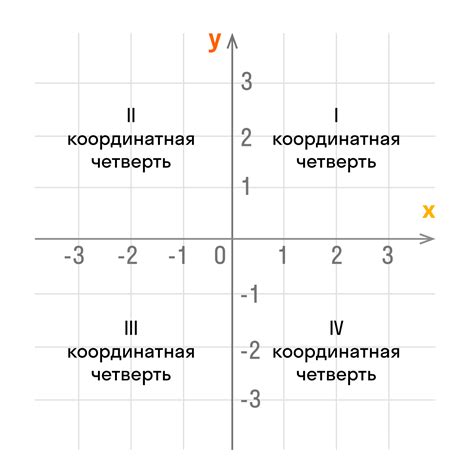
Для нахождения суммы координат точки необходимо сложить значения ее абсциссы и ординаты. Например, если координаты точки равны (2, 3), то сумма координат будет равна 2 + 3 = 5.
Сумма координат может использоваться в различных математических и геометрических задачах. Например, для определения центра масс системы точек или для нахождения среднего значения между двумя точками.
Определение суммы координат точки является простым и основным понятием в математике и геометрии, и является базой для более сложных операций и концепций.
Векторы и координаты
Когда мы говорим о векторах в координатном пространстве, мы обычно говорим о векторах, заданных в виде координат. Координаты точки представляют собой числа, которые определяют положение точки относительно начала координатной системы.
Например, в двумерной плоскости точка может быть задана парой чисел (x, y), где x - это координата точки по оси x, а y - координата точки по оси y. В трехмерном пространстве точка может быть задана тройкой чисел (x, y, z), где x, y и z - это координаты точки по осям x, y и z соответственно.
Итак, сумма координат точки - это сумма всех координат этой точки. Например, если у нас есть точка (x, y) в двумерной плоскости, то ее сумма координат будет равна x + y.
Вычислить сумму координат точки очень просто - достаточно сложить все числа-координаты, которые задают точку. Например, для точки (3, 5, 2) в трехмерном пространстве, сумма координат будет равна 3 + 5 + 2 = 10.
Сумма координат точки имеет важное значение при решении многих задач в геометрии и физике. Например, она может использоваться для вычисления расстояния между двумя точками, определения вектора между двумя точками и других задач.
Как вычислить сумму координат
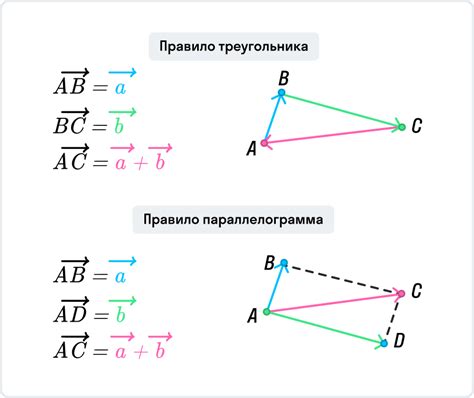
Для вычисления суммы координат точки следует сложить каждую соответствующую координату точки. Например, для двумерного пространства с координатами (x, y), сумма координат будет x + y.
Пример вычисления суммы координат для точки P с координатами (3, 5) в двумерном пространстве:
Сумма координат = 3 + 5 = 8.
Таким образом, сумма координат точки P равна 8.
Вычисление суммы координат может быть полезно при работе с графиками, координатными плоскостями и другими задачами, связанными с пространственным представлением данных.
Координатная плоскость
Одна ось, обычно называемая горизонтальной или осью абсцисс, обозначается буквой "x". Вторая ось, обычно называемая вертикальной или осью ординат, обозначается буквой "y". Точка на координатной плоскости задается парой чисел (x, y), где x - координата по оси абсцисс, а y - координата по оси ординат.
Сумма координат точки на координатной плоскости представляет собой алгебраическую сумму ее координат по осям абсцисс и ординат. Для точки с координатами (x, y) сумма координат будет равна x + y.
Вычислить сумму координат точки на координатной плоскости очень просто. Для этого нужно сложить значение координаты по оси абсцисс (x) с значением координаты по оси ординат (y). Полученная сумма будет являться суммой координат данной точки.
Координатная плоскость широко используется в различных областях, таких как математика, физика, инженерия, компьютерная графика и др. Она позволяет удобно визуализировать и анализировать различные геометрические объекты, а также решать различные задачи, связанные с расчетами и измерениями.
| Ось координат | Направление | Обозначение |
|---|---|---|
| Абсцисса (x-ось) | Горизонтально, слева направо | x |
| Ордината (y-ось) | Вертикально, снизу вверх | y |
Декартова система координат
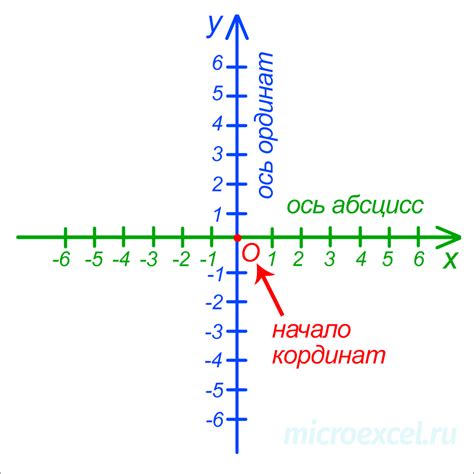
В двумерной декартовой системе координат точка задается двумя числами, обозначающими разницу между ее положением и некоторой фиксированной точкой, называемой началом координат. Первое число обозначает расстояние точки по оси X, а второе число - по оси Y.
Например, точка (2, 3) означает, что она находится на два единичных отрезка вправо от начала координат и на три единичных отрезка вверх.
Сумма координат точки в двумерной декартовой системе равна сумме ее значения по оси X и значения по оси Y. Например, для точки (2, 3) сумма координат будет равна 2 + 3 = 5.
В трехмерной декартовой системе координат точка задается тремя числами, обозначающими разницу между ее положением и началом координат вдоль осей X, Y и Z. Сумма координат точки в трехмерной системе равна сумме ее значения по оси X, значения по оси Y и значения по оси Z.
Декартова система координат используется в различных областях, таких как математика, физика, геометрия, компьютерная графика и многих других.








