Равнобедренная трапеция - это четырехугольник, у которого две стороны параллельны, а другие две равны друг другу. Особенностью этой фигуры является то, что углы при основании равны, а диагонали равны между собой. Равнобедренная трапеция получила свое название из-за своей схожести с равнобедренным треугольником.
Свойства равнобедренной трапеции значительно облегчают решение задач, связанных с ее геометрией. Например, если у трапеции одно из оснований является высотой, то другая сторона будет равна основанию. Это свойство позволяет легко находить значение неизвестной стороны или угла.
Примеры равнобедренных трапеций можно встретить не только в геометрических задачах, но и в реальной жизни. Например, форма затонувшего корабля, крыша дома или даже форма некоторых пирамид имеют сходство с равнобедренной трапецией.
Изучение равнобедренных трапеций является важным аспектом геометрии, а их свойства и применение широко применяются в различных областях науки и техники. Знание этих свойств позволяет решать задачи по определению площадей, нахождению высоты, углов и диагоналей трапеции. Поэтому, изучение равнобедренных трапеций является неотъемлемой частью геометрии и имеет практическую ценность в реальной жизни.
Равнобедренная трапеция - что это?
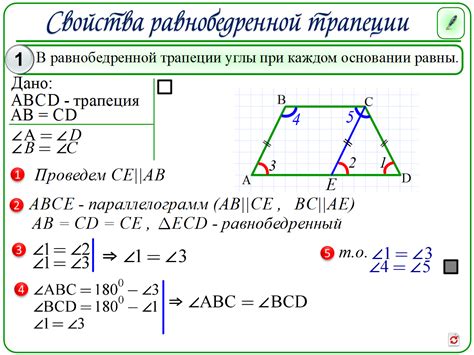
Основание равнобедренной трапеции - это пара параллельных сторон, а высота - перпендикуляр, опущенный из вершины равнобедренной трапеции на основание. Также в равнобедренной трапеции углы при основаниях являются равными.
Свойства равнобедренной трапеции:
- У равнобедренной трапеции стороны оснований параллельны.
- У равнобедренной трапеции углы при основаниях равны.
- У равнобедренной трапеции боковые стороны равны.
- Высота, опущенная из вершины на основание, равна серединному перпендикуляру, находящемуся между двумя основаниями.
Примеры равнобедренных трапеций: трапеции с равными боковыми сторонами и равными углами при основаниях. Также множество фигур, таких как пирамиды или здания, могут иметь форму равнобедренной трапеции.
Основные свойства равнобедренной трапеции
1. Боковые стороны равны между собой. Это значит, что отрезки, соединяющие вершины трапеции с противоположными сторонами, имеют одинаковую длину.
2. Боковые углы равны между собой. Это означает, что углы, образованные боковыми сторонами и основаниями трапеции, имеют одинаковую величину.
3. Диагонали пересекаются в точке, делящей их пополам. Это значит, что отрезок, соединяющий середины диагоналей, является высотой трапеции и делит ее на два равных треугольника.
4. Сумма углов трапеции равна 360 градусов. Это свойство является общим для всех многоугольников.
5. Высота равнобедренной трапеции является средним геометрическим длин основания и основания-катета. Если обозначить высоту как h, основание как a, и основание-катет как b, то можно записать следующую формулу: h = √(a*b).
Эти свойства равнобедренной трапеции помогают установить их особенности и применение в различных задачах геометрии.
Формула для вычисления площади равнобедренной трапеции

Площадь равнобедренной трапеции может быть вычислена с помощью специальной формулы. Для этого необходимо знать длину оснований и высоты трапеции.
Формула для вычисления площади равнобедренной трапеции:
- Пусть основание трапеции, которая расположена выше, равно a.
- Пусть основание трапеции, которая расположена ниже, равно b.
- Пусть высота трапеции равна h.
Тогда площадь равнобедренной трапеции вычисляется по формуле:
Площадь = (a + b) * h / 2
Например, если основания равнобедренной трапеции равны 6 см и 10 см, а высота равна 4 см, то площадь трапеции будет:
Площадь = (6 см + 10 см) * 4 см / 2 = 16 см²
Таким образом, площадь равнобедренной трапеции составляет 16 квадратных сантиметров.
Как найти периметр равнобедренной трапеции?
Для нахождения периметра равнобедренной трапеции нужно:
- Найти длины всех сторон. Обозначим эти стороны следующим образом: основание трапеции – a, основание трапеции – b, боковые стороны трапеции – c и d.
- Применить формулу для нахождения периметра: П = a + b + c + d.
Пример:
Допустим, что у нас есть равнобедренная трапеция, у которой длина основания a равна 5 см, длина основания b равна 8 см, а длины боковых сторон c и d равны 10 см каждая.
Чтобы найти периметр этой трапеции, нужно применить формулу: П = 5 + 8 + 10 + 10 = 33 см.
Таким образом, периметр равнобедренной трапеции в данном примере равен 33 см.
Примеры равнобедренных трапеций в жизни

Равнобедренные трапеции встречаются в разных сферах нашей жизни и имеют практическое применение. Вот некоторые примеры:
1. Архитектура
В архитектуре равнобедренные трапеции часто используются в строительстве зданий. Например, крыша, имеющая форму равнобедренной трапеции, обеспечивает лучшую стабильность и прочность здания.
2. Автомобильные шины
Шины на автомобилях также могут иметь форму равнобедренной трапеции. Это делается для улучшения сцепления с дорогой и повышения безопасности на дороге.
3. Габаритные отсеки
В транспорте, например в поездах или самолетах, габаритные отсеки могут иметь форму равнобедренной трапеции. Это позволяет эффективно использовать пространство и размещать грузы.
4. Искусство и дизайн
В дизайне и искусстве равнобедренные трапеции могут использоваться для создания эстетически приятных композиций и образов. Например, в архитектуре или в декорировании интерьера.
5. Геометрия и математика
Само собой разумеется, равнобедренные трапеции широко используются в области геометрии и математики. Они являются объектом изучения и используются для решения задач и различных математических вычислений.
Таким образом, равнобедренные трапеции находят свое применение в разных сферах нашей жизни и имеют практическую значимость.








