Произвольный отрезок – это часть прямой, ограниченная двумя точками. В геометрии отрезок является одним из основных понятий и широко используется для изучения пространства и расстояний между объектами. Отрезок имеет начальную и конечную точки, которые определяют его длину и положение на прямой.
Для задания произвольного отрезка обычно используются две точки. Например, отрезок AB обозначает промежуток между точкой A и точкой B. Отрезок может быть вертикальным, горизонтальным или наклонным в зависимости от положения его начальной и конечной точек.
Важно отметить, что отрезок включает в себя все точки, находящиеся между его начальной и конечной точками. Таким образом, если отрезок AB – это отрезок, который включает точки A и B, то отрезок BA – это тот же самый отрезок, но с другим направлением.
Произвольные отрезки находят широкое применение в различных областях науки и техники. Например, в физике отрезки используются для измерения расстояния и времени, в графике и дизайне – для строительства геометрических фигур и формирования пропорций, а в программировании – для описания отрезков на числовой оси.
Определение произвольного отрезка
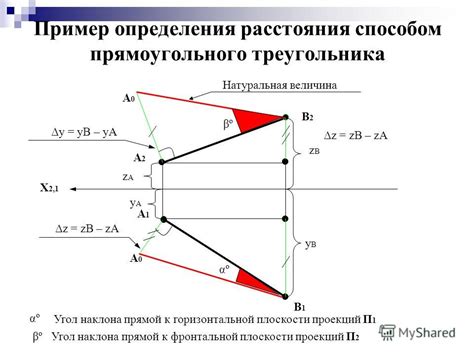
Произвольным отрезком называется часть прямой, ограниченная двумя точками, которые называются концами отрезка. Концы отрезка принадлежат самому отрезку, а все остальные точки этой прямой, кроме концов, не принадлежат отрезку.
Примеры произвольных отрезков:
- Отрезок AB, где A и B - две различные точки на прямой.
- Отрезок CD, где C и D - точки, расположенные не на одной прямой.
- Отрезок EF, где E и F - точки, совпадающие друг с другом.
Произвольные отрезки могут быть разной длины, включать или не включать свои концы, а также быть расположенными в разных направлениях на прямой.
Определение и основные характеристики
Основные характеристики произвольного отрезка:
- Начальная точка: первая точка, которая ограничивает отрезок с одной стороны. Принято обозначать ее как A.
- Конечная точка: вторая точка, которая ограничивает отрезок с другой стороны. Принято обозначать ее как B.
- Длина: расстояние между начальной и конечной точками отрезка. Часто обозначается как AB или |AB|.
- Прямая: отрезок является частью прямой линии, которая продолжается в обе стороны за пределами отрезка.
- Непрерывность: отрезок не имеет разрывов или пропусков, он состоит из всех точек между начальной и конечной точками.
Произвольные отрезки широко используются в геометрии, анализе и других областях математики для измерения расстояний, построения графиков, моделирования и других задач.
Примеры использования в математике

1. Геометрия
В геометрии произвольные отрезки часто используются для построения фигур и определения их свойств. Например, при решении задач на нахождение площади или периметра прямоугольника, можно взять произвольный отрезок в качестве стороны прямоугольника и использовать его длину в дальнейших расчетах.
2. Аналитическая геометрия
В аналитической геометрии произвольные отрезки используются для задания координатных осей и определения координат точек на плоскости. Например, при построении графика функции можно взять произвольный отрезок на оси абсцисс и отложить на нем значения аргумента функции.
3. Математический анализ
В математическом анализе произвольные отрезки широко используются при рассмотрении пределов и производных функций. Например, при нахождении предела функции или производной, можно взять произвольный отрезок на оси абсцисс, содержащий точку, в которой требуется найти предел или производную.
Таким образом, произвольные отрезки играют важную роль в различных математических разделах, позволяя задавать и исследовать различные параметры и свойства фигур, функций и математических объектов.
Примеры использования в физике
Произвольные отрезки широко используются в физике для моделирования и анализа различных явлений. Вот несколько примеров:
- Движение тела. При изучении движения тела по прямой в физике используется понятие произвольного отрезка. Например, для анализа положения тела в разные моменты времени, можно выбрать произвольный отрезок на оси координат и изучать перемещение тела от одного конца отрезка к другому.
- Сила. При рассмотрении взаимодействия тел в физике, возникает понятие приложения силы в произвольной точке. Например, для определения момента силы относительно данной точки, используют произвольный отрезок, на котором расположена точка приложения силы.
- Электрические цепи. При моделировании и анализе электрических цепей, произвольные отрезки используются для определения сопротивления участков цепи. Например, для расчета силы тока на произвольном участке цепи, можно взять произвольный отрезок данного участка и анализировать его свойства.
Это лишь некоторые примеры использования произвольных отрезков в физике. В дальнейшем, при изучении конкретных разделов физики, произвольные отрезки могут использоваться для решения различных задач и анализа различных явлений.
Примеры использования в программировании

Произвольные отрезки часто используются в программировании для работы с графикой, геометрическими расчетами и визуализацией данных. Вот несколько примеров:
| Язык программирования | Пример использования |
|---|---|
| Python | import matplotlib.pyplot as plt
# Создание произвольного отрезка
x = [1, 2, 3, 4]
y = [1, 4, 9, 16]
# Построение графика
plt.plot(x, y)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('График произвольного отрезка')
plt.show() |
| JavaScript | // Создание произвольного отрезка
var line = document.createElement('div');
line.style.width = '200px';
line.style.height = '4px';
line.style.background = 'black';
// Добавление отрезка на страницу
document.body.appendChild(line); |
| C++ | #include |
Это лишь некоторые примеры использования произвольных отрезков в программировании. Их гибкость и универсальность делают их полезными инструментами в различных областях разработки программного обеспечения.
Роль произвольного отрезка в геометрии
Произвольные отрезки играют важную роль в различных геометрических задачах. Они используются для измерения расстояния между точками и определения положения объектов в пространстве. Например, в треугольнике произвольные отрезки могут служить основанием или высотой, что позволяет находить его площадь и периметр.
Также произвольные отрезки использованы при построении различных фигур, таких как окружность, эллипс или многоугольник. Они помогают определить форму и размеры фигуры, а также провести необходимые геометрические операции.
Кроме того, произвольные отрезки широко применяются в аналитической геометрии и математическом анализе. Они являются основой для определения функций, уравнений и графиков, которые описывают геометрические объекты и их свойства.
Все эти примеры демонстрируют важность произвольных отрезков в геометрии и их неотъемлемую роль в решении геометрических задач.
Примеры задач с использованием произвольных отрезков
Произвольные отрезки широко используются в различных математических задачах. Рассмотрим несколько примеров:
Пример 1:
Даны произвольные отрезки AB и CD на прямой. Найдите точку пересечения этих отрезков.
Пример 2:
В треугольнике ABC даны произвольные отрезки AE и CF, параллельные сторонам треугольника. Найдите точку пересечения этих отрезков.
Пример 3:
Даны произвольные отрезки AB и CD в пространстве. Найдите угол между этими отрезками.
Пример 4:
Даны произвольные отрезки AB и CD на плоскости. Найдите длину отрезка, соединяющего середины этих отрезков.
В каждом из этих примеров произвольные отрезки используются для решения конкретных задач. Они позволяют находить точки пересечения, углы между отрезками, длины отрезков и решать другие геометрические задачи.
Произвольные отрезки в алгоритмах
В алгоритмах произвольные отрезки часто используются для ограничения области поиска или анализа данных. Например, при решении задачи нахождения наибольшего числа в массиве, можно использовать произвольный отрезок, чтобы ограничить поиск только определенной частью массива.
Примером задачи, где используются произвольные отрезки, может быть задача нахождения максимальной суммы подотрезка в массиве. В этом случае, мы можем определить начало и конец произвольного отрезка в массиве и найти сумму элементов этого отрезка. Затем, среди всех возможных отрезков выбрать тот, сумма элементов которого будет максимальной.
Произвольные отрезки также могут использоваться для разбиения данных на несколько частей, например, при параллельной обработке или распределенных вычислениях. В этом случае, каждая часть данных будет обрабатываться отдельно, а результаты будут объединены в конце.
Использование произвольных отрезков в алгоритмах позволяет более гибко и эффективно решать различные задачи, учитывая особенности данных или условия, на которых они основаны.








