Дифференцирование функции – это одно из основных понятий математического анализа, которое позволяет найти производную данной функции. Производная функции, в свою очередь, характеризует скорость изменения значения функции в каждой точке ее области определения. Процесс дифференцирования играет важную роль в решении широкого круга задач и находит применение в различных научных и инженерных областях.
Продифференцировать функцию означает найти ее производную при помощи определенных правил и формул. Обычно это делается с целью нахождения точного значения производной функции, характеризующей изменение функции в конкретной точке или интервале. Производная позволяет найти касательную к кривой графика функции, определить экстремумы функции, понять, в каких точках меняется знак функции и многое другое.
Примеры дифференцирования функцийДля более наглядного представления процесса дифференцирования, рассмотрим примеры простых функций и их производных:
1. Линейная функция
Пусть дана линейная функция f(x) = kx + b, где k и b – заданные константы. Для нахождения производной этой функции нужно применить правило дифференцирования линейной функции: производная линейной функции равна коэффициенту при переменной x. Таким образом, производная функции f(x) будет равна k.
2. Квадратичная функция
Рассмотрим квадратичную функцию f(x) = ax^2 + bx + c, где a, b и c – заданные константы. Для нахождения производной этой функции используется правило дифференцирования квадратичной функции: производная квадратичной функции равна удвоенному значению коэффициента a, умноженному на переменную x, плюс производная линейной функции b. То есть производная функции f(x) будет равна 2ax + b.
Что такое дифференцирование функции и как оно работает?
Дифференцирование осуществляется путем взятия предела отношения приращения функции к приращению аргумента на бесконечно малом интервале. Полученная производная может быть положительной, отрицательной или равной нулю, в зависимости от изменения функции в данной точке.
Производная функции может интерпретироваться как скорость изменения значения функции относительно аргумента. Если производная положительна, функция возрастает; если производная отрицательна, функция убывает; если производная равна нулю, то функция имеет экстремум в данной точке.
Пример:
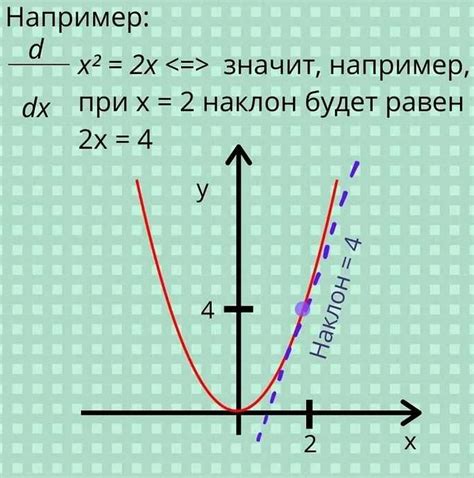
Рассмотрим функцию f(x) = x^2. Для нахождения производной этой функции воспользуемся формулой дифференцирования степенной функции: f'(x) = n * x^(n-1).
Дифференцируя функцию f(x) = x^2, получим f'(x) = 2 * x^(2-1) = 2 * x. Это значит, что производная функции равна удвоенному аргументу.
Например, если подставить x = 3, получим производную функции в точке 3: f'(3) = 2 * 3 = 6. То есть, в данной точке график функции будет иметь наклон 6.
Таким образом, дифференцирование функции позволяет найти ее производную и определить характер ее изменения в различных точках области определения.
Примеры простых функций, которые можно дифференцировать
Продифференцировать функцию означает найти ее производную, то есть вычислить скорость изменения значения функции в каждой точке. Вот несколько примеров простых функций, которые можно легко дифференцировать:
| Функция | Производная |
|---|---|
| f(x) = c | f'(x) = 0 |
| f(x) = x^n | f'(x) = nx^(n-1) |
| f(x) = e^x | f'(x) = e^x |
| f(x) = ln(x) | f'(x) = 1/x |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |
Это лишь некоторые примеры простых функций, которые можно дифференцировать. В общем случае, любую функцию можно продифференцировать, если она является непрерывной и дифференцируемой на заданном интервале.
Основные понятия и определения дифференцирования

Производная функции в некой точке является ее главной характеристикой и выражает скорость изменения функции в данной точке.
Если функция задана аналитически, то ее производная может быть найдена аналитически путем определения производной по правилам дифференцирования.
Дифференцирование позволяет решать различные задачи, связанные с оптимизацией, анализом изменения переменных, а также представляет основу для интегрирования функций.
Процесс дифференцирования основан на концепции пределов и представляет собой нахождение предела отношения приращения функции к приращению аргумента при стремлении последнего к нулю.
Для дифференцирования используются различные правила, такие как правило дифференцирования константы, правило дифференцирования сложной функции и правило дифференцирования степенной функции.
Дифференцирование является неотъемлемой частью математики и находит применение в различных областях, включая физику, экономику и инженерные науки. Оно достаточно сложно и требует понимания основных понятий и определений, описанных выше.
Формулы дифференцирования и их использование
Для дифференцирования функций существуют основные правила, которые позволяют находить производную функции проще и быстрее. Вот некоторые из них:
| Функция f(x) | Производная f'(x) |
| c | 0 |
| x^n | n * x^(n-1) |
| a^x | a^x * ln(a) |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
| e^x | e^x |
| ln(x) | 1/x |
Это лишь небольшой набор формул, которые могут быть использованы для дифференцирования функций. Более сложные функции могут потребовать применения цепного правила или других методов для вычисления производной. Освоив эти формулы, можно упростить процесс дифференцирования и найти точные значения производных различных функций.
Практическое применение дифференцирования
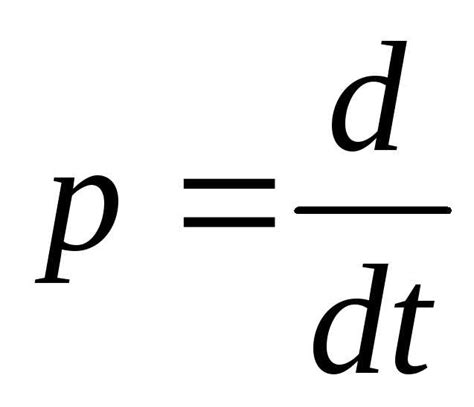
Дифференцирование функций часто используется в различных областях науки и техники для решения различных задач и оптимизации процессов. Вот несколько примеров практического применения дифференцирования:
| Область | Пример применения дифференцирования |
|---|---|
| Физика | Дифференцирование позволяет находить скорость и ускорение объектов в движении, а также решать задачи связанные с теплопроводностью, электричеством и многими другими явлениями. |
| Экономика | Дифференцирование используется для оптимизации процессов производства и распределения ресурсов, анализа рынков, оценки эластичности спроса и многих других экономических задач. |
| Инженерия | Дифференцирование является важным инструментом для анализа и проектирования различных систем, таких как электрические цепи, механические конструкции, алгоритмы управления и многое другое. |
| Медицина | В медицине дифференцирование используется для анализа изменений в организме пациента, выявления патологических процессов, оптимизации лечебных препаратов и дозировок. |
| Информационные технологии | Дифференцирование играет важную роль в обработке и анализе данных, машинном обучении, оптимизации алгоритмов и многих других областях информационных технологий. |
Как видно из приведенных примеров, дифференцирование является неотъемлемым инструментом для решения разнообразных задач и оптимизации процессов в различных областях. Его практическое применение выходит далеко за рамки математических расчетов и играет важную роль в современном мире.
Примеры сложных функций, которые можно дифференцировать
Процесс дифференцирования позволяет найти производную функции в каждой точке ее области определения. И хотя это может показаться сложным и абстрактным, существуют различные примеры сложных функций, для которых можно вычислить производные.
Один из примеров сложных функций, которые могут быть дифференцированы, - это тригонометрические функции. Например, производная функции синуса: если f(x) = sin(x), то f'(x) = cos(x). Аналогично, производная косинуса: если g(x) = cos(x), то g'(x) = -sin(x). А также существуют производные для других тригонометрических функций, таких как тангенс, котангенс, секанс и косеканс.
Другой пример сложной функции, которую также можно дифференцировать, - это логарифмические функции. Например, производная функции натурального логарифма: если h(x) = ln(x), то h'(x) = 1/x. Аналогично, производные для других логарифмических функций, таких как логарифм по основанию a и обратный логарифм.
Следующий пример сложной функции, дифференцируемой в каждой точке своей области определения, - это степенные функции. Например, производная функции x^n, где n - любое вещественное число, равна f'(x) = n * x^(n-1). Это правило также применимо к другим степенным функциям, таким как квадратный корень, кубический корень и т.д.
Кроме того, существуют и другие сложные функции, которые могут быть дифференцированы, такие как экспоненциальные функции (например, производная функции e^x равна f'(x) = e^x) и гиперболические функции (например, производная функции sinh(x) равна f'(x) = cosh(x)).
Важно помнить, что правила дифференцирования различных функций могут существенно отличаться друг от друга, и для точного вычисления производной рекомендуется пользоваться таблицами производных или использовать численные методы.








