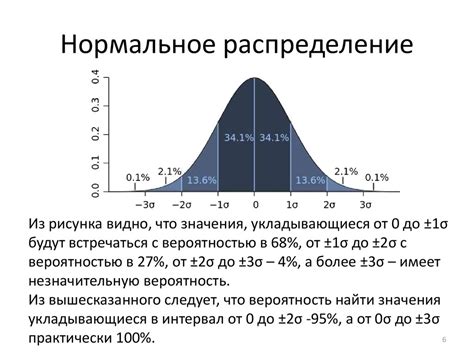
Статистическое правило 3 сигм - это одно из ключевых понятий в теории вероятностей и математической статистике. Оно указывает на то, что большинство наблюдаемых значений в нормальном распределении сосредоточены в пределах трех стандартных отклонений от среднего значения. Это правило стало основой для множества методов анализа данных и нахождения выбросов.
Важно понимать, что нормальное распределение, также известное как гауссово распределение или закон больших чисел, является одним из наиболее распространенных типов вероятностных распределений. Оно описывает множество случайных явлений в природе, экономике, физике и других областях. Нормальное распределение характеризуется симметричной формой и колоколообразной кривой, а среднее значение и стандартное отклонение определяют его положение и разброс.
Правило 3 сигм имеет важный практический смысл, поскольку позволяет нам понять, насколько предсказуемо или необычно какое-либо явление в рамках нормального распределения. Оно утверждает, что около 99,7% наблюдаемых значений лежат в пределах интервала от трех стандартных отклонений ниже и выше среднего значения. То есть, если мы знаем среднее значение и стандартное отклонение, мы можем оценить диапазон, в котором ожидается большинство значений.
Раскрытие правила 3 сигм: значение для нормального распределения
Правило 3 сигм основывается на том, что для нормального распределения около 99,7% наблюдений должны находиться в пределах трех стандартных отклонений от среднего значения. Другими словами, если данные имеют нормальное распределение, то около 99,7% наблюдений должны находиться в диапазоне от μ - 3σ до μ + 3σ, где μ - среднее значение, а σ - стандартное отклонение.
Это правило позволяет определить, какие значения считаются необычными или выбросами в случае, если данные нарушают нормальное распределение. Если наблюдение находится за пределами диапазона от μ - 3σ до μ + 3σ, то оно считается значимым и может указывать на наличие аномалий или ошибок в данных.
Значение правила 3 сигм важно для статистического анализа данных, так как позволяет определить, насколько данные соответствуют нормальному распределению. Если большое количество наблюдений находится вне трех сигм, это может указывать на ненормальность данных, что в свою очередь имеет влияние на результаты статистических тестов и выводы, сделанные на их основе.
Понятие правила 3 сигм
В статистике нормальное распределение (или распределение Гаусса) используется для моделирования случайных величин, таких как результаты измерений, веса, длины и т.д. В нормальном распределении значение среднего и стандартного отклонения играют важную роль.
Правило 3 сигм гласит, что около 68% значений выборки должны находиться в пределах одного стандартного отклонения от среднего значения, примерно 95% значений - в пределах двух стандартных отклонений, и около 99.7% значений - в пределах трех стандартных отклонений.
Таким образом, для нормального распределения правило 3 сигм позволяет определить, какие значения можно считать стандартными, а какие - редкими или выбросами.
Применение правила 3 сигм в статистике
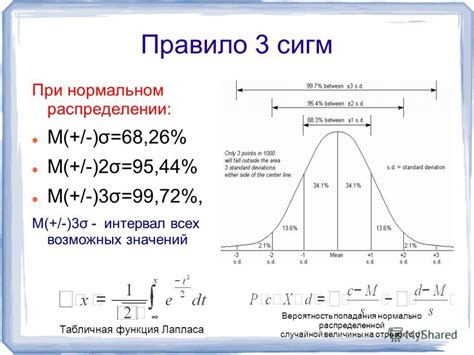
Правило 3 сигм широко используется в статистике для определения вероятностного интервала вокруг среднего значения нормального распределения. Согласно этому правилу, около 99,7% значений случайной величины должно лежать в пределах трех стандартных отклонений от среднего.
Используя правило 3 сигм, можно оценить разброс данных вокруг среднего значения и определить, насколько наблюдаемые значения отклоняются от ожидаемых. Если значение отклоняется на более чем три стандартных отклонения от среднего, то это может указывать на наличие выбросов или необычных значений в данных.
Правило 3 сигм также может быть использовано для определения вероятности наблюдаемого значения случайной величины. Если значение отклоняется на одно стандартное отклонение от среднего, то оно имеет вероятность около 68%, на два стандартных отклонения - около 95%, и на три стандартных отклонения - около 99,7%.
Однако следует помнить, что все эти оценки и интерпретации основаны на предположении о нормальном распределении данных и могут быть неприменимы для других типов распределений. Поэтому перед применением правила 3 сигм необходимо провести анализ и убедиться в соблюдении предпосылок.
Основные характеристики нормального распределения
- Симметрия: Нормальное распределение симметрично относительно своего среднего значения, которое также является медианой распределения. Это означает, что вероятности для значений, расположенных справа и слева от среднего, равны.
- Значение среднего и медианы: Среднее значение (математическое ожидание) и медиана нормального распределения совпадают и находятся в центре распределения.
- Точные значения крайних квантилей: У нормального распределения точно известны значения крайних квантилей. Например, значение 95-го процентиля нормального распределения составляет приблизительно 1.96 стандартных отклонения.
- Концентрация значений: Нормальное распределение сравнительно более "концентрировано" вокруг своего среднего значения по сравнению с другими распределениями. Иными словами, значения выборки, находящиеся далеко от среднего значения, менее вероятны.
- Параметры среднего и стандартного отклонения: Нормальное распределение полностью определяется двумя параметрами: средним значением (μ) и стандартным отклонением (σ). Среднее значение определяет центр распределения, а стандартное отклонение - его размах.
Доказательство применимости правила 3 сигм к нормальному распределению
Нормальное распределение, также известное как распределение Гаусса или закон больших чисел, является одним из самых распространенных распределений в статистике. Оно характеризуется симметричной формой графика и показывает, как вероятность значения наблюдаемой случайной величины уменьшается по мере удаления от среднего значения.
Доказательство применимости правила 3 сигм к нормальному распределению основывается на следующих фактах:
- Примерно 68% значений наблюдаемой случайной величины лежат в пределах одного стандартного отклонения от среднего значения.
- Примерно 95% значений наблюдаемой случайной величины лежат в пределах двух стандартных отклонений от среднего значения.
- Примерно 99.7% значений наблюдаемой случайной величины лежат в пределах трех стандартных отклонений от среднего значения.
Эти факты можно объяснить с помощью свойств нормального распределения. Для распределения, где среднее значение равно 0 и стандартное отклонение равно 1, значения, лежащие в пределах одного стандартного отклонения от среднего значения, составляют примерно 68% от общего числа значений. Точно так же, значения, лежащие в пределах двух и трех стандартных отклонений, составляют примерно 95% и 99.7% соответственно.
Используя правило 3 сигм, мы можем оценить разброс данных и определить, насколько значения отклоняются от среднего в нормальном распределении. Это может быть полезно для анализа данных, прогнозирования результатов и принятия решений в различных сферах, таких как физика, экономика, медицина и т.д.
Определение стандартного отклонения в нормальном распределении
Стандартное отклонение обозначается символом σ (сигма) и вычисляется как квадратный корень из дисперсии. Дисперсия в свою очередь измеряет средний квадрат отклонения значений от их среднего значения.
В нормальном распределении, также известном как гауссово распределение, стандартное отклонение имеет важное значение. Оно определяет форму и ширину распределения, а также позволяет анализировать вероятность того, что случайно выбранное значение будет отклоняться от среднего значения на определенное количество стандартных отклонений.
Расчет значений 3 сигм для нормального распределения
Стандартное отклонение (сигма) является мерой разброса значений относительно среднего значения в нормальном распределении. Правило 3 сигм гласит, что в нормальном распределении около 99.7% наблюдений попадают в диапазон, ограниченный тремя стандартными отклонениями от среднего значения.
Для расчета значений 3 сигм в нормальном распределении необходимо выполнить следующие шаги:
| Шаг | Формула | Результат |
|---|---|---|
| 1 | Среднее значение | μ |
| 2 | Стандартное отклонение | σ |
| 3 | Значение начала диапазона (3 сигмы ниже среднего значения) | μ - 3σ |
| 4 | Значение конца диапазона (3 сигмы выше среднего значения) | μ + 3σ |
Принимая во внимание это правило, мы можем оценить вероятность того, что случайное наблюдение из нормального распределения попадет в определенный диапазон значений. Таким образом, расчет значений 3 сигм для нормального распределения является важным инструментом для анализа статистических данных и определения аномалий.
Вероятность нахождения значений за пределами 3 сигм
Правило 3 сигм в статистике указывает, что для нормально распределенной случайной величины 99.7% ее значений находятся в пределах трех стандартных отклонений от среднего значения. Иными словами, только 0.3% значений могут быть за пределами этого диапазона.
Вероятность нахождения значений за пределами 3 сигм может быть вычислена с использованием таблицы нормального распределения или формулы стандартного нормального распределения. Например, для нормального распределения со средним значением μ и стандартным отклонением σ, вероятность нахождения значения вне диапазона трех стандартных отклонений от μ может быть найдена как:
P(|X - μ| > 3σ) = P(X > μ + 3σ) + P(X
Здесь P(X > μ + 3σ) представляет вероятность нахождения значения выше верхней границы диапазона, а P(X
Общая вероятность нахождения значений за пределами 3 сигм равна сумме этих двух вероятностей и составляет всего 0.3%.
Это свойство нормального распределения широко используется для оценки и анализа данных, так как позволяет определить, насколько вероятно найденное значение является аномальным или представляет собой случайность.
| Вероятность | Нахождение значений за пределами 3 сигм |
|---|---|
| P(|X - μ| > 3σ) | 0.3% |








