Период функции является одним из важных понятий в математике, особенно в области анализа. Он представляет собой расстояние между двумя ближайшими значениями функции, при которых она принимает одинаковое значение. В данной статье мы рассмотрим случай, когда период функции равен 2.
Для начала, рассмотрим формулу для функции с периодом 2: f(x + 2) = f(x). Это значит, что если мы добавим к аргументу функции 2, то получим такое же значение функции, как если бы мы использовали исходное значение аргумента. В других словах, функция повторяется через каждые 2 единицы аргумента.
Закономерности, связанные с периодичностью функции, могут быть истолкованы на многих уровнях. Например, функция с периодом 2 может соответствовать ситуациям, повторяющимся каждые 2 временных единицы или пространственных интервала. Это может быть полезным при моделировании и анализе таких процессов, как движение, колебания и циклические явления.
Для лучшего понимания концепции периода функции равного 2, рассмотрим пример конкретной функции. Пусть у нас есть функция синуса, f(x) = sin(x). Оказывается, функция синуса является периодической и ее период равен 2π. Это означает, что функция повторяется снова и снова через каждые 2π единицы аргумента. То есть для всех целых чисел n, выполняется равенство sin(x + 2πn) = sin(x), где n - целое число. Этот пример показывает, что период функции может быть использован для описания повторяющихся узоров и циклов в функциях.
Что такое период функции?
Математически, функция f(x) имеет период, если выполняется следующее условие:
f(x + T) = f(x)
где T - период функции.
Период функции может быть константой или вычисляемым значением в зависимости от типа функции. Некоторые простые примеры функций с известными периодами включают синусоиду (период 2П), косинусоиду (период 2П) и тангенс (период П).
Понимание периода функции может быть полезно при решении уравнений, определении амплитуды и фазы функции, а также оценке поведения функции на длительных временных интервалах.
Определение и объяснение понятия
Другими словами, период функции - это расстояние между двумя последовательными повторениями функции. Это время, через которое функция возвращается к своему начальному значению или повторяет свой график.
Чтобы найти период функции, мы должны найти длину интервала, при которой функция повторяется. Для периодических функций, таких как синусоида или косинусоида, период очевиден и можно определить с помощью формул или графиков.
Но в некоторых случаях найти период функции может быть сложно или неочевидно. Например, для функций, заданных различными формулами на различных интервалах, найти период может потребовать дополнительного анализа, использования математических методов и алгоритмов, таких как методы численного анализа.
Формула вычисления периода функции

f(x) = f(x + T)
Другими словами, функция повторяет свое значение с периодичностью T.
Формула для вычисления периода функции может зависеть от ее типа и заданной функции:
- Для функции синуса и косинуса, период равен 2π.
- Для линейной функции f(x) = kx + b период равен 0, так как функция не повторяется с какой-либо периодичностью.
- Для квадратичной функции f(x) = ax^2 + bx + c, где a ≠ 0, период может быть найден с помощью вычисления дискриминанта и формулы, зависящей от значения дискриминанта:
- Если дискриминант D = b^2 - 4ac > 0, то функция имеет два корня и период равен разности этих корней.
- Если дискриминант D = b^2 - 4ac = 0, то функция имеет один корень и период равен нулю.
- Если дискриминант D = b^2 - 4ac , то функция не имеет корней и период также равен нулю.
Важность понимания периода функции
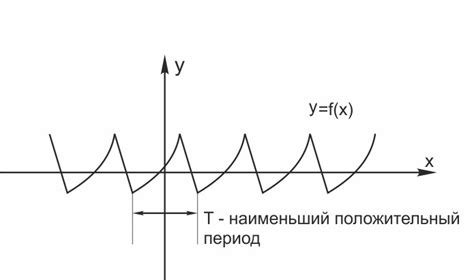
Период функции определяет, через сколько единиц времени функция повторяет свое значение. Другими словами, это наименьшее положительное число, при котором функция принимает одинаковые значения. Например, если период функции равен 2, то ее значение повторяется через каждые 2 единицы времени.
Знание периода функции позволяет нам делать предсказания о поведении функции на протяжении определенного времени. С помощью периода мы можем определить, когда функция достигнет максимума или минимума, а также выявить ее симметричность относительно оси или графика.
Понимание периода функции также помогает нам решать уравнения и делать графические представления функций. Например, зная период функции, мы можем построить график, повторяющийся через определенные интервалы времени, что упрощает визуализацию сути функции.
Знание периода функции также полезно для решения практических задач. Например, если мы изучаем зависимость затрат компании от времени, то знание периода может помочь нам предсказывать, когда будут происходить периодические изменения затрат и планировать свою деятельность соответствующим образом.
В итоге, понимание периода функции помогает нам более глубоко анализировать ее характеристики и свойства, делать предсказания о ее поведении, решать уравнения и визуализировать функцию. Поэтому осознание и умение использовать понятие периода является важным инструментом в математике и других областях, где функции играют важную роль.
Примеры функций с периодом 2
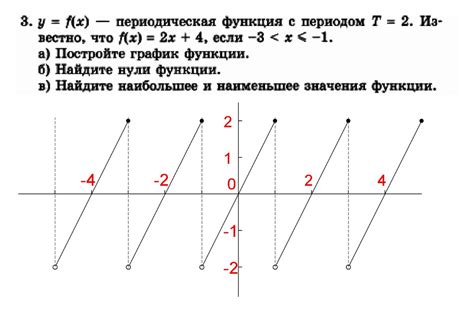
Период функции определяет, через какой интервал аргумента функция повторяется. Для функций с периодом 2 это значит, что значение функции повторяется через каждые 2 единицы аргумента.
Рассмотрим несколько примеров функций с периодом 2:
- Функция синуса: y = sin(x)
- Функция косинуса: y = cos(x)
- Функция тангенса: y = tan(x)
- Функция секанса: y = sec(x)
- Функция котангенса: y = cot(x)
Функция синуса имеет период 2π. Это означает, что значение синуса повторяется через каждые 2 радиана аргумента. Например, значение синуса при x=0 равно 0, при x=2π также будет равно 0.
Функция косинуса также имеет период 2π. Значения косинуса повторяются через каждые 2 радиана аргумента. Например, значение косинуса при x=0 равно 1, при x=2π также будет равно 1.
Функция тангенса имеет период π. То есть значения тангенса повторяются через каждое π единиц аргумента. Например, значение тангенса при x=0 равно 0, при x=π также будет равно 0.
Функция секанса также имеет период 2π. Значения секанса повторяются через каждые 2 радиана аргумента. Например, значение секанса при x=0 равно 1, при x=2π также будет равно 1.
Функция котангенса также имеет период π. Значения котангенса повторяются через каждое π единиц аргумента. Например, значение котангенса при x=0 равно ∞, при x=π также будет равно ∞.
И это лишь некоторые из множества функций, которые имеют период 2. Знание периода функции позволяет нам более глубоко изучать их свойства и поведение на графике.
Графическое представление функции с периодом 2
Период функции может быть определен как наименьшая положительная величина T, при которой функция повторяет свое значение. Например, функция с периодом 2 будет иметь значение в точке x равное значению в точке x + 2.
График функции с периодом 2 будет повторяться через каждые 2 единицы по оси x. Изображение графика этой функции будет идентично на каждом интервале длиной 2.
Например, рассмотрим функцию f(x) = sin(x). В данном случае, период функции T = 2π, то есть график функции sin(x) повторяется через каждые 2π радиан.
Графическое представление функции sin(x) с периодом 2 можно получить, нарисовав несколько периодов этой функции на координатной плоскости. На оси x отмечаем точки 0, 2, 4 и т.д., а на оси y отмечаем значения функции sin(x) в этих точках. Затем соединяем полученные точки прямыми линиями, и получаем график функции sin(x) с периодом 2, который представляет собой повторяющуюся волнообразную кривую.
Применение периода функции в реальной жизни
Период функции играет важную роль в различных областях жизни и науки. Он позволяет анализировать и предсказывать повторяющиеся процессы и явления, а также определять частоту и регулярность их изменений.
Например, в физике период функции может быть использован для изучения колебаний и волн. На практике это может быть полезно при проектировании маяков, радиосистем, лазеров и других устройств, которые основаны на периодических процессах.
В математике период функции часто используется для анализа графиков и числовых рядов. Знание периода позволяет определить поведение функции на протяжении определенного интервала и найти решение уравнений или систем уравнений.
В экономике период функции может быть применен для анализа рыночных циклов, таких как колебания спроса и предложения, изменения цен и процентных ставок. Это помогает экономистам делать прогнозы, планировать бюджеты и разрабатывать эффективные стратегии управления.
Период функции также имеет применение в музыке, где он определяет частоту звуковых волн и их гармоничность. Это позволяет создавать мелодии, гармонии и ритмы, которые приятно воспринимаются слушателем.
Таким образом, понимание и применение периода функции в реальной жизни являются важными для различных областей деятельности и позволяют получать ценную информацию о поведении и изменениях различных процессов и явлений.








