В математике дроби являются одним из важных понятий, которые позволяют нам работать с рациональными числами. Но что означают натуральные значения дробей и как понять их смысл? Давайте разберемся.
Натуральные значения дробей представляют собой числа, которые можно представить в виде отношения двух целых чисел. Например, дроби 1/2, 3/4, 2/5 и т.д. Числитель дроби указывает на количество частей, которые мы берем из целого числа, а знаменатель показывает, на сколько частей мы делим целое число. Таким образом, дробь 1/2 означает, что мы берем одну часть из двух возможных.
Для понимания смысла натуральных значений дробей важно уметь интерпретировать их в реальных ситуациях. Например, если у нас есть пицца, разрезанная на две части, и мы берем одну из этих частей, то мы можем представить это в виде дроби 1/2. Если мы берем три четверти пирога из четырех возможных, то это будет дробь 3/4. Таким образом, натуральные значения дробей помогают нам описывать доли и части целого числа.
Натуральные значения дробей имеют важное практическое применение в различных областях науки и жизни. Например, они используются в финансовой сфере для рассчета процентных ставок, в рецептах для указания количества ингредиентов, в геометрии для измерения углов и длин отрезков и т.д. Поэтому понимание натуральных значений дробей является важным навыком для решения различных задач и заданий в математике и других научных дисциплинах.
Таким образом, понимание натуральных значений дробей и их смысла позволяет нам лучше обращаться с рациональными числами и использовать их в реальных ситуациях. Умение интерпретировать дроби поможет нам решать задачи различной сложности в нашей повседневной жизни и в профессиональной деятельности.
Понимание натуральных значений дробей: основные концепции и принципы

Основные концепции, которые необходимо понять при работе с натуральными значениями дробей, включают:
| Концепция | Описание |
|---|---|
| Числитель и знаменатель | Числитель дроби указывает на количество долей, а знаменатель определяет количество долей, на которые целое делится. |
| Сравнение дробей | Дроби можно сравнивать между собой с помощью операций сравнения, таких как больше, меньше или равно. |
| Приведение к общему знаменателю | Для выполнения операций сложения и вычитания дробей, необходимо привести их к общему знаменателю. |
Принципы работы с натуральными значениями дробей заключаются в следующем:
- Числитель и знаменатель являются основными компонентами дроби.
- Знаменатель не может быть равен нулю, так как деление на ноль не определено.
- Дроби можно сокращать, то есть упрощать, путем выделения общих множителей числителя и знаменателя.
- Приведение дробей к общему знаменателю позволяет выполнить операции сложения и вычитания.
- При умножении дробей перемножаются числители и знаменатели, а при делении умножаются числитель одной дроби на знаменатель другой.
Понимание и применение этих концепций и принципов позволяет работать с натуральными значениями дробей, выполнять математические операции и решать задачи, связанные с долей от целого. Это важные навыки, которые применяются в различных областях, таких как финансы, инженерия, медицина и другие.
Что такое дробь и как ее понять
Для понимания значения дробей необходимо осознать, что они представляют доли целого числа или единицы. Например, дробь 1/2 означает одну половину, 3/4 - три четверти, а 2/3 - две трети целого числа или единицы.
Дроби могут иметь как натуральные, так и десятичные значения. Например, дробь 1/2 в десятичной форме будет равна 0.5. Это означает, что одна половина равна половине десятичного числа, которое равно 0.1, умноженному на 5.
Понимание значения дробей особенно важно для решения задач, связанных с долями, долями величин и процентами. Например, при расчете скидки, увеличении или уменьшении чего-либо на определенную долю, необходимо знать, как интерпретировать значение дроби и применить его в практике.
Итак, дробь - это способ представления долей числа или единицы. Знание и понимание значений дробей помогает в анализе и решении задач, связанных с долями и процентами, и является важным навыком в математике и повседневной жизни.
Типы натуральных значений дробей и их смысл
Натуральные значения дробей можно разделить на несколько типов в зависимости от своего смысла и представления. В основе каждого типа лежит отношение между двумя натуральными числами, которое задает дробь.
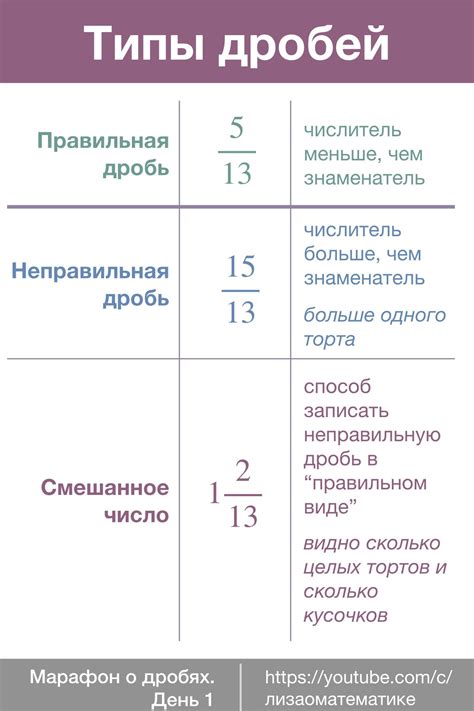
1. Простые дроби: Простые дроби представляют отношение между числителем и знаменателем. Числитель указывает на количество одинаковых частей, а знаменатель указывает на общее количество частей, из которых состоит целое. Например, дробь 1/2 означает, что имеется одна половина целого.
2. Сложные дроби: Сложные дроби представляют отношение между одной или несколькими целыми числами и дробью. Они имеют вид «целое число + дробь». Например, дробь 2 3/4 означает, что имеется две целых части и три четверти целой части.
3. Десятичные дроби: Десятичные дроби представляют отношение между числителем и знаменателем в десятичной системе счисления. Они имеют вид «целое число, десятичная запятая, десятичные цифры». Например, дробь 0.75 означает, что имеется 75 сотых части целого числа.
4. Проценты: Проценты представляют отношение между числителем и знаменателем в процентной форме, где числитель указывает на число процентов, а знаменатель указывает на 100. Например, дробь 50% означает, что имеется 50 частей из 100, что равно половине целого.
5. Разделительные дроби: Разделительные дроби представляют отношение между числителем и знаменателем в форме дроби с целой и десятичной частью, разделенными запятой или точкой. Это используется, например, для обозначения даты или времени. Например, дробь 31.12 означает, что имеется 31 день и 12 месяцев, что соответствует последнему дню года.
Важно понимать смысл и значение каждого типа натуральных значений дробей, чтобы правильно интерпретировать и использовать их в различных математических и практических задачах.
| Тип дроби | Пример | Смысл |
|---|---|---|
| Простая дробь | 1/2 | Одна половина целого |
| Сложная дробь | 2 3/4 | Две целых части и три четверти целой части |
| Десятичная дробь | 0.75 | Семьдесят пять сотых части целого числа |
| Процент | 50% | Пятьдесят частей из ста, половина целого |
| Разделительная дробь | 31.12 | Тридцать один день и двенадцать месяцев, последний день года |
Примеры натуральных значений дробей в повседневной жизни
- Разделение пиццы: Если у вас есть целая пицца и несколько голодных друзей, то единицей в этом случае может быть часть пиццы, которую получает каждый друг. Например, если вы поделите пиццу на 8 частей и каждый друг съест по 3/8 пиццы, то каждый получит натуральное значение дроби.
- Дележ счета в ресторане: При совместном посещении ресторана с друзьями часто приходится делить счет. Если общая сумма составляет, например, 1000 рублей, и вы решите заплатить 2/5 от счета, то это будет еще один пример натурального значения дроби.
- Измерение времени: Измерение времени также может быть выражено в дробных значениях. Например, если вы провели 2 часа и 30 минут на занятиях, то это может быть записано как 2 1/2 часа.
- Расход топлива: Дробные значения также могут использоваться для измерения расхода топлива. Например, если ваш автомобиль проезжает 1/4 галлона бензина на милю, то это будет означать, что для преодоления каждой мили вам потребуется 1/4 галлона топлива.
Это всего лишь несколько примеров, как дробные значения используются в повседневной жизни. Знание и понимание натуральных значений дробей позволяет нам более точно и полно измерять и описывать реальный мир.
Как правильно интерпретировать натуральные значения дробей

Натуральные значения дробей представляют собой части от целого числа и имеют конкретный смысл, который может быть интерпретирован в различных контекстах. Важно понять, что дроби могут описывать доли от целого, соотношения между величинами или другие аспекты реального мира.
Дроби, где числитель больше знаменателя, можно интерпретировать как числа больше единицы. Например, дробь 3/2 означает, что у нас есть 3 элемента размером с половину стандартного элемента. В контексте рецептов это может означать, что нам нужно взять полтора раза больше рецептурных ингредиентов.
Дроби, где числитель равен знаменателю, равны единице. Например, дробь 4/4 означает, что мы берем целую единицу или все, что имеется. В математических задачах это может олицетворять собой полную величину или объем.
Дроби, где числитель меньше знаменателя, могут описывать доли от целого, как вариант геометрического измерения. Например, дробь 1/2 означает, что мы берем половину от значения, размера или объема.
При рассмотрении дробей с отрицательным числителем или знаменателем следует помнить, что они представляют отрицательную величину или соотношение. Например, дробь -2/3 может означать, что у нас есть отрицательное отношение между двумя элементами, где один элемент больше другого в три раза.
Интерпретация натуральных значений дробей зависит от контекста, в котором они используются, и может варьироваться в различных областях знаний. Важно учитывать этот контекст и уметь применять соответствующие значения дробей для решения задач и описания действительных ситуаций.








