Что значит найти решение нелинейного уравнения?

Нелинейные уравнения являются важным инструментом в математике и науке, поскольку могут описывать сложные зависимости и явления, которые не могут быть описаны линейными уравнениями. Однако, нахождение точного аналитического решения нелинейного уравнения часто оказывается сложной задачей.

В этой статье мы рассмотрим различные методы, позволяющие найти решение нелинейного уравнения. Мы начнем с простых и широко применяемых методов, таких как метод подстановки и метод графического приближения. Затем мы перейдем к более сложным методам, таким как метод Ньютона и метод простой итерации.

Основной идеей всех этих методов является нахождение такого значения переменной, при котором уравнение принимает равенство. Для достижения этой цели применяются различные алгоритмы и итерационные процессы. Некоторые методы требуют начального приближения, другие могут быть применены для решения нелинейных систем уравнений.

Алгоритм поиска решения

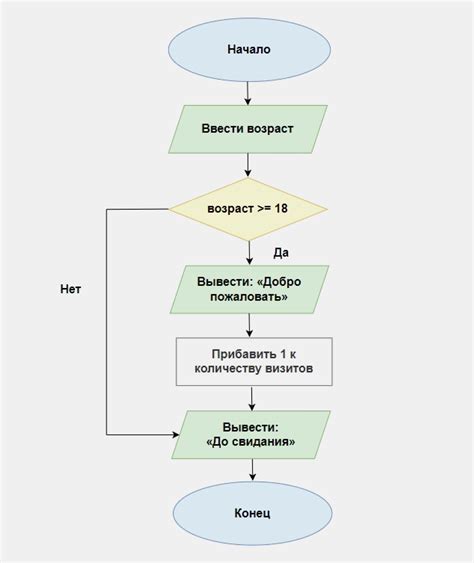
Алгоритм поиска решения методом ньютона:

1. Выбрать начальное приближение x₀.
2. Вычислить значение функции f(x) и ее производной f'(x) в точке x₀.
3. Вычислить корень уравнения x₁ = x₀ - f(x₀) / f'(x₀).
4. Проверить точность решения. Если разница между x₀ и x₁ достаточно мала, то x₁ является приближенным значением решения. Если точность не достигнута, то присвоить x₀ значение x₁ и вернуться к шагу 2.

Метод ньютона может быть применен для решения таких уравнений, в которых производная функции известна и непрерывна в заданном интервале. Однако, необходимо быть осторожным при выборе начального приближения, так как неправильный выбор может привести к расходимости или сходимости к ложному корню.

Важно отметить, что метод ньютона не всегда гарантирует нахождение решения, так как итерационный процесс может остановиться на локальном минимуме или максимуме функции. Поэтому требуется проводить дополнительные проверки, например, наличие одной или нескольких параллельных прямых.

В заключение можно сказать, что алгоритм поиска решения нелинейного уравнения является сложной задачей, требующей тщательного анализа и выбора подходящего метода в зависимости от характеристик уравнения.

Метод Ньютона-Рафсона для нелинейных уравнений

Для применения метода Ньютона-Рафсона необходимо иметь начальное приближение корня уравнения. Затем на каждой итерации метода используется формула:

x_n+1 = x_n - f(x_n) / f'(x_n)

где x_n+1 - новое приближение корня, x_n - предыдущее приближение корня, f(x_n) - значение функции в точке x_n, f'(x_n) - значение производной функции в точке x_n.

Итерации продолжаются до тех пор, пока не будет достигнута заданная точность или не будет найдено достаточно близкое приближение корня уравнения.

Основным преимуществом метода Ньютона-Рафсона является его быстрая сходимость, особенно вблизи корня. Однако этот метод может не работать, если начальное приближение выбрано неправильно или если производная функции близка к нулю вблизи корня.

Метод Ньютона-Рафсона широко применяется в различных областях, таких как физика, экономика и инженерия, для решения нелинейных уравнений. Он позволяет быстро и эффективно находить корни уравнений и является важным инструментом аналитического и численного анализа.

Приближенные методы поиска решений

При решении нелинейных уравнений, когда аналитическое решение неизвестно или нереально найти, можно использовать приближенные методы. Эти методы позволяют найти приближенное значение корня уравнения с заданной точностью.

Один из самых популярных приближенных методов - метод половинного деления. Он основан на принципе инкрементного поиска корня. Данный метод заключается в последовательном делении отрезка, на котором существует корень, наполовину и выборке отрезка, на котором достигается корень. Процесс повторяется до тех пор, пока не будет достигнута желаемая точность решения. Метод половинного деления прост в реализации, но требует большого числа итераций для достижения точного результата.

Другим приближенным методом является метод Ньютона. Он основан на приближенном вычислении производной функции, затем итеративно находит корень уравнения. Метод Ньютона обладает быстрой сходимостью, но требует знания аналитического выражения производной функции. Для функций, где аналитическое выражение производной сложно или невозможно получить, метод Ньютона не применим.

Также существуют и другие приближенные методы, такие как метод секущих, метод простой итерации и метод Брента. Каждый из этих методов имеет свои преимущества и недостатки в зависимости от особенностей функции и требуемой точности решения.

При выборе приближенного метода необходимо учесть тип уравнения, его свойства и требуемую точность результата. Приближенные методы позволяют получить решение нелинейных уравнений в тех случаях, когда аналитическое решение невозможно или слишком сложно получить.

Полное раскрытие алгоритма

Для нахождения решения нелинейного уравнения мы будем использовать алгоритм метода Ньютона. Этот алгоритм позволяет находить приближенные значения корней уравнения и уточнять их с каждой итерацией.

1. Выбираем начальное приближение для корня уравнения.
2. Подставляем это приближение в уравнение и вычисляем значение.
3. Вычисляем производную функции и подставляем значение приближения в неё.
4. Вычисляем новое приближение для корня уравнения по формуле: x_новое = x_старое - f(x_старое)/f'(x_старое)
5. Повторяем шаги 2-4 до сходимости алгоритма.

Метод Ньютона обладает высокой скоростью сходимости, однако требует наличия аналитического выражения для производной функции. Если такое выражение неизвестно, можно воспользоваться численными методами для приближённого вычисления производной.

После окончания итераций алгоритма, полученное приближенное значение корня можно проверить, подставив его в уравнение и оценив его точность. Если решение удовлетворяет условиям задачи, то оно является допустимым решением нелинейного уравнения.

Итерационные методы решения нелинейных уравнений

Метод простой итерации основан на принципе последовательных приближений. Он заключается в том, что искомый корень уравнения представляется в виде точки пересечения графика функции f(x) и прямой y=x. Далее, используя рекуррентную формулу, мы последовательно находим новые значения корня, до тех пор пока не достигнем требуемой точности.

Для применения метода простой итерации необходимо выполнение ряда условий, включая сходимость функции f(x) на заданном интервале, производную функции, удовлетворяющую выделенному условию сходимости, а также начальное приближение корня, близкое к искомому значению.

Еще одним эффективным итерационным методом является метод Ньютона. Он основан на использовании производной функции, итерационной формулы основанной на применении разложения в ряд Тейлора, и последовательного приближения к корню.

Метод Ньютона позволяет достичь высокой скорости сходимости, однако требует более высокой вычислительной мощности, чем метод простой итерации. Он также может иметь проблемы с сходимостью для некоторых функций, особенно если начальное приближение корня выбрано неудачно.

Важным аспектом итерационных методов является контроль сходимости, то есть определение критерия остановки итерационного процесса. Обычно критерием остановки является достижение требуемой точности, или установление максимального числа итераций.

Таким образом, итерационные методы представляют собой эффективный инструмент для решения нелинейных уравнений. Они обладают своими особенностями и требованиями, и выбор конкретного метода зависит от конкретной задачи и условий ее решения.

Примеры применения алгоритма в реальной жизни

Алгоритм решения нелинейных уравнений находит широкое применение в реальной жизни, в различных областях науки и техники. Вот несколько примеров:

1. Физика: Одним из основных примеров является использование алгоритма для решения уравнений, описывающих движение тел в пространстве. Например, при моделировании движения планет в солнечной системе или при расчете траектории полета ракеты. Вычисление нужных значений нелинейных уравнений позволяет прогнозировать поведение объектов и оценивать их характеристики.

2. Финансы: Алгоритмы решения нелинейных уравнений широко применяются в финансовой сфере, в частности при моделировании поведения финансовых инструментов. Например, для определения оптимальных цен на акции, расчета параметров портфеля или определения доходности инвестиций. Решение нелинейных уравнений позволяет анализировать сложные финансовые процессы и прогнозировать возможные сценарии.

3. Инженерия: В инженерной сфере алгоритмы решения нелинейных уравнений используются для оптимизации процессов и поиска наилучших решений. Например, при проектировании электрических схем, оптимизации конструкций или при настройке параметров устройств. Алгоритмы позволяют учесть различные факторы и достичь максимальных результатов при проектировании и эксплуатации различных систем.

4. Медицина: В медицине алгоритмы решения нелинейных уравнений применяются, например, для моделирования фармакокинетики лекарственных препаратов. Они позволяют определить оптимальные дозировки и расчеты для достижения требуемого эффекта и снижения рисков. Также алгоритмы могут использоваться для анализа биологических данных и построения моделей жизненно важных функций организма.

Это только небольшая часть областей, где алгоритмы решения нелинейных уравнений находят свое применение. Множество задач в различных сферах требуют точных решений нелинейных уравнений для определения параметров, прогнозирования результатов и оптимизации процессов.