Поиск корня уравнения, который принадлежит заданному отрезку, является важной задачей в математике. Такая задача возникает в различных областях, включая физику, экономику, компьютерные науки и другие. Наличие алгоритмов и методов для решения этой задачи позволяет нам находить значения неизвестных, оптимизировать процессы, прогнозировать результаты и многое другое.
Существует несколько методов для нахождения корня уравнения на заданном отрезке. Один из них - метод половинного деления. Суть этого метода заключается в поиске значения функции в середине отрезка, затем выборе половины отрезка, на котором функция имеет разные знаки. Таким образом, на каждой итерации мы сокращаем отрезок, содержащий корень. Процесс продолжается до тех пор, пока не будет достигнута необходимая точность.
Пример: рассмотрим уравнение f(x) = x^2 - 4. Найдем его корень на отрезке [1, 3].
Сначала найдем значения функции в начальных точках отрезка: f(1) = -3 и f(3) = 5. Изменившись нашей стратегией, выберем новый отрезок, в котором функция имеет разные знаки: [1, 2]. Затем найдем значение функции в середине нового отрезка: f(2) = 0. Таким образом, мы получили корень уравнения - число 2, которое принадлежит отрезку [1, 3].
Это лишь один из методов для нахождения корня уравнения, принадлежащего отрезку. В зависимости от конкретной задачи и условий возможно применение других методов, таких как метод хорд, метод Ньютона и многие другие. Знание этих методов позволяет эффективно решать задачи и находить неизвестные значения.
Определение задачи

Для решения такой задачи существуют различные методы, которые позволяют приближенно найти корень уравнения на заданном отрезке с заданной точностью.
Основная идея методов состоит в построении последовательности приближенных значений корня, итеративной оценке его местоположения и постепенном приближении к нужному значению.
Методы нахождения корня уравнения на отрезке могут применяться в различных областях, таких как математика, физика, экономика и др. Они являются важным инструментом для решения многих задач, связанных с поиском оптимальных значений, моделированием систем и т.д.
| Примеры задач: | Методы нахождения корня: |
|---|---|
| Решение уравнения f(x) = 0 | Метод бисекции (деления отрезка пополам), метод Ньютона (касательных) |
| Нахождение максимума или минимума функции | Метод золотого сечения, метод парабол, метод Фибоначчи |
| Оценка параметров в моделях | Метод наименьших квадратов, метод максимального правдоподобия |
Выбор конкретного метода зависит от характера задачи, доступных ресурсов и требуемой точности. При решении задачи необходимо учитывать ограничения на отрезок, а также возможность наличия нескольких корней.
Необходимость нахождения корня на отрезке
Нахождение корня на отрезке актуально в следующих случаях:
1. Уточнение решения уравнения. Если известно, что корень находится в определенном интервале, нахождение решения в этом интервале может помочь уточнить его значение и дать более точный результат. Например, при решении физической задачи, когда корень соответствует физической величине, ограничение поиска корня на конкретный отрезок может быть важным ограничением.
2. Ограничение области решения. Иногда уравнение имеет несколько корней, но для конкретных целей требуется найти только корни, находящиеся на заданном отрезке. Например, в задаче нахождения времени пересечения двух объектов на плоскости, интересуют только корни, удовлетворяющие условию временного интервала.
Для нахождения корня на отрезке можно использовать различные методы, включая метод половинного деления, метод секущих, метод хорд и др. Конкретный метод выбирается в зависимости от характеристик уравнения и требуемой точности результата.
Заметка: при выборе метода исследование свойств уравнения и его графика может помочь сократить время вычислений и повысить точность результата.
Методы нахождения корня

Нахождение корня уравнения на заданном отрезке требует применения специальных методов. В данном разделе мы рассмотрим два основных метода: метод половинного деления и метод Ньютона.
Метод половинного деления основан на принципе деления отрезка пополам. Сначала выбирается начальный отрезок, затем производится итерационный процесс, в ходе которого отрезок делится пополам и определяется, в какой половине содержится корень. Процесс повторяется до тех пор, пока не будет достигнута необходимая точность.
Метод Ньютона основан на идеи линеаризации функции вблизи точки приближения. Сначала выбирается начальное приближение, затем производится итерационный процесс, в ходе которого вычисляется новое приближение с использованием значения функции и ее производной в предыдущей точке. Процесс повторяется до достижения необходимой точности.
| Метод | Описание |
|---|---|
| Метод половинного деления | Позволяет находить корень путем деления отрезка пополам |
| Метод Ньютона | Позволяет находить корень путем линеаризации функции и использования значения функции и ее производной |
Метод половинного деления
Алгоритм метода половинного деления следующий:
- Выбираются начальные границы отрезка, на котором будет искаться корень уравнения.
- На каждой итерации вычисляется середина отрезка и значение функции в этой точке.
- Если значение функции в середине отрезка равно нулю, то корень найден и алгоритм завершается.
- Иначе, происходит проверка знаков функции на концах и середине отрезка:
- Если знаки на концах и середине отрезка совпадают, то корень находится на другом половине отрезка и отбрасывается та половина, в которой значения функции имеют такой же знак.
- Если знаки разные, то корень находится на отброшенной половине отрезка.
Метод половинного деления имеет хорошую сходимость и гарантирует нахождение корня с заданной точностью. Однако он требует достаточно большого числа итераций для нахождения корня, если значение функции слишком близко к нулю.
Пример использования метода половинного деления:
function halfDivisionMethod(a, b, f, epsilon) {
let x;
let iteration = 0;
do {
x = (a + b) / 2;
if (f(a) * f(x) epsilon);
return { x, iteration };
}
// Пример использования функции
const f = x => x * x - 4; // уравнение f(x) = x^2 - 4 = 0
const a = -2; // левая граница отрезка
const b = 2; // правая граница отрезка
const epsilon = 0.0001; // требуемая точность
const result = halfDivisionMethod(a, b, f, epsilon);
console.log(result.x); // выведет корень уравнения
console.log(result.iteration); // выведет количество итераций
В результате выполнения примера будет найден корень уравнения и выведено количество итераций, за которые был найден корень с заданной точностью. Для примера с функцией f(x) = x^2 - 4 и отрезком [-2, 2] корень уравнения равен 2 и потребовалось 15 итераций для его нахождения с заданной точностью.
Метод хорд
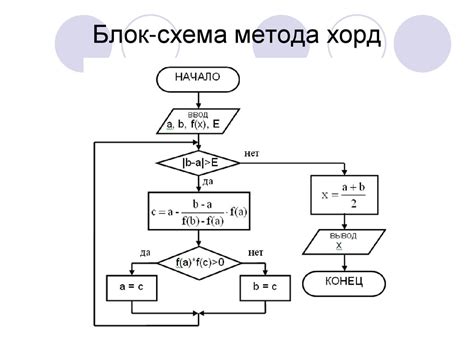
Для применения метода хорд необходимо иметь непрерывную функцию, в которой известны две точки, лежащие на графике этой функции. Одна из точек должна иметь положительное значение функции, а другая - отрицательное. Если взять середину отрезка, соединяющего эти две точки, то полученное значение будет ближе к истинному значению корня уравнения. Операция повторяется до достижения желаемой точности.
Процесс поиска корня уравнения с использованием метода хорд можно представить в виде таблицы. В таблице перечисляются итерационные значения и абсолютные разности между этими значениями и предыдущими.
| № итерации | Левая граница интервала | Правая граница интервала | Текущее значение | Абсолютная разность |
|---|---|---|---|---|
| 1 | x0 | x1 | x2 | |x2 - x1| |
| 2 | x1 | x2 | x3 | |x3 - x2| |
| 3 | x2 | x3 | x4 | |x4 - x3| |
| ... | ... | ... | ... | ... |
Точность результата этого метода зависит от длины начального отрезка и гладкости функции, поэтому метод может потребовать большого количества итераций для достижения нужной точности. Следует также учитывать возможность множественных корней и особенностей функций, которые могут оказать влияние на сходимость метода.
Метод хорд является одним из простейших численных методов и может быть использован для решения большого класса уравнений, однако он не является универсальным решением и может быть неэффективен для некоторых случаев.
Метод касательных
Основные шаги метода касательных:
- Выбор начального приближения x₀.
- Вычисление значения функции f(x₀) и ее производной f'(x₀) в точке x₀.
- Построение касательной к графику функции f(x) в точке x₀.
- Вычисление положения точки пересечения касательной с осью Ox.
- Обновление значения x₀ в соответствии с найденной точкой пересечения касательной.
- Повторение шагов 2-5 до достижения заданной точности.
Для успешного применения метода касательных необходимо выбирать начальное приближение x₀ достаточно близко к искомому корню и обратить внимание на условие сходимости метода.
Пример применения метода касательных для поиска корня уравнения:
- Рассмотрим уравнение f(x) = x² - 4 = 0.
- Выберем начальное приближение x₀ = 2.
- Вычислим значение функции f(x₀) и ее производной f'(x₀) в точке x₀.
- Построим касательную к графику функции f(x) в точке x₀.
- Вычислим положение точки пересечения касательной с осью Ox.
- Обновим значение x₀ в соответствии с найденной точкой пересечения касательной.
- Повторим шаги 3-6 до достижения заданной точности.
Метод касательных широко применяется в численных методах для решения сложных нелинейных уравнений, так как он обеспечивает быструю сходимость и высокую точность результатов.
Примеры применения методов

Ниже приведены несколько примеров применения различных методов для поиска корней уравнения на отрезке:
Метод бисекции (деления отрезка пополам)
Пусть дано уравнение f(x) = 0 и известны две точки на отрезке [a, b], такие что f(a) * f(b) < 0. Используя метод бисекции, можно найти приближенное значение корня уравнения, принадлежащего отрезку [a, b]. Метод заключается в поиске середины отрезка и выборе нового отрезка, внутри которого находится корень. Процесс повторяется до достижения требуемой точности.
Метод Ньютона (касательных)
Метод Ньютона основан на приближении функции касательной в точке и нахождении пересечения касательной с осью абсцисс. Для его применения нужно знать начальное приближение корня уравнения. Метод Ньютона обладает быстрой сходимостью, но требует наличия производной функции.
Метод секущих
Метод секущих аналогичен методу Ньютона, но в данном случае приближение ищется не касательной, а секущей, проходящей через две ближайшие точки на графике функции. Метод секущих может использоваться, если производная функции трудно вычисляется.
Метод простой итерации
Метод простой итерации применяется для нахождения корней уравнения в виде x = g(x), где g(x) - непрерывная функция, причем |g'(x)| n+1 = g(xn). Метод простой итерации сходится к корню, если выполнены определенные условия.
Пример:
Дано уравнение f(x) = x3 - 2x - 5 = 0 на отрезке [1, 3]. Методом бисекции мы можем найти приближенное значение корня, используя начальные точки a = 1 и b = 3. Последовательно деля отрезок пополам и проверяя знак функции в средней точке, мы найдем корень уравнения x ≈ 2.0947.
Пример решения уравнения методом половинного деления
Рассмотрим пример решения уравнения методом половинного деления:
Имеется уравнение: f(x) = x^2 - 4
Требуется найти корень уравнения, принадлежащий отрезку [1, 3].
Шаг 1:
Найдем значения функции f(x) в начальной и конечной точках отрезка:
Начальная точка: f(1) = 1^2 - 4 = -3
Конечная точка: f(3) = 3^2 - 4 = 5
Шаг 2:
Проверим условие наличия корня уравнения на отрезке [a, b]:
Условие выполняется, так как f(a) * f(b) = (-3) * 5 < 0
Шаг 3:
Применим метод половинного деления для поиска корня:
Выберем середину отрезка, которая равна (a + b) / 2 = (1 + 3) / 2 = 2
Вычислим значение функции f(x) в середине отрезка:
f(2) = 2^2 - 4 = 0
Шаг 4:
Проверим условие остановки метода:
Условие выполняется, так как f(2) = 0, т.е. мы нашли корень уравнения.
Таким образом, корень уравнения f(x) = x^2 - 4 на отрезке [1, 3] равен 2.
Пример решения уравнения методом хорд

Шаги решения методом хорд:
- Выбираем начальное приближение x0, которое принадлежит отрезку [a, b].
- Вычисляем значение функции f(x0).
- Находим точку пересечения прямой, проходящей через точки (a, f(a)) и (x0, f(x0)), с осью абсцисс. Это дает нам новое приближение для корня x1.
- Вычисляем значение функции f(x1).
- Повторяем шаги 3 и 4 до тех пор, пока разница между значениями функции на последовательных итерациях не станет достаточно мала.
- Полученное значение x будет приближенным корнем уравнения на отрезке [a, b].
Пример решения уравнения f(x) = x^2 - 4x + 3 методом хорд:
Рассмотрим уравнение f(x) = x^2 - 4x + 3 на отрезке [1, 3].
Найдем первое приближение x0:
| n | x | f(x) |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 3 | 6 |
На основе полученных значений (1, 0) и (3, 6) построим прямую и найдем точку пересечения с осью абсцисс:
| n | x | f(x) |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 3 | 6 |
| - | 2.5 | 0 |
Используя полученное значение x1 = 2.5, вычисляем f(x1):
| n | x | f(x) |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 3 | 6 |
| - | 2.5 | 0 |
| - | - |
Продолжая итерационный процесс, добиваемся достаточной точности:
| n | x | f(x) |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 3 | 6 |
| - | 2.5 | 0 |
| 2 | 1.6667 | -0.3333 |
| 3 | 1.6667 | -0.3333 |
| 4 | 1.6667 | -0.3333 |
Полученное значение x = 1.6667 является приближенным корнем уравнения на отрезке [1, 3].
Пример решения уравнения методом касательных
Рассмотрим пример решения уравнения f(x) = x^3 - 2x - 5 = 0 методом касательных.
Шаг 1: выбор начального приближения. Для примера выберем x₀ = 2.
Шаг 2: вычисление значений функции f(x₀) и её производной f'(x₀) в точке x₀. Для уравнения f(x) = x^3 - 2x - 5 производная равна f'(x) = 3x^2 - 2. Подставим x₀ = 2 и вычислим f(2) и f'(2).
| Итерация | x₀ | f(x₀) | f'(x₀) |
|---|---|---|---|
| 0 | 2 | 1 | 10 |
Шаг 3: вычисление координаты точки пересечения касательной с осью абсцисс. Это можно сделать с помощью формулы x₁ = x₀ - f(x₀) / f'(x₀). Подставим значения из шага 2 и вычислим x₁.
x₁ = 2 - 1 / 10 = 1.9
Шаг 4: проверка условия остановки. Если разница между x₁ и x₀ достаточно мала, то x₁ может быть принято как приближение для корня уравнения. В противном случае, повторить шаги 2-4, используя x₁ в качестве нового приближения.
Полученное значение x₁ = 1.9 можно использовать в качестве приближенного значения корня уравнения f(x) = x^3 - 2x - 5 = 0.
Это был пример решения уравнения методом касательных. Несмотря на итерационный процесс, этот метод обладает достаточно быстрой сходимостью к корню уравнения при выборе хорошего начального приближения.








