Равномощность между множествами - это особое свойство, при котором каждому элементу одного множества сопоставляется уникальный элемент другого множества, и наоборот. Когда два множества являются равномощными, это означает, что они содержат одинаковое количество элементов.
Равномощность является важной концепцией в математике и находит свое применение в различных областях. Она позволяет установить, что два множества имеют одинаковую "вместительность" или "мощность", не вдаваясь в детали их элементов.
Для наглядности понятия равномощности можно использовать пример с равномощностью между множеством студентов и их резюме. Представьте, что у вас есть множество резюме и множество студентов. Если каждому студенту сопоставить резюме, а каждому резюме сопоставить студента, при этом ни одно резюме не будет оставаться без студента, и наоборот, то говорят, что множество студентов и множество резюме являются равномощными.
Равномощность позволяет сравнивать множества различных объектов и находить между ними связи, даже если сами элементы множеств разных типов или имеют разную структуру. Это важный инструмент для анализа и классификации информации в различных дисциплинах.
Мощность множеств: что это такое?

Для конечных множеств мощность вычисляется простым подсчетом элементов. Например, множество {1, 2, 3} имеет мощность 3.
Для бесконечных множеств мощность определяется специальными методами. Один из таких методов - сравнение мощностей различных бесконечных множеств с помощью биекций. Если между двумя бесконечными множествами существует взаимно однозначное соответствие, то их мощности считаются равными.
Также существуют специальные обозначения для мощности множеств. Конечные множества обозначаются символом |A|, где A - само множество. Для бесконечных множеств используются символы aleph (ℵ) и кардиналов.
Знание и понимание мощности множеств является ключевым в теории множеств и математике в целом. Оно позволяет анализировать и сравнивать размеры различных множеств и использовать эту информацию для решения различных задач.
Равномощные множества: определение и примеры
Простым примером равномощных множеств являются множества натуральных чисел и их двойственных. Натуральное число можно сопоставить соответствующему ему двойственному числу: 1 - 0, 2 - 1, 3 - 2 и так далее. Таким образом, множество натуральных чисел и множество их двойственных равномощны.
Еще одним примером равномощных множеств являются множества натуральных чисел и множества целых чисел. Натуральному числу можно сопоставить соответствующее ему целое число: 1 - 0, 2 - 1, 3 - (-1) и так далее. Таким образом, множество натуральных чисел и множество целых чисел равномощны.
| Множество натуральных чисел | Множество двойственных чисел |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 4 |
| ... | ... |
Таким образом, равномощные множества имеют одинаковое количество элементов и могут быть сопоставлены по принципу взаимно однозначного соответствия.
Теория равномощности множеств
В математике концепция равномощности множеств играет важную роль. Два множества считаются равномощными, если между ними существует биекция, то есть такое отображение, которое на каждый элемент одного множества ставит в соответствие уникальный элемент другого множества, и наоборот.
Пусть у нас есть два множества, A и B. Если существует биекция между A и B, то можем записать это как A ≈ B. Например, множества {1, 2, 3} и {a, b, c} равномощны, так как их элементы можно соотнести следующим образом: 1 → a, 2 → b, 3 → c.
Кроме того, отношение равномощности является отношением эквивалентности. Это означает, что оно обладает тремя свойствами:
- Рефлексивность: любое множество равномощно самому себе.
- Симметричность: если A равномощно B, то B равномощно A.
- Транзитивность: если A равномощно B и B равномощно C, то A равномощно C.
Теория равномощности множеств является фундаментальной в математике и находит применение во многих областях, таких как теория множеств, алгебра, топология и другие. Знание и понимание этой концепции позволяет строить математические модели и решать разнообразные задачи, связанные с множествами и их взаимоотношениями.
| Примеры равномощных множеств |
|---|
Множество натуральных чисел N и множество целых чисел Z равномощны. Для каждого натурального числа n можно сопоставить целое число k = 2n, и наоборот, для каждого целого числа k можно найти натуральное число n = k/2. |
Множество действительных чисел R и множество интервалов (0,1) равномощны. Можно установить биекцию между этими множествами, используя функцию f(x) = 1/(1 + e-x). |
Множество всех подмножеств множества A и множество всех бинарных строк равномощны. Каждому подмножеству A можно сопоставить бинарную строку, где i-й бит равен 1, если i-ый элемент принадлежит A, и 0 в противном случае. |
Таким образом, понятие равномощности множеств позволяет сравнивать и классифицировать множества по их размеру и устанавливать взаимосвязи между ними. Оно является одним из фундаментальных понятий теории множеств и имеет широкие применения в различных областях математики и её приложениях.
Доказательство равномощности двух множеств
Доказательство равномощности двух множеств заключается в установлении существования биекции (взаимно однозначного соответствия) между элементами этих множеств.
Пусть имеются два множества A и B. Чтобы доказать, что они равномощны, необходимо построить функцию, которая каждому элементу из A будет ставить в соответствие единственный элемент из B, и наоборот.
Существует несколько способов построения биекции между двумя множествами. Один из них - использование так называемых "пар". Например, если множество A содержит элементы {1, 2, 3}, а множество B элементы {"a", "b", "c"}, то можно установить следующую биекцию: 1 -> "a", 2 -> "b", 3 -> "c". Таким образом, каждый элемент из A соответствует единственному элементу из B, и наоборот.
Другой способ - использование формулы или алгоритма для построения биекции. Например, можно построить биекцию между множеством натуральных чисел и множеством целых чисел, используя формулу f(n) = (-1)^n * (n+1)/2. Эта функция ставит каждому натуральному числу в соответствие единственное целое число, и наоборот.
Важно отметить, что доказательство равномощности двух множеств может быть сложным или требовать математических навыков. Однако в основе каждого доказательства всегда лежит построение взаимно однозначного соответствия между элементами этих множеств.
Канторова теорема о равномощности

Докажем теорему от противного. Предположим, что существует два множества A и B, и мощности этих множеств различны. Без ограничения общности, предположим, что мощность множества A больше мощности множества B.
Тогда существует инъективное отображение f: A ⟶ B, но не существует биективного отображения g: A ⟶ B. Это означает, что у нас есть элементы в множестве A, которые не имеют соответствия в множестве B. Но это противоречит определению инъективного отображения, где каждому элементу из множества A должен соответствовать элемент из множества B.
Следовательно, наше предположение о неравномощности множеств A и B было ошибочным. Существуют бесконечные множества, которые равномощны друг другу.
Одним из самых известных примеров равномощных множеств являются множество натуральных чисел N и множество чётных чисел E. Показано, что существует биективное отображение между этими двумя множествами, что подтверждает равномощность.
Таким образом, канторова теорема о равномощности является важным результатом в математике, позволяющим сравнивать мощности различных бесконечных множеств и решать задачи, связанные с их равномощностью.
Мощность континуума: понятие и свойства
Основное свойство мощности континуума заключается в том, что она больше мощности счетного множества, но строго меньше мощности множества всех подмножеств. Иными словами, существует бесконечное количество действительных чисел, которые нельзя упорядочить в последовательность, но в то же время все действительные числа можно сопоставить с подмножествами натуральных чисел.
Мощность континуума также имеет свойство неразрешимости, что означает, что нельзя однозначно определить, является ли она равной мощности счетного множества или множества всех подмножеств. Это свойство, известное как гипотеза мощности континуума, было предложено Дэвидом Хильбертом в 1900 году и до сих пор остается открытым вопросом.
| Мощность | Количество элементов |
|---|---|
| Счетное множество (N) | Алеф-ноль (ℵ0) |
| Множество всех подмножеств | Алеф-один (ℵ1) |
| Мощность континуума | Алеф-два (ℵ2) |
| ... | ... |
Таким образом, мощность континуума является одной из фундаментальных концепций теории множеств и имеет множество интересных свойств и открытых вопросов, которые продолжают исследоваться математиками до сегодняшнего дня.
Равномощные бесконечные множества

Два бесконечных множества считаются равномощными, если каждому элементу первого множества можно сопоставить уникальный элемент второго множества и наоборот, так чтобы каждый элемент каждого множества был сопоставлен только одному элементу другого множества.
Например, множество всех натуральных чисел {1, 2, 3, ...} и множество всех четных натуральных чисел {2, 4, 6, ...} равномощны, поскольку каждому натуральному числу можно сопоставить удвоенное число. Таким образом, бесконечности этих множеств равны между собой.
Также существует множество других примеров равномощных бесконечных множеств. Например, множество всех целых чисел {..., -3, -2, -1, 0, 1, 2, 3, ...} равномощно множеству всех четных целых чисел {..., -4, -2, 0, 2, 4, ...}.
Равномощность бесконечных множеств отличается от равномощности конечных множеств. Например, множество {1, 2, 3} не равномощно множеству {2, 4, 6}, поскольку для каждого элемента первого множества не существует уникального элемента второго множества, который можно было бы ему сопоставить.
С понятием равномощных бесконечных множеств связано множество философских и математических проблем. Одна из таких проблем - гипотеза Кантора, которая утверждает, что не существует множества, равномощного множеству всех подмножеств натуральных чисел, то есть мощность множества подмножеств натуральных чисел строго больше мощности самого множества натуральных чисел.
Парадокс Хилберта-Троцкого
Парадокс состоит в следующем: предположим, что у нас есть два множества – множество A, состоящее из всех натуральных чисел, и множество B, состоящее из всех четных натуральных чисел. Изначально может показаться, что множество A и множество B имеют разные мощности – множество B является подмножеством множества A, поэтому можно предположить, что они имеют одинаковую или различную мощность. Однако, парадокс в том, что мощность множества B оказывается равной мощности множества A.
Для того чтобы продемонстрировать это, можно построить биекцию между множеством A и множеством B, то есть установить взаимно однозначное соответствие между элементами обоих множеств. Для этого необходимо сопоставить каждому элементу из множества A соответствующий элемент из множества B, например, удвоить каждое число из множества A. Таким образом, каждое число из множества A будет соответствовать какому-то числу из множества B, и наоборот.
Таким образом, парадокс Хилберта-Троцкого показывает, что на первый взгляд различные бесконечные множества могут быть равномощными, то есть иметь одинаковую мощность. Это нарушает нашу интуицию, основанную на работе с конечными множествами, где более объемное множество имеет большую мощность. Множества, имеющие одинаковую мощность, называются равномощными.
Мощность множества всех подмножеств
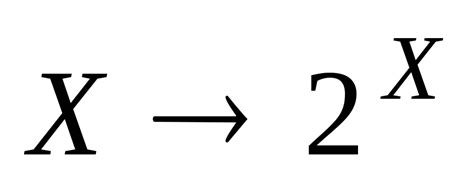
Для примера, рассмотрим множество {1, 2, 3}. В этом случае n равно 3, поэтому мощность множества всех подмножеств будет равна 2 в степени 3, что равно 8.
Мощность множества всех подмножеств можно представить в виде формулы:
Мощность множества всех подмножеств = 2^n
Таким образом, для множества с n элементами мы можем сформировать 2^n различных подмножеств.
Например, для множества {a, b, c} мощность множества всех подмножеств будет равна 2^3 = 8.
Полный набор подмножеств для данного множества будет следующим:
Пустое множество: {}
Множество из одного элемента: {a}, {b}, {c}
Множество из двух элементов: {a, b}, {a, c}, {b, c}
Множество из трех элементов: {a, b, c}
Таким образом, мощность множества всех подмножеств может быть использована для оценки количества возможных комбинаций или вариантов подмножеств для заданного исходного множества.








