Линейная алгебра - одна из важнейших дисциплин математики, которая изучает линейные пространства и операции над ними. Одним из ключевых объектов в линейной алгебре является матрица. Матрицы используются во многих областях, таких как физика, экономика, информатика и многие другие.
Одно из важных понятий, связанных с матрицами, - это линейная зависимость строк матрицы. Линейно зависимые строки матрицы - это такие строки, которые можно выразить как линейную комбинацию других строк матрицы.
Другими словами, если существуют такие коэффициенты, которые не все равны нулю, и при их умножении на соответствующие строки матрицы и их сложении получается строка, равная нулевой строке, то говорят, что строки матрицы линейно зависимы.
Линейно зависимые строки матрицы играют важную роль в решении систем линейных уравнений и нахождении базиса линейного пространства, а также в других линейных операциях. Поэтому понимание и работы с линейно зависимыми строками матрицы очень важно для успешного применения линейной алгебры в практических задачах.
Линейно зависимые строки матрицы: что это такое?

Если строки матрицы являются линейно зависимыми, это означает, что одна из строк является линейной комбинацией других строк. Определение линейной зависимости с помощью матрицы позволяет определить, насколько набор строк является нелинейно зависимым. Если все строки матрицы линейно независимы, то такая матрица называется полным рангом, иначе - неполным рангом.
Проверка линейной зависимости строк матрицы может быть выполнена с помощью элементарных преобразований строк или с использованием метода Гаусса. Если в матрице есть нулевая строка или строка, которая является линейной комбинацией других строк, то строки матрицы линейно зависимы.
Линейно зависимые строки матрицы имеют важное значение в линейной алгебре и теории матриц. Они позволяют определить базисное множество для пространства строк матрицы и исследовать структуру матрицы, ее ранг и размерность пространства строк.
Понятие линейно зависимых строк
Линейно зависимые строки матрицы означают, что существуют такие константы (коэффициенты), при умножении на которые каждая из этих строк может быть представлена в виде линейной комбинации других строк. Формально, строки A1, A2, ..., An называются линейно зависимыми, если существуют не все нули c1, c2, ..., cn, такие что:
c1*A1 + c2*A2 + ... + cn*An = 0
Выражение выше устанавливает линейную зависимость, так как существуют ненулевые коэффициенты c1, c2, ..., cn, при которых сумма всех векторов равна нулевому вектору.
Если все коэффициенты c1, c2, ..., cn равны нулю, то строки считаются линейно независимыми.
Линейно зависимые строки матрицы несут информацию, которая уже присутствует в других строках. Поэтому они могут быть опущены при анализе или решении системы уравнений. В линейной алгебре линейно зависимые строки матрицы могут быть учтены, упрощены или удалены для облегчения вычислений.
Ключевые характеристики линейно зависимых строк

Основные ключевые характеристики линейно зависимых строк:
1. Линейная комбинация: Линейно зависимые строки могут быть выражены как линейная комбинация других строк матрицы. Это означает, что каждая линейно зависимая строка может быть представлена как сумма произведений соответствующих коэффициентов и соответствующих строк матрицы.
2. Ненулевые коэффициенты: В случае линейно зависимых строк, коэффициенты, умножаемые на строки матрицы, не все должны быть равны нулю. По крайней мере один из коэффициентов должен быть ненулевым, чтобы каждая строка была выразима через другие строки.
3. Бесконечное количество решений: Поскольку линейно зависимые строки могут быть выражены как линейная комбинация других строк, существует бесконечное множество решений для системы линейных уравнений, в которой каждая строка представляет собой уравнение. Это означает, что система может иметь бесконечное количество решений.
4. Уменьшение ранга: Если матрица содержит линейно зависимые строки, ее ранг будет меньше, чем количество строк. Ранг матрицы - это максимальное количество линейно независимых строк, которые можно выбрать из матрицы.
Понимание этих ключевых характеристик линейно зависимых строк поможет корректно и эффективно анализировать системы линейных уравнений и решать их.
Практические примеры линейно зависимых строк
Пример 1: Несколько одинаковых строк.
Предположим, у нас есть матрица:
1 2 3 1 2 3 1 2 3В данном случае все три строки матрицы являются одинаковыми и, следовательно, линейно зависимыми. Мы можем выразить одну строку через комбинацию других строк (например, первую строку равна второй строке плюс третьей строке).
Пример 2: Линейно зависимые строки.
Предположим, у нас есть матрица:
1 2 3 2 4 6 3 6 9В данном случае строки матрицы также являются линейно зависимыми. Третья строка, например, может быть выражена как сумма первой и второй строки, умноженных на определенные коэффициенты (третья строка = первая строка + вторая строка).
Пример 3: Матрица с линейно независимыми строками.
Предположим, у нас есть матрица:
1 0 0 0 1 0 0 0 1В данном случае все три строки матрицы являются линейно независимыми, так как ни одну строку нельзя выразить как комбинацию других строк. Они представляют собой базисный векторный набор в пространстве.
Концепция линейно зависимых строк в матрицах имеет важное значение в линейной алгебре и находит применение во многих областях, включая физику, компьютерную графику, машинное обучение и теорию игр.
Матрицы: основные понятия

Одним из важных понятий связанных с матрицами является понятие линейно зависимых строк. Линейно зависимые строки матрицы определяются следующим образом: если существует такой набор коэффициентов, что их линейная комбинация равна нулевому вектору, при этом не все коэффициенты равны нулю, то строки матрицы считаются линейно зависимыми.
Например, рассмотрим следующую матрицу:
$$\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \\
\end{bmatrix} $$
Здесь первая строка матрицы - [1, 2, 3], вторая строка - [4, 5, 6], третья строка - [7, 8, 9]. Если взять коэффициенты a, b и c, такие что $a*[1, 2, 3] + b*[4, 5, 6]+ c*[7, 8, 9] = [0, 0, 0]$, то строки матрицы будут считаться линейно зависимыми.
Линейная независимость строк матрицы означает, что никакая строка из матрицы не может быть выражена в виде линейной комбинации других строк матрицы.
Понятие линейно зависимых и независимых строк имеет важное значение в линейной алгебре и использовывается для решения систем линейных уравнений, вычисления ранга матрицы и в других математических операциях.
Определение матрицы
Матрица может быть представлена в виде MxN, где M – количество строк, а N – количество столбцов. Каждый элемент матрицы указывается его положением в строке и столбце. Обычно элементы матрицы обозначаются буквами в виде aij, где i – номер строки, а j – номер столбца.
Матрицы широко применяются в различных областях математики, физики, программирования и других наук. Они используются для представления систем линейных уравнений, проведения линейных преобразований, решения задач по оптимизации и многих других.
Строки и столбцы матрицы
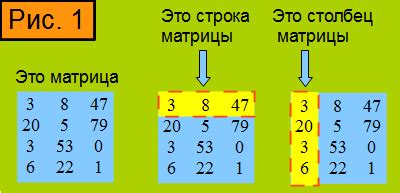
В математике и компьютерных науках матрицы используются для решения различных задач и представления данных. Каждый элемент матрицы обозначается символом aij, где i – номер строки, а j – номер столбца.
Строки и столбцы матрицы имеют различные свойства и могут использоваться для различных целей. Например, строки матрицы могут быть линейно зависимыми или линейно независимыми.
Линейно зависимые строки матрицы – это строки, которые можно представить в виде линейной комбинации других строк. То есть, если существуют такие коэффициенты c1, c2, ..., cn, которые не все равны нулю и сумма c1 A1 + c2 A2 + ... + cn An равна нулевой строке, то строки A1, A2, ..., An линейно зависимы.
На практике, линейная зависимость строк матрицы может иметь различные интерпретации и использоваться для решения различных задач. Например, она может использоваться для определения линейной зависимости или независимости системы уравнений, для нахождения базиса пространства столбцов матрицы и т.д.
Таким образом, понимание свойств строк и столбцов матрицы является важным для работы с матрицами и их применения в различных областях науки и инженерии.
Основные операции с матрицами
Основными операциями с матрицами являются:
- Сложение матриц: при данной операции складываются соответствующие элементы матриц и получается новая матрица, имеющая те же размеры.
- Умножение матрицы на число: каждый элемент матрицы умножается на заданное число.
- Умножение матриц: умножение двух матриц возможно только в случае, если количество столбцов первой матрицы равно количеству строк второй матрицы. Результатом умножения будет новая матрица, в которой элемент на позиции (i, j) есть сумма произведений элементов i-й строки первой матрицы на j-й столбец второй матрицы.
- Транспонирование матрицы: при данной операции строки и столбцы матрицы меняются местами.
Операции над матрицами обладают некоторыми особенностями, такими как коммутативность или дистрибутивность, что позволяет применять их в решении различных математических задач и моделировании процессов.








