Кусочно монотонная функция - это функция, которая обладает свойством монотонности на каждом из своих интервалов. То есть, график функции может иметь участки, где он возрастает или убывает. Каждый интервал может быть как открытым, так и закрытым. Важно отметить, что функция может иметь различные поведения на разных интервалах.
Такая функция может быть определена как набор упорядоченных интервалов, на каждом из которых она монотонна. Для определения кусочно монотонной функции необходимо проанализировать поведение функции на каждом интервале и проверить условие монотонности.
Например, функция может быть кусочно монотонной, если на интервале (a, b) возрастает, на интервале [b, c] убывает, а на интервале (c, d) снова возрастает.
Отличительной особенностью кусочно монотонной функции является то, что она не обязательно является монотонной на всей числовой прямой. Однако, она может быть аппроксимирована набором монотонных функций, каждая из которых определена на своем интервале.
Что такое функция
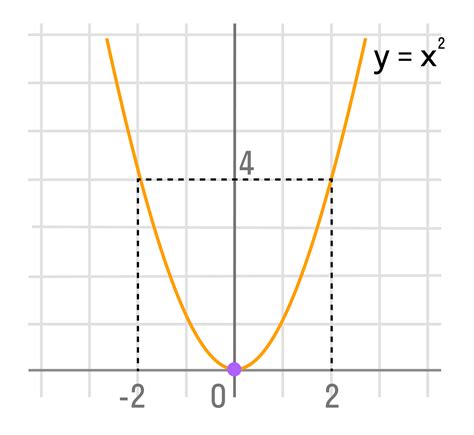
Символическое представление функции заключается в записи выражения, которое определяет соответствие между входящими и исходящими значениями. Обычно функции обозначаются буквами, например, f(x) или g(t). В этом случае переменная (например, x или t) является аргументом функции, а выражение после знака равенства определяет формулу для вычисления значения функции при заданном аргументе. Например, функция f(x) = x^2 определяет соответствие между аргументом x и его квадратом.
Графическое представление функции - это способ визуализации ее значений на плоскости. Значения функции отображаются в виде точек на координатной сетке, где аргумент (обычно обозначенный осью x) находится по горизонтальной оси, а значения функции (обычно обозначенные осью y) находятся по вертикальной оси. Таким образом, график функции позволяет наглядно представить зависимость между аргументом и его значением.
Понятие монотонности функции
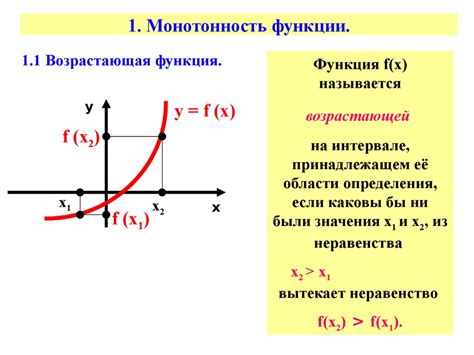
Монотонность функции может быть определена по значению ее производной. Если производная функции всегда положительна, то она является строго возрастающей. Если производная всегда отрицательна, то функция является строго убывающей. Если производная равна нулю, то функция остается постоянной.
Также монотонность функции может быть определена по изменению знака ее разности. Если при увеличении аргумента значение функции всегда увеличивается, то функция является возрастающей. Если значение функции всегда уменьшается при увеличении аргумента, то функция является убывающей.
Знание монотонности функции позволяет анализировать ее поведение и применять соответствующие методы для решения математических задач.
Определение кусочно монотонной функции

Чтобы определить, является ли функция кусочно монотонной, нужно проверить монотонность функции на каждом отрезке, на котором она определена. Если функция монотонна на каждом из этих отрезков, тогда она является кусочно монотонной.
Для проверки монотонности функции можно использовать различные методы, включая вычисление производной, анализ знаков производной или использование графика функции.
Примеры кусочно монотонных функций включают линейные функции, ступенчатые функции и некоторые алгебраические функции.
| Тип функции | Пример | ||
|---|---|---|---|
| Линейная функция | f(x) = 2x + 1 | ||
| Ступенчатая функция | f(x) =
|
Важно отметить, что не все функции являются кусочно монотонными. Например, функция синуса не является кусочно монотонной, поскольку она не монотонна на всем своем интервале определения.
Способы определения кусочно монотонной функции
- Анализ знака производной функции: если производная функции не меняет знак на каждом интервале своей определенности, то функция является кусочно монотонной. Для этого необходимо найти производную функции и рассмотреть знак этой производной на каждом интервале определенности функции.
- Анализ графика функции: график кусочно монотонной функции будет состоять из отдельных монотонных участков, где функция монотонно возрастает или убывает. Для определения положительной монотонности функции рассмотрим ее график и проверим, что график на каждом участке возрастает или не убывает. Аналогично для отрицательной монотонности.
- Изучение интервалов монотонности: функция может иметь определенные точки разрыва или экстремумов, которые могут нарушать монотонность. Для этого необходимо найти все точки разрыва и экстремумы функции, а затем изучить знак функции на каждом интервале между этими точками.
Используя эти способы, можно определить, является ли функция кусочно монотонной и на каких интервалах она монотонна.
Примеры кусочно монотонных функций
Примером кусочно монотонной функции является функция, заданная следующим образом:
f(x) = x2 для x ≤ 0
f(x) = 2x для 0
f(x) = -x для x > 2
В данном примере функция f(x) разделена на три части: отрицательные значения x, интервал (0, 2] и положительные значения x. В каждой части функция либо монотонно возрастает, либо монотонно убывает.
Другим примером кусочно монотонной функции является функция, заданная следующим образом:
f(x) = 3x для x ≤ 1
f(x) = x2 для 1
f(x) = 2 для x > 2
В данном примере функция f(x) разделена на три части: значения x, меньшие или равные 1, интервал (1, 2] и значения x, большие 2. В каждой части функция либо монотонно возрастает, либо монотонно убывает.
Таким образом, кусочно монотонные функции представляют собой интересный и полезный класс функций, который имеет свои особенности и применение в различных областях математики и естественных наук.








