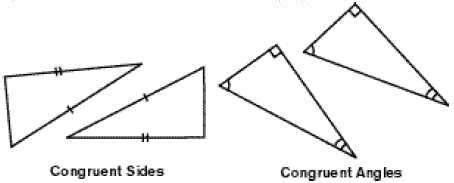
Конгруэнтные треугольники - это треугольники, которые имеют одинаковые стороны и углы. В геометрии конгруэнтность является одним из основных понятий, позволяющих сравнивать и классифицировать геометрические фигуры. Конгруэнтность треугольников означает, что они полностью совпадают после перемещений, поворотов и зеркальных отражений.
Для двух треугольников A и B существует несколько способов показать их конгруэнтность. Например, совпадение всех трех сторон, совпадение двух сторон и между ними одного угла, или совпадение двух углов и между ними одной стороны. Изучение конгруэнтных треугольников позволяет делать выводы о равенстве и соотношении их сторон и углов.
Конгруэнтные треугольники обладают рядом свойств, на которых основано их сравнение и классификация. Например, если две стороны их трех равными сторонами одних из трех конгруэнтных треугольников, то третьи стороны также равны. Также, сумма двух конгруэнтных углов равна третьему углу, и т. д.
Примечание: Знание конгруэнтных треугольников имеет практическое применение в различных областях, включая архитектуру, инженерное дело и компьютерную графику. Также, изучение конгруэнтных треугольников является важным этапом в обучении геометрии и математики в целом.
Определение конгруэнтных треугольников
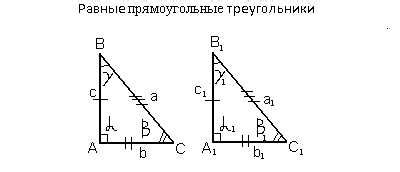
Для простого понимания конгруэнтности треугольников существуют три способа определения их равенства:
- Сторона-сторона-сторона (С-С-С): Если в двух треугольниках все соответствующие стороны равны, то треугольники конгруэнтны.
- Угол-сторона-угол (У-С-У): Если в двух треугольниках два соответствующих угла и сторона между ними равны, то треугольники конгруэнтны.
- Угол-угол-сторона (У-У-С): Если в двух треугольниках два соответствующих угла и сторона, не являющаяся стороной между ними, равны, то треугольники конгруэнтны.
Конгруэнтные треугольники имеют одинаковую форму и размеры, поэтому все их стороны и углы равны между собой. Это понятие является важным в геометрии и на практике используется для решения задач, связанных с построением и измерением треугольников.
Свойства конгруэнтных треугольников
1. Теорема о равенстве сторон и углов: Если два треугольника имеют соответствующие равные стороны и углы, то они конгруэнтны. Это свойство позволяет определить конгруэнтные треугольники по их сторонам и углам.
2. Закон синусов: Если в треугольнике известны две стороны и угол между ними, то третья сторона может быть найдена с помощью закона синусов. Для конгруэнтных треугольников этот закон также справедлив, что позволяет определить отсутствующие стороны в конгруэнтных треугольниках.
3. Теорема о гомотетии: Если два треугольника конгруэнтны, то они могут быть получены друг из друга с помощью гомотетии – геометрического преобразования, при котором все точки фигуры увеличиваются или уменьшаются в одно и то же количество раз.
4. Сумма углов в треугольнике: Все треугольники, включая конгруэнтные, обладают свойством, что сумма всех его внутренних углов равна 180 градусам. Это утверждение называется теоремой о сумме углов треугольника и может быть использовано для доказательства конгруэнтности треугольников.
5. Теорема о равных углах: Если два треугольника конгруэнтны, то соответствующие углы в них равны.
Благодаря этим свойствам, конгруэнтные треугольники могут быть полностью определены и изучены. Они широко используются в геометрических и математических рассуждениях, а также в практических приложениях, связанных с построением и анализом треугольников.
Критерии конгруэнтности
Два треугольника считаются конгруэнтными, если они имеют одинаковые стороны и одинаковые углы. Существует несколько критериев, с помощью которых можно определить конгруэнтность треугольников.
1. Критерий по трем сторонам (ССС): если все стороны одного треугольника равны соответственно сторонам другого треугольника, то эти треугольники конгруэнтны.
| Треугольник ABC | Треугольник DEF | |
|---|---|---|
| AB = DE | BC = EF | AC = DF |
2. Критерий по двум сторонам и включенному углу (СУУ): если две стороны одного треугольника равны соответственно двум сторонам другого треугольника и включенные между ними углы также равны, то эти треугольники конгруэнтны.
| Треугольник ABC | Треугольник DEF | |
|---|---|---|
| AB = DE | BC = EF | ∠ABC = ∠DEF |
3. Критерий по двум углам и включенной стороне (УУС): если два угла одного треугольника равны соответственно двум углам другого треугольника и включенная между ними сторона также равна, то эти треугольники конгруэнтны.
| Треугольник ABC | Треугольник DEF | |
|---|---|---|
| ∠ABC = ∠DEF | ∠BCA = ∠EFD | AC = DF |
Используя эти критерии, можно определить конгруэнтность треугольников и решать геометрические задачи с их применением.
Треугольные неравенства и конгруэнтные треугольники
Рассмотрим треугольник ABC. Если сторона AB больше стороны AC и сторона BC больше стороны AC, то можно сделать вывод, что угол BAC будет наименьшим углом треугольника ABC. Аналогично, если сторона AB меньше стороны AC и сторона BC меньше стороны AC, то угол BAC будет наибольшим углом треугольника ABC.
Конгруэнтные треугольники – это треугольники, которые имеют одинаковые стороны и одинаковые углы. Если два треугольника имеют равные стороны и равные углы, то они считаются конгруэнтными. Конгруэнтные треугольники обладают множеством свойств и признаков, которые могут быть использованы для решения различных геометрических задач и построений.
- Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то эти треугольники конгруэнтны.
- Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то эти треугольники конгруэнтны.
- Если все три стороны одного треугольника равны соответственно всем трем сторонам другого треугольника, то эти треугольники конгруэнтны.
- Если две стороны и угол, не входящий между ними, одного треугольника равны соответственно двум сторонам и углу, не входящему между ними, другого треугольника, то эти треугольники конгруэнтны.
Используя свойства конгруэнтных треугольников, можно решать задачи на нахождение недостающих сторон и углов треугольника, а также проводить различные построения в геометрии.
Классификация конгруэнтных треугольников
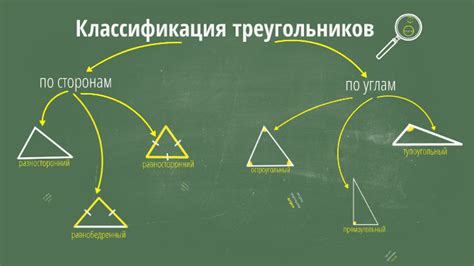
Конгруэнтные треугольники могут быть классифицированы на основе своих свойств и характеристик. Вот некоторые из наиболее распространенных классификаций:
1. По длинам сторон:
Треугольники, у которых все стороны равны, называются равносторонними треугольниками.
Треугольники, у которых две стороны равны, называются равнобедренными треугольниками.
Треугольники, у которых все стороны разные, называются разносторонними треугольниками.
2. По величине углов:
Треугольники, у которых все углы прямые (равны 90 градусам), называются прямоугольными треугольниками.
Треугольники, у которых один угол равен 90 градусам, называются прямоугольными треугольниками. В этом случае другие два угла являются острыми.
3. По соотношению сторон и углов:
Треугольники, у которых все стороны и углы равны, называются равносторонними и равноугольными треугольниками. В таких треугольниках они все прямые.
Треугольники, у которых две стороны и два угла равны, называются равносторонними и равноугольными треугольниками. В таких треугольниках один угол может быть прямым, а другие два - острыми.
Треугольники, у которых все стороны разные, но два угла равны, называются равнобедренными и равноугольными треугольниками.
Знание этих классификаций позволяет более глубоко изучать свойства конгруэнтных треугольников и использовать их в решении геометрических задач.
Конгруэнтные треугольники и их взаимодействие с окружностями
Взаимодействие конгруэнтных треугольников с окружностями также представляет большой интерес. Окружность - это множество точек, которые находятся на одинаковом расстоянии от центра окружности. У конгруэнтных треугольников есть несколько основных свойств, связанных с окружностями:
| Свойство | Описание |
|---|---|
| Серединный перпендикуляр | Для каждой стороны конгруэнтного треугольника существует окружность, ортогональная этой стороне и проходящая через середину этой стороны. |
| Биссектриса угла | Для каждого угла конгруэнтного треугольника существует окружность, делящая этот угол пополам. |
| Описанная окружность | Описанная окружность - это окружность, проходящая через все вершины конгруэнтного треугольника. |
Использование окружностей позволяет получить различные свойства и следствия для конгруэнтных треугольников. Например, через любые три точки, лежащие на описанной окружности, можно провести еще одну окружность, которая будет касаться внутренностей сторон треугольника. Также, зная радиус описанной окружности, можно выразить площадь конгруэнтного треугольника через формулу S = R^2 * sin(A) * sin(B) * sin(C), где S - площадь треугольника, R - радиус описанной окружности, A, B, C - углы треугольника.
Кординаты вершин конгруэнтных треугольников
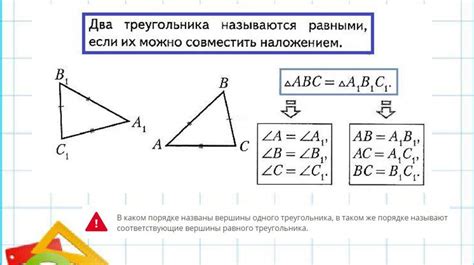
Для определения конгруэнтных треугольников по заданным точкам на плоскости требуется знание координат вершин каждого треугольника. Координаты вершин можно определить с помощью геометрических методов и формул, которые связывают точки с числовыми значениями.
Пусть даны два треугольника: ABC и DEF. Координаты вершин треугольника ABC обозначим как (x1, y1), (x2, y2) и (x3, y3), а координаты вершин треугольника DEF - как (x4, y4), (x5, y5) и (x6, y6).
Существуют несколько способов определения координат вершин конгруэнтных треугольников:
1. Геометрический метод. Если известны длины сторон треугольников и их углы, можно использовать тригонометрические функции для определения координат вершин. Например, для определения координат вершины C треугольника ABC можно использовать следующую формулу:
x3 = x1 + AC * cos(C)
y3 = y1 + AC * sin(C)
2. Аналитический метод. Если известны координаты вершин одного треугольника и вектор перемещения от него к другому треугольнику, можно вычислить координаты вершин второго треугольника. Например, если вектор перемещения от треугольника ABC к DEF - это вектор (dx, dy), то можно использовать следующие формулы для определения координат вершин треугольника DEF:
x4 = x1 + dx
y4 = y1 + dy
x5 = x2 + dx
y5 = y2 + dy
x6 = x3 + dx
y6 = y3 + dy
Координаты вершин треугольников могут быть использованы для вычисления других параметров, таких как площадь, периметр, высоты и т.д. Эти параметры могут быть полезными при решении геометрических задач или анализе свойств конгруэнтных треугольников.
| Вершины треугольника ABC | Вершины треугольника DEF |
|---|---|
| (x1, y1) | (x4, y4) |
| (x2, y2) | (x5, y5) |
| (x3, y3) | (x6, y6) |
Существование и единственность конгруэнтных треугольников
Существование конгруэнтных треугольников зависит от условий, заданных в соответствующей задаче или теореме. Если вместе с треугольником заданы определенные условия на стороны или углы, то существует ровно один конгруэнтный треугольник, удовлетворяющий этим условиям.
Например, если два треугольника имеют две соответствующие стороны и угол между ними равными, то они являются конгруэнтными. Это свойство называется "СКС" (сторона-катет-сторона). Также существуют другие свойства, позволяющие определить конгруэнтность треугольников, например, "СС" (сторона-сторона) или "УУ" (угол-угол).
Теорема о существовании единственности конгруэнтных треугольников гласит, что если у двух треугольников равны все соответствующие стороны и углы, то они совпадают. Другими словами, конгруэнтные треугольники единственны.
Конгруэнтные треугольники и их связь с площадью
Конгруэнтные треугольники имеют ряд свойств, влияющих на их площадь:
- Если два треугольника конгруэнтны, то их площади равны.
- Площадь треугольника зависит только от длин его сторон и угла между ними.
- Если два треугольника равны по площади, то они конгруэнтны.
- Если два треугольника имеют одну общую сторону и равные площади, то они конгруэнтны.
- Если два треугольника имеют равные стороны и равные углы, то они конгруэнтны.
- Площадь треугольника можно вычислить по формуле Герона, используя длины его сторон.
Таким образом, связь между конгруэнтными треугольниками и их площадью позволяет нам устанавливать равенство площадей треугольников и применять различные методы для вычисления площади треугольника.
Некоторые задачи на конгруэнтные треугольники
Конгруэнтные треугольники широко используются в различных задачах геометрии. Ниже приведены некоторые примеры задач, связанных с конгруэнтными треугольниками.
- Задача 1: Даны два треугольника ABC и DEF. Если стороны треугольника ABC соответственно равны сторонам треугольника DEF, и углы ABC и DEF соответственно равны углам DEF и ABC, то треугольники ABC и DEF являются конгруэнтными.
- Задача 2: Даны два треугольника PQR и STU. Если две стороны треугольника PQR соответственно равны двум сторонам треугольника STU, и содержащиеся между этими сторонами углы равны, то треугольники PQR и STU являются конгруэнтными.
- Задача 3: Даны два треугольника XYZ и MNO. Если две стороны треугольника XYZ соответственно равны двум сторонам треугольника MNO, и угол между этими сторонами равен углу между соответствующими сторонами треугольника MNO, то треугольники XYZ и MNO являются конгруэнтными.
- Задача 4: Даны два треугольника ABC и DEF. Если две стороны треугольника ABC соответственно равны двум сторонам треугольника DEF, и угол между этими сторонами прямой, то треугольники ABC и DEF являются конгруэнтными. Эта задача особенно важна, так как позволяет доказать конгруэнтность треугольников, используя только условие равенства двух сторон и прямого угла.
Выполнение этих задач позволяет более глубоко изучить свойства конгруэнтных треугольников и применить их в решении сложных геометрических задач.








