В математике и физике, компланарные векторы играют важную роль при решении различных задач. Компланарные векторы - это векторы, лежащие в одной плоскости. Такая плоскость может быть определена двумя или более векторами.
Одним из важных свойств компланарных векторов является возможность их линейной комбинации. Это означает, что любой вектор, лежащий в той же плоскости, может быть представлен в виде суммы или разности других векторов, также лежащих в этой плоскости.
Применение компланарных векторов широко распространено в различных областях науки. Например, в механике компланарные векторы используются для моделирования движения тела в плоскости. С помощью компланарных векторов можно определить скорость и ускорение тела в определенный момент времени.
Компланарные векторы также находят применение в физике жидкостей и газов, где они используются для описания потоков и распределения величин, таких как давление и температура.
В геометрии компланарные векторы позволяют определить линейные зависимости между точками в пространстве, а также рассчитать площадь и объем фигур, образованных этими векторами.
Таким образом, понимание и использование компланарных векторов является важным инструментом для решения различных задач в науке и технике.
Векторы в трехмерном пространстве
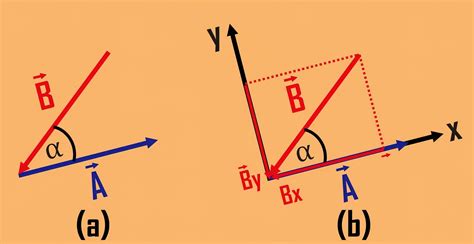
Векторы в трехмерном пространстве описываются с помощью трех координат или компонент вектора. Каждая компонента представляет собой значение вектора по соответствующей оси x, y и z. Таким образом, вектор в трехмерном пространстве имеет вид:
В = (x, y, z)
где x, y и z - координаты вектора по оси x, y и z соответственно.
Векторы в трехмерном пространстве могут быть компланарными, то есть находиться в одной плоскости. Компланарные векторы лежат на одной плоскости и могут быть использованы для решения различных задач и проблем, включая задачи геометрии, физики и инженерии.
Компланарные векторы могут быть найдены с помощью различных методов и алгоритмов. Один из способов - это использование определителя матрицы, построенной на компонентах векторов. Если определитель равен нулю, то векторы компланарны. Если определитель не равен нулю, то векторы не компланарны и лежат в разных плоскостях.
Применение компланарных векторов включает решение задач трехмерной геометрии, нахождение площадей и объемов фигур, анализ движений в пространстве, определение направлений сил и моментов в физических системах и многое другое. Компланарные векторы имеют важное значение во многих областях науки и техники.
Определение компланарности векторов
Чтобы определить компланарность векторов, нужно проанализировать их линейную независимость. Векторы a, b и c называются компланарными, если существуют такие числа x, y и z, что выполнено равенство:
x * a + y * b + z * c = 0
Если уравнение выше имеет нетривиальное решение (т.е. x, y и z не все равны нулю), то это означает, что векторы a, b и c компланарны.
Компланарные векторы имеют множество применений в различных областях. Например, в физике компланарные силы позволяют анализировать равновесие тела, а в геометрии компланарные векторы используются при построении трехмерной модели объектов.
Таким образом, понимание компланарности векторов является важным для успешного решения задач, связанных с трехмерным пространством и его приложениями.
Свойства компланарных векторов

- Сложение компланарных векторов. Компланарные векторы могут складываться и вычитаться друг из друга. Результатом сложения компланарных векторов является новый вектор, который также будет лежать в той же плоскости.
- Линейная зависимость компланарных векторов. Если компланарные векторы линейно зависимы, то они могут быть представлены в виде линейной комбинации друг друга. Это значит, что один из векторов можно выразить через другие с помощью умножения на коэффициенты и сложения.
- Линейная независимость компланарных векторов. Если компланарные векторы линейно независимы, то они не могут быть представлены в виде линейной комбинации друг друга. Каждый вектор имеет свою уникальную роль и не может быть выражен через остальные.
- Скалярное произведение компланарных векторов. Скалярное произведение компланарных векторов равно произведению модулей векторов на косинус угла между ними. Если два вектора компланарны, то их скалярное произведение равно нулю.
- Векторное произведение компланарных векторов. Векторное произведение компланарных векторов равно нулю, так как оно перпендикулярно плоскости, в которой лежат векторы.
Свойства компланарных векторов играют важную роль в различных областях науки и техники, таких как физика, геометрия, механика и др. Они позволяют анализировать и решать разнообразные задачи, связанные с плоскими структурами и движением объектов.
Общее уравнение компланарности
Общее уравнение компланарности имеет вид:
[x, y, z] * [a, b, c] = d
где [x, y, z] – координаты вектора, [a, b, c] – координаты другого вектора, а d – константа.
Для проверки компланарности двух векторов необходимо подставить их координаты в уравнение и сравнить полученный результат с константой. Если они равны, значит, векторы компланарны, иначе – нет.
Общее уравнение компланарности широко применяется в геометрии, физике и инженерии. Например, оно используется при решении задач на нахождение плоскости, проходящей через заданные точки или параллельной заданным векторам.
Геометрическая интерпретация компланарности

Одной из основных геометрических интерпретаций компланарных векторов является возможность построения плоскости, содержащей все эти векторы. Для этого необходимо выбрать любые два неколлинеарных (не лежащих на одной прямой) вектора в данном множестве компланарных векторов и найти их векторное произведение. Это векторное произведение будет нормалью к плоскости, содержащей все эти векторы. Таким образом, можно определить уравнение плоскости.
Использование компланарных векторов и геометрической интерпретации компланарности имеет множество применений. Например, векторы, описывающие силы на тело, могут быть компланарными векторами. Зная векторное произведение таких векторов, можно определить момент силы на тело и его направление. Это дает возможность более точно анализировать и предсказывать поведение тела под воздействием сил.
Также компланарные векторы используются в геометрии при решении задач на планиметрию, в топологии, механике, электродинамике и многих других областях науки и техники. Знание и понимание компланарности векторов позволяет решать сложные задачи, связанные с трехмерным пространством и его свойствами.
| Пример | Иллюстрация |
|---|---|
| Векторное произведение компланарных векторов |  |
Проекция компланарных векторов на плоскость
Проекция вектора на плоскость представляет собой процесс нахождения компонентов вектора, которые лежат в данной плоскости. Для этого можно использовать проекцию вектора на каждую из осей плоскости, а затем суммировать полученные компоненты.
Проекция компланарных векторов на плоскость может использоваться для решения различных задач. Например, в физике проекция векторов на плоскость может помочь определить компоненты вектора силы, действующие в горизонтальной и вертикальной плоскостях. В графике и компьютерной графике проекция векторов на плоскость часто используется для определения положения объектов на экране и расчета их движения.
Векторная проекция на плоскость имеет формулу, основанную на проекциях на канонические базисные векторы плоскости:
Проекция вектора a на плоскость можно найти по формуле:
- Проекция a на ось Х: ax = a * ex;
- Проекция a на ось Y: ay = a * ey;
Затем можно получить компоненты ax и ay, которые лежат в плоскости, путем сложения проекций на оси.
Этот подход позволяет эффективно работать с компланарными векторами и использовать их в различных задачах, связанных с анализом и моделированием трехмерных объектов.








