Кардинальное число - это математическое понятие, которое используется для определения количества элементов во множестве или для установления соответствия между двумя множествами. Оно говорит о том, сколько элементов имеется в множестве, и является одним из основных понятий теории множеств. Кардинальное число является способом измерения количественных характеристик объектов в математике.
Значение кардинального числа зависит от контекста его использования. В теории множеств, кардинальное число указывает на количество элементов, содержащихся в данном множестве. Например, множество целых чисел от 1 до 10 содержит 10 элементов, поэтому его кардинальное число равно 10.
Однако, в других областях математики и науки, кардинальные числа могут иметь особое значение или назначение. Например, в теории вероятностей, кардинальное число может указывать на вероятность возникновения определенного события. В физике, кардинальные числа могут иметь значения, связанные с физическими параметрами, такими как скорость, масса или энергия.
Важно отметить, что кардинальные числа могут быть как конечными, так и бесконечными. Например, множество всех натуральных чисел имеет бесконечное количество элементов, поэтому его кардинальное число равно бесконечности.
Кардинальные числа являются фундаментальным понятием в математике и имеют широкое применение в различных областях науки. Они позволяют выражать количественные характеристики объектов и проводить анализ и исследования в различных математических и научных дисциплинах.
Что такое кардинальное число?
В теории множеств кардинальные числа используются для сравнения размерности различных множеств и определения их равномощности. Два множества считаются равномощными, если между ними существует биективное отображение, то есть каждому элементу одного множества ставится в соответствие уникальный элемент другого множества.
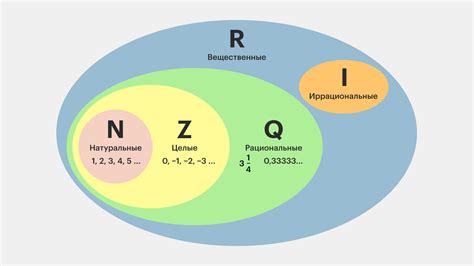
Однако, не все кардинальные числа могут быть сравнимы между собой. Так, существует такое понятие как континуум-гипотеза, которая гласит о том, что между кардинальными числами N (натуральные числа) и R (все вещественные числа) не существует промежуточных кардинальных чисел.
Кардинальные числа играют важную роль в математике, особенно в теории множеств и анализе. Они позволяют рассматривать различные способы изучения размерности и мощности множеств, что имеет большое значение при решении различных математических задач и проблем.
Значение и определение
Кардинальным числом называется число, которое используется для определения количества элементов в некотором множестве. Основная особенность кардинальных чисел заключается в том, что они не зависят от порядка элементов в множестве и от способа представления множества.
Определение кардинальных чисел было введено в математическую теорию множеств и является основным понятием в этой области. Кардинальность множества обозначается символом |A|, где A – множество. Кардинальные числа могут быть конечными или бесконечными.
В математике существует несколько способов определения конкретного кардинального числа, таких как натуральные числа, целые числа, рациональные числа и вещественные числа. Все эти числа используются для обозначения конкретных мощностей (количеств) множеств.
Кардинальные числа являются важными для решения многих математических задач и играют значительную роль в различных областях науки, таких как теория вероятности, анализ данных, теория множеств и др.
Определение и изучение кардинальных чисел является одной из основ математики и имеет широкий спектр применений в различных дисциплинах. Понимание значения кардинальных чисел позволяет более глубоко понять и анализировать различные явления и процессы с точки зрения количественных характеристик и их взаимосвязей.
Примеры использования кардинальных чисел

Кардинальные числа широко используются в математике и науке для измерения и определения количественных характеристик. Вот несколько примеров их использования:
- Количество элементов во множестве: Кардинальное число используется для определения количества элементов во множестве, например, количество студентов в классе или количество планет в солнечной системе.
- Мощность множества: Кардинальное число также используется для определения мощности множества, то есть количества всех возможных элементов в множестве. Например, мощность множества всех натуральных чисел является бесконечной кардинальной числом, обозначаемой символом ∞.
- Вероятность события: Кардинальное число может быть использовано для определения вероятности события. Например, вероятность выпадения определенной карты из колоды может быть определена как отношение числа одинаковых карт к общему числу карт в колоде.
- Размерность векторного пространства: В линейной алгебре, размерность векторного пространства может быть определена с помощью кардинального числа. Например, размерность трехмерного векторного пространства будет равна трем.
Это лишь некоторые примеры использования кардинальных чисел в различных областях знаний. Кардинальные числа играют важную роль в математике и науке, помогая нам измерять и характеризовать количественные характеристики объектов и явлений.
Важность кардинальных чисел в математике
Во-первых, кардинальные числа используются для сравнения размеров различных множеств. С помощью понятия кардинальности можно определить, одинаково ли мощны два множества или одно множество мощнее другого. Например, можно определить, имеют ли множества натуральных чисел и рациональных чисел одинаковую мощность, и установить, что оба этих множества счетные.
Во-вторых, кардинальные числа используются для изучения бесконечных множеств. Они позволяют классифицировать множества на счетные и несчетные, что имеет важное значение в различных областях математики, таких как теория множеств, топология и анализ.
Также кардинальные числа важны для понимания конечных и бесконечных действительных чисел. Каждое действительное число может быть представлено с помощью кардинального числа, которое указывает на его позицию на числовой прямой. Это позволяет более точно описывать и анализировать величины и их отношения в математике и других науках.
Таким образом, кардинальные числа являются важным инструментом для изучения и анализа множеств различных размерностей и их свойств. Они помогают строить систематические абстракции, которые служат основой для различных областей математики и науки в целом.








